Теорема чевы

Доказательство

Доказательство теоремы Пифагора, используя алгебру

Нужно доказать, что c² = a² + b²:

Это квадрат, в котором есть 4 одинаковых треугольника abc:

1. Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
2. Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
3. Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
4. Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
5. Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:

(a + b) (a + b) = c² + 2ab

a² + 2ab + b² = c² + 2ab

a² + b² = c²

Что и требовалось доказать.

«Пифагоровы штаны на все стороны равны»

Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора

На этой фигуре c — гипотенуза, a и b — катеты.

Проведём перпендикулярную линию к гипотенузе (c):

Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).

1. Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
2. Делим «Пифагоровы штаны» на 3 похожие фигуры:
3. Все 3 треугольника подобны друг другу (A, B, C) и из-за этого «фигуры-домики» также являются подобными.
4. Значит соотношение площади A и a² будет одинаковым с площадью B и b², но и с площадью C и c². Т. е.: A/a² = B/b² = C/c² = β (назовём это соотношение греческой буквой бета);
5. Площадь каждого треугольника, через площадь каждого из квадратов, равна: A = βa², B = βb², C = βc²;
6. Вспомним, что С = А + B, т. е. βc² = βa² + βb², это равно c² = a² + b².

Что и требовалось доказать.

утверждение

Две линии (черного цвета), которые пересекаются со стороной треугольника внутри и пересекаются с другими сторонами внутри и снаружи

Аксиома утверждает, что,

Аксиома Паша  —  Пусть A, B, C — три точки, которые не лежат на прямой, и пусть a — прямая на плоскости ABC, которая не пересекает ни одну из точек A, B, C. Если прямая a проходит через a точки отрезка AB, он также проходит через точку отрезка AC или через точку отрезка BC.

Тот факт, что отрезки AC и BC не пересекаются прямой a , доказан в Приложении I, 1, написанном П. Бернейсом .

Более современная версия этой аксиомы выглядит следующим образом:

Более современная версия аксиомы Паша  —  на плоскости , если линия пересекает одну сторону треугольника внутри, то она пересекает ровно одну другую сторону внутри и третью сторону снаружи , если она не проходит через вершину треугольника.

(В случае, если третья сторона параллельна нашей линии, мы считаем «пересечение на бесконечности» внешним.) Часто встречается более неформальная версия аксиомы:

Более неформальная версия аксиомы паша  —  Если линия, не проходящая через любую вершину треугольника, встречает одну стороны треугольника , то он встречает другую сторону.

Примеры решения задач

Задача 1

В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.

Решение

По теореме Пифагора ВС2+АС2=АВ2, значит

\(АС\;=\;\sqrt{АВ^2\;-\;АС^2}\)

Для нахождения ответа подставим в формулу исходные значения:

\(АС\;=\;\sqrt{85^2\;-\;36^2}\;=\;\sqrt{7225\;-\;1296\;}={\;\sqrt{5929}\;=\;77\;}\)

Задача 2

Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.

Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:

• 46²+56²= 5252;
• 76²= 5776;
• 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.

Задача 3.

Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.

Решение

Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.

По теореме Пифагора:

АО2+BO2=AB2, значит

Доказуемость и теорема

Чтобы утверждать математическое утверждение как теорему, требуется доказательство. То есть должна быть продемонстрирована правильная линия рассуждений от аксиом и других уже установленных теорем к данному утверждению. В общем, доказательство считается отдельным от самого утверждения теоремы. Частично это связано с тем, что, хотя для одной теоремы может быть известно более одного доказательства, требуется только одно доказательство, чтобы установить статус утверждения как теоремы. Теорема Пифагора и закон квадратичной взаимности претендуют на звание теоремы с наибольшим количеством различных доказательств.

Примеры[править]

Примеры задачправить

Пример 1править

Пусть задано такое рекуррентное соотношение:

Заметим, что , для любого , что удовлетворяет 1 условию. Тогда , где , при

Пример 2править

Задано такое соотношение:

Данное соотношение подходит под первый случай , поэтому его асимптотика совпадает с асимптотикой .

Недопустимые соотношенияправить

Рассмотрим пару соотношений, которые нельзя решить мастер-теоремой:

• не является константой; количество подзадач может меняться,

• рассмотрим , тогда не существует такого , что , так как при , а ограничено,

• , однако пример можно решить следующим образом: заметим, что на шаге, размер , тогда, оценивая сумму, получаем, что ,

• , при составлении асимптотического решения перед каждый раз будет новый знак, что противоречит мастер-теореме.

Алгоритм	Рекуррентное соотношение	Время работы	Комментарий
Целочисленный двоичный поиск			По мастер-теореме , где
Обход бинарного дерева			По мастер-теореме , где
Сортировка слиянием			По мастер-теореме , где

Заявление

Аксиома заявляет это,

:Let A, B, C быть три пункта, которые не лежат на линии и позволяют быть линией в ABC самолета, которая не встречает ни одного из пунктов A, B, C. Если линия проходы через пункт сегмента AB, это также проходит через пункт сегмента AC, или через пункт сегмента до н.э

Факт, что оба сегмента AC и до н.э не пересечены линией доказанного в Приложении I, 1, которое было написано П. Бернейсом.

Более современная версия этой аксиомы следующие:

:In самолет, если линия пересекает одну сторону треугольника внутренне тогда, это пересекает точно одну другую сторону внутренне и третью сторону внешне, если это не проходит через вершину треугольника.

(В случае, если третья сторона параллельна нашей линии, мы считаем «пересечение в бесконечности» как внешнее.) Более неофициальная версия аксиомы часто замечается:

:If линия, не проходя ни через какую вершину треугольника, встречает одну сторону треугольника тогда, это встречает другую сторону.

Другие способы доказательства теоремы

Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.

Методом площадей

Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:

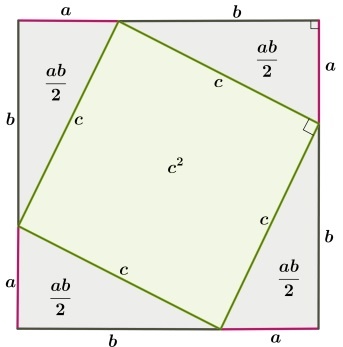
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.

Площадь внешнего квадрата включает в себя:

• сумму площадей четырех прямоугольных треугольников;
• площадь внутреннего квадрата.

Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.

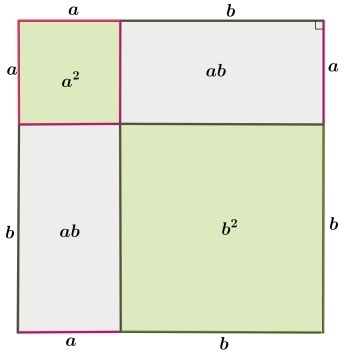
Значит:

4ab2=2ab ⇒ c2=a2+b2, что и нужно было доказать.

Методом бесконечных малых

Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.

В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем

da/ca = c/a, b = const

Разделяя переменные составляется дифференциальное уравнение:

c x dc = a x da

Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:

c2 = a2 + const

определяя из начальных условий константу интегрирования, получим:

a = 0 ⇒ c2 = b2 = const

Таким образом мы определяем, что

c2 = a2 + b2

Теорема доказана!

Обратная теорема Виета

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Она формулируется так:

Обратная теорема Виета Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x2 + bx + c = 0.

Обратные теоремы зачастую сформулированы так, что их утверждением является заключение первой теоремы. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это является утверждением.

Связь с научными теориями

Теоремы в математике и теории в науке принципиально отличаются по своей эпистемологии . Научная теория не может быть доказана; её ключевой атрибут заключается в том, что он фальсифицируется, то есть он делает предсказания о мире природы, которые можно проверить экспериментально . Любое несоответствие между предсказанием и экспериментом демонстрирует неверность научной теории или, по крайней мере, ограничивает её точность или область действия. Математические теоремы, с другой стороны, являются чисто абстрактными формальными утверждениями: доказательство теоремы не может включать эксперименты или другие эмпирические доказательства так же, как эти доказательства используются для поддержки научных теорий.

Гипотеза Коллатца : один из способов проиллюстрировать её сложность — расширить итерацию от натуральных чисел до комплексных чисел. Результатом является фрактал, который (в соответствии с универсальностью) напоминает множество Мандельброта .

Тем не менее, существует определенная степень эмпиризма и сбора данных, связанных с открытием математических теорем. Устанавливая модель, иногда с использованием мощного компьютера, математики могут иметь представление о том, что доказывать, а в некоторых случаях даже о том, как приступить к выполнению доказательства. Например, гипотеза Коллатца была проверена для начальных значений примерно до 2,88 × 10 18 . Гипотеза Римана была проверена для первых 10 триллионов нулей дзета-функции . Ни одно из этих утверждений не считается доказанным.

Такие свидетельства не являются доказательством. Например,  — это некоторое неверное утверждение о натуральных числах, однако явный контпример неизвестен. Известно только, что наименьший контрпример не меньше 10 14 и не больше 104,3 × 1039. Найти явный контрпример с помощью полного перебора невозможно, однако известно, что он существует.

Слово «теория» также существует в математике для обозначения совокупности математических аксиом, определений и теорем, как, например, теория групп. Есть также «теоремы» в науке, особенно в физике, и в технике, но они часто имеют утверждения и доказательства, в которых физические предположения и интуиция играют важную роль; физические аксиомы, на которых основаны такие «теоремы», сами по себе фальсифицируемы.

Примечания

1. Elisha Scott Loomis. . Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Дата обращения 26 сентября 2010.
2. Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров. — Москва: «Советская Энциклопедия», 1988. — С. 580. — 847 с.
3. However, both theorems and scientific law are the result of investigations. See Introduction, The terminology of Archimedes, p. clxxxii: «theorem (θεώρημα) from θεωρεῖν to investigate»
4. Doron Zeilberger. .
5. Петковсек и соавт. 1996.
6. Wentworth, G.; Smith, D.E. Art. 46, 47 // Plane Geometry (неопр.). — Ginn & Co., 1913.
7. Wentworth & Smith Art. 51
8. Следует Wentworth & Smith Art. 79
9. Слово закон также может относиться к аксиоме, правилу вывода или, в теории вероятности, распределению вероятности .
10. Hoffman 1998, p. 204.
11. Hoffman 1998, p. 7.

Раздел 2. Теорема Пифагора

Косинус угла

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Косинус угла а обозначается так: cos а и равен отношению катета АС, прилежащего к этому углу, к гипотенузе АВ, т. е. cos a = АС/АВ.

Теорема 7.1. Косинус угла зависит только от градусной меры угла и не зависит от расположения и размеров треугольника.

Это означает, что у двух прямоугольных треугольников с одним и тем же острым углом косинусы этого угла равны.

Теорема Пифагора

Теорема 7.2. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Из теоремы Пифагора следует, что в прямоугольном треугольнике любой из катетов меньше гипотенузы. Отсюда, в свою очередь, следует, что cos а < 1 для любого острого угла а.

Египетский треугольник

Землемеры Древнего Египта для построения прямого угла пользовались следующим приёмом. Бечёвку узлами делили на 12 равных частей и концы связывали. Затем бечёвку растягивали на земле так, что получался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой (32 + 42= 52).

В связи с указанным способом построения прямого угла треугольник со сторонами 3, 4 и 5 единиц иногда называют египетским.

Перпендикуляр и наклонная

Пусть ВА — перпендикуляр, опущенный из точки В на прямую а, и С — любая точка прямой а, отличная от А. Отрезок ВС называется наклонной, проведённой из точки В к прямой а (рис. 153). Точка С называется основанием наклонной. Отрезок АС называется проекцией наклонной.

Из теоремы Пифагора следует, что если к прямой из одной точки проведены перпендикуляр и наклонные, то любая наклонная больше перпендикуляра, равные наклонные имеют равные проекции, из двух наклонных больше та, у которой проекция больше.

Неравенство треугольника

Если точки А и В различны, то расстоянием между ними называется длина отрезка АВ. Если точки А и В совпадают, то расстояние между ними принимается равным нулю.

Теорема 7.3. Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.

Это значит, что каждое из этих расстояний меньше суммы или равно сумме двух других. Заметим, что в случае, когда точки не лежат на одной прямой, в неравенстве треугольника строгое неравенство. Отсюда следует, что в любом треугольнике каждая сторона меньше суммы двух других сторон.

Соотношения между сторонами и углами в прямоугольном треугольнике

Пусть АВС — прямоугольный треугольник с прямым углом С и острым углом при вершине А, равным а.

• Согласно определению cos а равен отношению катета, прилежащего к углу а, к гипотенузе.
• Синусом угла а (обозначается sin а) называется отношение противолежащего катета ВС к гипотенузе АВ: sin а = ВС/АВ.
• Тангенсом угла а (обозначается tg a) называется отношение противолежащего катета ВС к прилежащему катету АС: tg a = ВС/АС.
• Котангенсом угла а (обозначается ctg a) называется отношение прилежащего катета АС к противолежащему катету ВС: ctga = АС/ВС.

Синус, тангенс и котангенс утла, так же как и косинус, зависят только от величины угла. Из определения sin a, cos a, tg a и ctg a получаем следующие правила:

1. Катет, противолежащий углу а, равен произведению гипотенузы на sin a.
2. Катет, прилежащий к углу а, равен произведению гипотенузы на cos a.
3. Катет, противолежащий углу а, равен произведению второго катета на tg a.
4. Катет, прилежащий к углу а, равен произведению второго катета на ctg a.

Эти правила позволяют, зная одну из сторон прямоугольного треугольника и острый угол, находить две другие стороны; зная две стороны, находить острые углы.

Для sin a, cos a, tg a и ctg a составлены специальные таблицы. Эти таблицы позволяют по данному углу а найти sin a, cos a, tg a и ctg a или по значениям sin a, cos a, tg a и ctg a найти соответствующий угол. В настоящее время для этой цели обычно применяют микрокалькуляторы.

Основные тригонометрические тождества

Эти тождества позволяют, зная одну из величин sin a, cos a, tg a или ctg a, найти три другие.

1. tg a = sin a / cos a.
2. сtg a = cos a / sin a.
3. sin2a + cos2a = 1.
4. 1 + tg2a = 1 / cos2a
5. 1 + ctg2a = 1 / sin2a

Неформальное изложение теорем

С точки зрения логики, многие теоремы имеют форму условного обозначения : если A, то B. Такая теорема утверждает не истинность B, а только то, что B является необходимым следствием A. В этом случае A называется логической гипотезой теоремы, а B — выводом (формально A и B называются предшествующим и последующим утверждениями). Следует подчеркнуть, что логическая гипотеза и математическая гипотеза — суть разные понятия. Так, утверждение «Если n — чётное натуральное число, то n / 2 — натуральное число» — пример теоремы, в которой гипотезой является утверждение «n — чётное натуральное число», а утверждение «n / 2 — также натуральное число» является выводом.

Для доказательства теорема должна быть выражена в виде точного формального утверждения. Тем не менее, для удобства читателя теоремы обычно выражаются не в полностью символической форме, а на естественном языке. Читатель же самостоятельно преобразует неформальное утверждение в формальное.

В математике часто выбирают несколько гипотез и создают теорию, которая состоит из всех утверждений, логически вытекающих из этих гипотез. Гипотезы, которые составляют основу теории, называются аксиомами или постулатами. Область математики, изучающая формальные языки, аксиомы и структуру доказательств, называется теорией доказательств.

Планарная карта с пятью цветами, так что нет двух областей с одинаковым цветом. Это может быть окрашено таким образом только с четырьмя цветами. Теорема о четырёх цветах утверждает, что такие раскраски возможны для любой плоской карты, но каждое известное доказательство включает в себя вычислительный поиск, который слишком длинный, чтобы проверить его вручную.

Некоторые теоремы являются «тривиальными» в том смысле, что они очевидным образом следуют из определений, аксиом и других теорем и не содержат никаких удивительных идей. С другой стороны, некоторые теоремы могут быть названы «глубокими», потому что их доказательства могут быть длинными и трудными, включать области математики, внешне отличные от формулировки самой теоремы, или демонстрировать удивительные связи между различными областями математики. Теорема может быть простой в изложении и в то же время глубокой. Прекрасным примером глубокой теоремы является Великая теорема Ферма. В теории чисел и в комбинаторике, а также в других областях математики имеется множество примеров простых в изложении, но глубоких теорем.

С другой стороны, есть теоремы, имеющие доказательство, которое невозможно записать в простом виде. Наиболее яркими примерами таких теорем являются теорема о четырех цветах и гипотеза Кеплера. Обе эти теоремы известны тем, что они сводятся к определённому алгоритму, который затем проверяется компьютерной программой. Первоначально многие математики не принимали эту форму доказательства, но сейчас она стала разрешённой. Математик Дорон Цейлбергер даже утверждает, что это, пожалуй, единственные нетривиальные результаты, которые когда-либо были доказаны математиками. Многие математические теоремы могут быть сведены к более простым вычислениям, включая полиномиальные тождества, тригонометрические тождества и гипергеометрические тождества.

Интересные факты

Подсчитано, что ежегодно доказывается более четверти миллиона теорем.

Хорошо известный афоризм «математик — это устройство для превращения кофе в теоремы» часто приписывают выдающемуся математику Палу Эрдёшу, который был знаменит доказательством большого количества теорем, числом Эрдёша, характеризующем количество его возможных соавторов и огромным количеством выпиваемого им кофе. Однако это высказывание принадлежит коллеге Эрдёша, Альфреду Реньи (хотя Реньи, произнося эту фразу, скорее всего имел в виду Эрдёша).

Классификация простых конечных групп рассматривается некоторыми математиками как самое длинное доказательство теоремы. Её произвели около 100 авторов в 500 журнальных статьях, занимающих в общей сложности десяток тысяч страниц. Считается, что эти публикации вместе дают полное доказательство, и многие математики надеются сократить и упростить это доказательство. Другая теорема этого типа — проблема четырех красок, чьё компьютерное доказательство слишком длинное, чтобы человек мог его прочитать. Это, безусловно, самое длинное из известных доказательств теоремы, утверждение которых легко понять непрофессионалу.

Связь с научными теориями

Теоремы в математике и теории в науке принципиально различаются по своей эпистемологии . Научная теория не может быть доказана; его ключевым атрибутом является то, что он поддается опровержению , то есть он делает предсказания о мире природы, которые можно проверить экспериментально . Любое несогласие между предсказанием и экспериментом демонстрирует неправильность научной теории или, по крайней мере, ограничивает ее точность или область действия. Математические теоремы, с другой стороны, представляют собой чисто абстрактные формальные утверждения: доказательство теоремы не может включать эксперименты или другие эмпирические доказательства таким же образом, как такие доказательства используются для поддержки научных теорий.

Гипотеза Коллатца : один из способов проиллюстрировать ее сложность — расширить итерацию с натуральных чисел до комплексных. В результате получается фрактал , который (по универсальности ) напоминает множество Мандельброта .

Тем не менее, открытие математических теорем требует некоторой степени эмпиризма и сбора данных. Создавая шаблон, иногда с использованием мощного компьютера, математики могут иметь представление о том, что доказывать, а в некоторых случаях даже план того, как приступить к доказательству. Например, гипотеза Коллатца была проверена для начальных значений примерно до 2,88 × 10 18 . Гипотеза Римана была проверена для первых 10 триллионов нулей дзета-функции . Ни одно из этих утверждений не считается доказанным.

Такие доказательства не являются доказательством. Например, гипотеза Мертенса — это утверждение о натуральных числах, которое теперь известно как ложное, но не существует явного контрпримера (т. Е. Натурального числа n, для которого функция Мертенса M ( n ) равна или превышает квадратный корень из n ). известно: все числа меньше 10 14 обладают свойством Мертенса, а наименьшее число, не обладающее этим свойством, известно только как меньше экспоненты 1,59 × 10 40 , что приблизительно равно 10 в степени 4,3 × 10 39 . Поскольку число частиц во Вселенной обычно считается меньше 10 в степени 100 ( гугол ), нет никакой надежды найти явный контрпример путем исчерпывающего поиска .

Слово «теория» также существует в математике для обозначения совокупности математических аксиом, определений и теорем, как, например, в теории групп (см. Математическую теорию ). Существуют также «теоремы» в науке, особенно в физике, и в инженерии, но они часто содержат утверждения и доказательства, в которых важную роль играют физические предположения и интуиция; физические аксиомы, на которых основаны такие «теоремы», сами по себе опровергаются.

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так: 

Теорема Виета Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента: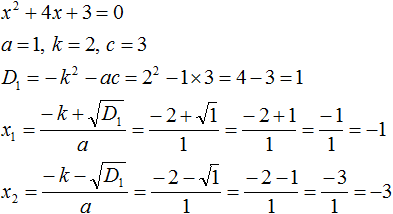

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Доказательство теоремы Виета

Дано квадратное уравнение x2 + bx + c = 0. Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:

Докажем, что следующие равенства верны

• x₁ + x₂ = −b,
• x₁ * x₂ = c.

Формулы корней

Чтобы найти сумму корней x₁ и x₂ подставим вместо них то, что соответствует им из правой части формул корней. Напомним, что в данном квадратном уравнении x2 + bx + c = 0 старший коэффициент равен единице. Значит после подстановки знаменатель будет равен 2.

1. Объединим числитель и знаменатель в правой части.

2. Раскроем скобки и приведем подобные члены:

3. Сократим дробь полученную дробь на 2, остается −b:

Мы доказали: x₁ + x₂ = −b.

Далее произведем аналогичные действия, чтобы доказать о равенстве x₁ * x₂ свободному члену c.

1. Подставим вместо x₁ и x₂ соответствующие части из формул корней квадратного уравнения:

2. Перемножаем числители и знаменатели между собой:

3. Очевидно, в числителе содержится произведение суммы и разности двух выражений. Поэтому воспользуемся тождеством (a + b) * (a − b) = a2 − b2. Получаем:

4. Далее произведем трансформации в числителе:

5. Нам известно, что D = b2 − 4ac. Подставим это выражение вместо D.

6. Далее раскроем скобки и приведем подобные члены:

7. Сократим:

Мы доказали: x₁ * x₂ = c.

Значит сумма корней приведённого квадратного уравнения x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком (x₁ + x₂ = −b), а произведение корней равно свободному члену (x₁ * x₂= c). Теорема доказана.

Как это было

Одним из людей, анализировавших первоначальную рукопись Уайлса с решением теоремы, был Ник Кац. В ходе своего обзора он задал британцу ряд уточняющих вопросов, которые заставили Уайлса признать, что его работа явно содержит пробел. В одной критической части доказательства была допущена ошибка, которая давала оценку для порядка конкретной группы: система Эйлера, используемая для расширения метода Колывагина и Флача, была неполной. Ошибка, однако, не сделала его работу бесполезной — каждая часть работы Уайлса была очень значительной и новаторской сама по себе, как и многие разработки и методы, которые он создал в ходе своей работы и которые затрагивали лишь одну часть рукописи. Тем не менее в этой первоначальной работе, опубликованной в 1993 году, действительно не было доказательства великой теоремы Ферма.

Уайлс провел почти год, пытаясь заново найти решение теоремы — сперва в одиночку, а затем в сотрудничестве со своим бывшим учеником Ричардом Тейлором, но все, казалось, было тщетным. К концу 1993 года распространились слухи, что при проверке доказательство Уайльса потерпело неудачу, но насколько серьезной была эта неудача, известно не было. Математики начали оказывать давление на Уайлса, чтобы он раскрыл детали своей работы, независимо от того, была она выполнена или нет, чтобы более широкое сообщество математиков могло исследовать и использовать все, чего ему удалось добиться. Вместо того, чтобы быстро исправить свою ошибку, Уайлс лишь обнаружил дополнительные сложные аспекты в доказательстве великой теоремы Ферма, и наконец-то осознал, насколько сложной она является.

Уайлс заявляет, что утром 19 сентября 1994 года он был на грани того, чтобы бросить все и сдаться, и почти смирился с тем, что потерпел неудачу. Он готов был опубликовать свою неоконченную работу, чтобы другие могли на ней основываться и найти, в чем он ошибся. Английский математик решил дать себе последний шанс и в последний раз проанализировал теорему, чтобы попытаться понять основные причины, по которым его подход не работал, как вдруг внезапно осознал, что подход Колывагина-Флака не будет работать, пока он не подключит к процессу доказательства еще и теорию Ивасавы, заставив ее работать.

6 октября Уайлс попросил трех коллег (включая Фалтинса) рассмотреть его новую работу, а 24 октября 1994 г. он представил две рукописи — «Модульные эллиптические кривые и последняя теорема Ферма» и «Теоретические свойства кольца некоторых Гекке-алгебр», вторую из которых Уайлс написал совместно с Тейлором и доказал, что были выполнены определенные условия, необходимые для оправдания исправленного шага в основной статье.

Эти две статьи были проверены и, наконец, опубликованы в качестве полнотекстового издания в журнале «Анналы математики» за май 1995 года. Новые расчеты Эндрю были широко проанализированы и научное сообщество в конце концов их признало. В этих работах была установлена теорема модульности для полустабильных эллиптических кривых — последний шаг к доказательству великой теоремы Ферма, спустя 358 лет после того, как она была создана.

Краткая история доказательств

Если n = 4, что доказано самим Ферма, достаточно доказать теорему для индексов n, которые являются простыми числами. В течение следующих двух столетий (1637-1839) гипотеза была доказана только для простых чисел 3, 5 и 7, хотя Софи Жермен обновляла и доказывала подход, который имел отношение ко всему классу простых чисел. В середине 19 века Эрнст Куммер расширил это и доказал теорему для всех правильных простых чисел, в результате чего нерегулярные простые числа анализировались индивидуально. Основываясь на работе Куммера и, используя сложные компьютерные исследования, другие математики смогли расширить решение теоремы, имея цель охватить все основные показатели до четырех миллионов, но док-во для всех экспонентов по-прежнему было недоступным (это означает, что математики обычно считали решение теоремы невозможным, чрезвычайно сложным, или недостижимым с современными знаниями).

Вкладки

После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию

Предостережения

Аксиома Паша отличается от теоремы Паша, которая является утверждением о порядке четырех точек на прямой. Однако в литературе есть много примеров, когда аксиома Паша именуется теоремой Паша. Ярким примером этого является , с. 67).

Аксиому Паша не следует путать с аксиомой Веблена-Юнга для проективной геометрии , которую можно сформулировать следующим образом:

Аксиома Веблена-Юнга для проективной геометрии  —  если линия пересекает две стороны треугольника, то она также пересекает третью сторону.

В утверждении аксиомы Веблена-Юнга не упоминается внутреннее и внешнее пересечения, которое касается только свойства инцидентности пересечения линий. В проективной геометрии концепция промежуточности (необходимая для определения внутреннего и внешнего) недействительна, и все линии пересекаются (поэтому проблема параллельных линий не возникает).

Неприведенное квадратное уравнение

Теорема Виета выполняется только тогда, когда квадратное уравнение является приведённым, то есть его первый коэффициент равен единице:

ax2 + bx + c = 0, где а = 1.

Если квадратное уравнение не является приведенным, но задание связано с применением теоремы, нужно обе части разделить на коэффициент, который располагается перед x2.

1. Получилось следующее приведенное уравнение:

1. Получается коэффициент равен , свободный член — . Значит сумма и произведение корней будут иметь вид:

2. Рассмотрим пример неприведенного уравнения: 4×2 + 5x + 1 = 0. Разделим обе его части на коэффициент перед x2, то есть на 4.

3. Получилось приведённое квадратное уравнение. Второй коэффициент которого равен , а свободный член .
4. Тогда в соответствии с теоремой Виета получаем:

5. Метод подбора помогает найти корни: −1 и 

Записывайте вашего ребенка на бесплатное вводное занятие по математике в Skysmart: порешаем задачки и головоломки на интерактивной платформе и покажем, что математика может быть увлекательным путешествием!