Статистические методы

Статистические методы анализа данных как область научно-практической деятельности

Статистические методы анализа данных применяются практически во всех областях деятельности человека. Их используют всегда, когда необходимо получить и обосновать какие-либо суждения о группе (объектов или субъектов) с некоторой внутренней неоднородностью.

Целесообразно выделить три вида научной и прикладной деятельности в области статистических методов анализа данных (по степени специфичности методов, сопряженной с погруженностью в конкретные проблемы):

а) разработка и исследование методов общего назначения, без учета специфики области применения;

б) разработка и исследование статистических моделей реальных явлений и процессов в соответствии с потребностями той или иной области деятельности;

в) применение статистических методов и моделей для статистического анализа конкретных данных.

Кратко рассмотрим три только что выделенческих методов и моделей, предназначенных для определенной области применения, может быть весьма сложным и математизированным (см., например, монографию ), с другой — результаты представляют не всеобщий интерес, а лишь для некоторой группы специалистов. Можно сказать, что работы вида б) нацелены на решение типовых задач конкретной области применения.

Методы статистического исследования

Между наукой-статистикой и практикой существует тесная взаимосвязь: статистика использует данные практики, обобщает и разрабатывает методы проведения статистических исследований. В свою очередь в практической деятельности применяются теоретические положения статистической науки для решения конкретных управленческих задач. Знание статистики необходимо современному специалисту для принятия решений в условиях стохастики (когда анализируемые явления подвержены влиянию случайностей), для анализа элементов рыночной экономики, в сборе информации, в связи с увеличением числа хозяйственных единиц и их типов, аудите, финансовом менеджменте, прогнозировании.

Для изучения предмета статистики разработаны и применяются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, группировок, обобщающих показателей, динамических рядов, индексный метод и др.). Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации. При этом статистика опирается на такие диалектические категории, как количество и качество, необходимость и случайность, причинность, закономерность, единичное и массовое, индивидуальное и общее. Статистические методы используются комплексно (системно). Это обусловлено сложностью процесса экономико-статистического исследования, состоящего из трех основных стадий: • первая — сбор первичной статистической информации; • вторая — статистическая сводка и обработка первичной информации; • третья — обобщение и интерпретация статистической информации.

Общей методологией изучения статистических совокупностей является использование основных принципов которыми руководствуются в любой науке. К этим принципам, как к своего рода началам относятся следующие:

1. объективность изучаемых явлений и процессов;

2. выявление взаимосвязи и системности в которых проявляется содержание изучаемых факторов;

3. целеполагание, т.е. достижение поставленных целей со стороны исследователя, изучающего соответствующие статистические данные.

Это выражается в получении сведений о тенденциях, закономерностях и возможных последствиях развития изучаемых процессов

Знание закономерностей развития социально-экономических процессов, интересующих общество, имеет важное практическое значение

К числу особенностей статистического анализа данных следует отнести метод массового наблюдения, научной обоснованности качественного содержания группировок и его результатов, вычисление и анализ обобщенных и обобщающих показателей изучаемых объектов.

Что касается конкретных методов экономической, промышленной или статистики культуры, населения, национального богатства и т.п., то здесь могут быть свои специфические методы сбора, группировки и анализа соответствующих совокупностей (суммы фактов).

В экономической статистике, например, широко применяется балансовый метод как наиболее распространенный метод взаимной увязки отдельных показателей в единой системе экономических связей в общественном производстве. К методам применяемым в экономической статистике также относятся составление группировок, исчисление относительных показателей (процентное соотношение), сравнения, исчисление различных видов средних величин, индексов и т.п.

Метод связующих звеньев состоит в том, что два объемных, т.е. количественных показателя сопоставляются на основе существующего между ними отношения. Например, производительность труда в натуральных показателях и отработанного времени, или объем перевозок в тоннах и средней дальности перевозок в км.

Примечания

1. Малая советская энциклопедия. — М.: Советская энциклопедия, 1960. — Т. 8. — С. 1090.
2. Райзберг Б. А., Лозовский Л. Ш., Стародубцева Е. Б. Современный экономический словарь. 5-е изд., перераб. и доп. — М.: ИНФРА-М, 2007. — 495 с. — (Библиотека словарей «ИНФРА-М»)
3. Никитина Е. П., Фрейдлина В. Д., Ярхо А. В. Коллекция определений термина «статистика». — Москва: МГУ, 1972.
4. Чупров А. А. Вопросы статистики. — М.: Госстатиздат ЦСУ СССР, 1960.
5. Никитина Е. П., Фрейдлина В. Д., Ярхо А. Коллекция определений термина «статистика»
6. Гнеденко Б. В. Очерк по истории теории вероятностей. — Москва: УРСС, 2001.
7. Клейн Ф. Лекции о развитии математики в XIX столетии. Часть I. — Москва, Ленинград: Объединенное научно-техническое издательство НКТП СССР, 1937.
8. Плошко Б. Г., Елисеева И. И. История статистики: Учеб. пособие. — Москва, Ленинград: Финансы и статистика, 1990.
9. Huff, Darrell, How to Lie With Statistics, WW Norton & Company, Inc. New York, NY, 1954. ISBN 0-393-31072-8
10. Warne, R. Lazo, M., Ramos, T. and Ritter, N. (2012). Statistical Methods Used in Gifted Education Journals, 2006—2010. Gifted Child Quarterly, 56(3) 134—149. doi: 10.1177/0016986212444122
11. ↑ Encyclopedia of Archaeology (неопр.). — Credo Reference: Oxford: Elsevier Science, 2008.
12. ↑ Cohen, Jerome B. Misuse of Statistics (англ.) // Journal of the American Statistical Association : journal. — JSTOR, 1938. — December (vol. 33, no. 204). — P. 657—674.
13. Freund, J. F. Modern Elementary Statistics (неопр.) // Credo Reference. — 1988.
14. ↑ .
15. Mark Twain. . North American Review. Project Gutenberg (7 сентября 1906). Дата обращения: 23 мая 2007.

1. Предмет, методы и задачи статистики

Статистика как термин может трактоваться в двух значениях:
1) статистика как отрасль знаний (наука);
2) статистика как форма практической деятельности (государственная статистика, ведомственная статистика).

Предмет изучения статистики – это количественная сторона массовых общественных явлений и процессов, неразрывные в связи с их качественным содержанием в конкретных условиях времени и места, изучаемая с целью выявления числовых закономерностей, тенденций. Данное определение считается общепринятым определением, согласно которому статистика стала считаться общественной наукой.
Статистика изучает количественную сторону явлений и процессов в неразрывной связи с их качественной стороной, т. е. измеряя с помощью показателей те или иные явления, показывает, что скрывается за ними, каково их содержание.

Объект изучения статистики – это общество, явления и процессы общественной жизни.
Статистическое исследование совокупностей позволяет устранить случайные факторы и выявить общие черты, закономерности. В подобных случаях статистика опирается на закон больших чисел, который характеризует прямую зависимость полного проявления закономерности от числа наблюдений.
Теоретическую основу статистики составляют такие науки, как философия и экономическая теория. Эти науки исследуют и формируют законы общественного развития, а статистика дает конкретную числовую характеристику закономерностям общественных явлений. В соответствии с философскими законами диалектики статистика изучает явления в их взаимосвязи, развитии (в изменении). Она изучает, как осуществляется переход от количественных изменений к качественным, выясняет, как внедряется новое, прогрессивное в развитии экономики общества.
Если предмет статистики определяет, что конкретно она изучает количественную сторону массовых явлений и процессов, то ее метод характеризует, каким образом это достигается. Базовым, всеобщим является метод познания, или диалектический материализм. Опираясь на этот метод, статистика выработала и свои специфические методы, к которым относятся:
1) метод массового статистического наблюдения, в т. ч. выборочный метод;
2) метод статистической сводки и группировки. При сводке широко используются табличный и графический методы;
3) метод научной обработки и анализа статистических данных с помощью обобщающих показателей.
К таким показателям относятся:
1) абсолютные и относительные величины;
2) средние величины (метод средних);
3) показатели вариации (колеблемости);
4) индексы (индексный метод);
5) методы измерения динамики;
6) показатели тесноты связи.
Помимо вышеназванных, в статистике широко используются и другие методы: балансовый метод, методы математической статистики (дисперсионный анализ, корреляционный и регрессионный анализ) и др.
Основными задачами статистики являются:
1) статистическое наблюдение за развитием экономики и общества с помощью различных видов и способов сбора данных;
2) контроль, проверка содержания различной информации, поступающей в органы статистики;
3) свод отчетности снизу доверху;
4) научная обработка, обобщение, анализ всех материалов наблюдений, в т. ч. выборочных, специально организованных;
5) комплексное изучение экономики, анализ ее состояния, развитие тенденций, закономерностей в масштабах регионов, страны, различных форм собственности, хозяйствования, секторов и отраслей экономики;
6) подготовка и публикация статистических материалов (статистических сборников, ежегодников, пресс-выпусков, докладов) о развитии страны, регионов, отраслей и т. д.;
7) совершенствование учета, отчетности, системы показателей и методов анализа.

методы отбора единиц наблюдения

В зависимости от степени охвата исследования принято различать сплошное и не сплошное статистическое наблюдение. Сплошным называют такое исследование, при котором изучаются все единицы наблюдения объекта исследования.

Не сплошное наблюдение бывает нескольких видов:

монографическое

метод основного массива

выборочное исследование.

Монографическое исследование — глубокое изучение одного человека, одного учреждения, одного села нередко с определенными временными интервалами. Монографическое исследование иногда проводят перед основным с целью разработки программы, изучения различных организационных вопросов.

Метод основного массива — охватывает большую часть единиц изучаемого объекта наблюдения. Этот метод иногда называют несовершенным сплошным. Например, при изучении здоровья детей, родители которых работают на текстильных предприятиях, для анализа отбирают только крупные предприятия.

Выборочный метод.

Механическая выборка — формируется с помощью механического (арифметического) подхода к отбору единиц наблюдения. Например, при необходимости отбора 20% от всей генеральной совокупности можно отобрать каждый 5-й случай.

Случайная выборка — формируется с использованием вероятностных математических методов, например, таблицы случайных чисел.

Типологическая выборка — это выборка, при формировании которой генеральная совокупность разбивается на типы с последующим отбором единиц наблюдения из каждой типической группы. При этом число единиц наблюдения можно отобрать пропорционально численности типической группы (пропорциональный типологический отбор) или непропорционально, т.е. отбирая разное число наблюдений из каждой группы (непропорциональный типологический отбор). Например, исследуемую группу предварительно можно разбить по полу, возрасту, профессии или образованию и отобрать из каждой подгруппы необходимое число единиц наблюдения.

Серийная выборка — формируется с помощью отбора не отдельных единиц наблюдения а целых групп, серий, гнезд, в состав которых входят организованные определенным образом единицы наблюдения. Например, могут быть взяты территориальные образования (деревни, районы), отдельные учреждения (больницы, детские сады и т.п.) Внутри каждой серии изучаются все единицы наблюдения.

Когортный метод — статистическую совокупность составляют относительно однородные группы лиц, объединенных наступлением определенного демографического признака в один и тот интервал времени. Например, при изучении вопросов связанных с рождаемостью, формируют когорту по признаку единого срока рождения — исследование рождаемости по поколениям, или по признаку единого срока вступления в брак — исследование рождаемости по продолжительности семейной жизни.

Метод направленного отбора — позволяет выявить влияние неизвестных факторов при устранении влияния известных. Например, при изучении влияния стажа работающего на травматизм отбираются рабочие одной профессии, одного возраста, одного образовательного уровня.

Метод копи-пара, или способ уравновешивания групп (метод парных сочетаний). В основе его лежит подбор для каждой единицы наблюдения исследуемой группы «копи-пары» по одному или нескольким исследуемым признакам. Например, известно, что на младенческую смертность влияют такие факторы, как масса тела при рождении и пол ребенка. При использовании данного метода для каждого случая смерти ребенка из альтернативной совокупности благополучных исходов подбирают «копи-пару» по массе и полу. Этот способ отбора целесообразно применять для изучения редких явлений.

Прикладная статистика

Прикладная статистика — это наука о том, как обрабатывать данные произвольной природы. Математической основой прикладной статистики и статистических методов анализа является теория вероятностей и математическая статистика.

Описание вида данных и механизма их порождения — начало любого статистического исследования. Для описания данных применяют как детерминированные, так и вероятностные методы. С помощью детерминированных методов можно проанализировать только те данные, которые имеются в распоряжении исследователя. Например, с их помощью получены таблицы, рассчитанные органами официальной государственной статистики на основе представленных предприятиями и организациями статистических отчётов. Перенести полученные результаты на более широкую совокупность, использовать их для предсказания и управления можно лишь на основе вероятностно-статистического моделирования. Поэтому в математическую статистику часто включают лишь методы, опирающиеся на теорию вероятностей.

В простейшей ситуации статистические данные — это значения некоторого признака, свойственного изучаемым объектам. Значения могут быть количественными или представлять собой указание на категорию, к которой можно отнести объект. Во втором случае говорят о качественном признаке.

При измерении по нескольким количественным или качественным признакам в качестве статистических данных об объекте получаем вектор. Его можно рассматривать как новый вид данных. В таком случае выборка состоит из набора векторов. Есть часть координат — числа, а часть — качественные (категоризованные) данные, то говорим о векторе разнотипных данных.

Одним элементом выборки, то есть одним измерением, может быть и функция в целом. Например, описывающая динамику показателя, то есть его изменение во времени, — электрокардиограмма больного или амплитуда биений вала двигателя. Или временной ряд, описывающий динамику показателей определенной фирмы. Тогда выборка состоит из набора функций.

Элементами выборки могут быть и иные математические объекты. Например, бинарные отношения. Так, при опросах экспертов часто используют упорядочения (ранжировки) объектов экспертизы — образцов продукции, инвестиционных проектов, вариантов управленческих решений. В зависимости от регламента экспертного исследования элементами выборки могут быть различные виды бинарных отношений (упорядочения, разбиения, толерантности), множества, нечёткие множества и т. д.

Математическая природа элементов выборки в различных задачах прикладной статистики может быть самой разной. Однако можно выделить два класса статистических данных — числовые и нечисловые. Соответственно прикладная статистика разбивается на две части — числовую статистику и нечисловую статистику.

Числовые статистические данные — это числа, вектора, функции. Их можно складывать, умножать на коэффициенты. Поэтому в числовой статистике большое значение имеют разнообразные суммы. Математический аппарат анализа сумм случайных элементов выборки — это (классические) законы больших чисел и центральные предельные теоремы.

Нечисловые статистические данные — это категоризованные данные, вектора разнотипных признаков, бинарные отношения, множества, нечёткие множества и др. Их нельзя складывать и умножать на коэффициенты. Поэтому не имеет смысла говорить о суммах нечисловых статистических данных. Они являются элементами нечисловых математических пространств (множеств). Математический аппарат анализа нечисловых статистических данных основан на использовании расстояний между элементами (а также мер близости, показателей различия) в таких пространствах. С помощью расстояний определяются эмпирические и теоретические средние, доказываются законы больших чисел, строятся непараметрические оценки плотности распределения вероятностей, решаются задачи диагностики и кластерного анализа, и т. д. (см. ).

В прикладных исследованиях используют статистические данные различных видов. Это связано, в частности, со способами их получения. Например, если испытания некоторых технических устройств продолжаются до определённого момента времени, то получаем так называемые цензурированные данные, состоящие из набора чисел — продолжительности работы ряда устройств до отказа, и информации о том, что остальные устройства продолжали работать в момент окончания испытания. Цензурированные данные часто используются при оценке и контроле надежности технических устройств.

Статистический анализ конкретных данных

Применение статистических методов и моделей для статистического анализа конкретных данных тесно привязано к проблемам соответствующей области. Результаты третьего из выделенных видов научной и прикладной деятельности находятся на стыке дисциплин. Их можно рассматривать как примеры практического применения статистических методов. Но не меньше оснований относить их к соответствующей области деятельности человека.

Например, результаты опроса потребителей растворимого кофе естественно отнести к маркетингу (что и делают, читая лекции по маркетинговым исследованиям). Исследование динамики роста цен с помощью индексов инфляции, рассчитанных по независимо собранной информации, представляет интерес прежде всего с точки зрения экономики и управления народным хозяйством (как на макроуровне, так и на уровне отдельных организаций).

Заказчики прикладных исследований получают отчеты, в которых проблемы соответствующих областей деятельности рассмотрены подробно. Примером такого отчета является монография , посвященная подходам к проблеме вероятностно-статистического моделирования процессов налогообложения.

8.1.1. Меры центральной тенденции

Рассматривая
методы математической статистики,
применяемые для обработки данных
тестовых исследований, можно выделить
группу методов которые могут описывать
те или иные меры центральной тенденции.
Такие меры указывают наиболее типичный
результат, характеризующий выполнение
теста всей группой. Самая известная из
таких мер — среднеарифметическое
значение (М).

Среднеарифметическое
(или выборочное среднее) значение
представляет собой среднюю оценку
изучаемого в эксперименте психологического
качества. Эта оценка характеризует
степень его развития в целом у той группы
испытуемых, которая была подвергнута
исследованию (выборка испытуемых).
Сравнивая среднее значение двух или
нескольких групп, мы можем судить об
относительной степени развития у людей,
составляющих эти группы, оцениваемого
качества

Среднеарифметическое
определяется по следующей формуле:

М
=

где
М — среднеарифметическое значение

n
— количество испытуемых

Пример:
В исследовании объема вербальной
механической памяти, тест «10 слов» в
группе из 12 испытуемых (n = 12), получены
следующие результаты (количество
запомненных слов): 5, 4, 5, 6, 7, 3, 6, 2, 8, 6, 9, 7

Среднеарифметическое
значение (М)

Для
данной выборки среднеарифметическое
значение (М) = 5,6

Другой
мерой центральной тенденции является
мода
(Мо) — наиболее часто встречающийся
результат. В интервальном частотном
распределении мода определяется как
середина интервала, для которого частота
максимальна.

Пример:
В ряду значений 2, 3, 4, 5, 5, 6, 6, 6, 7, 7, 8, 9 модой
является 6, потому, что 6 встречается
чаще любого другого числа.

Обратите
внимание, что мода представляет собой
наиболее часто встречающееся значение
(в данном примере это 6), а не частоту
встречаемости этого значения (в данном
примере равную 3). Когда
два соседних значения имеют одинаковую
частоту и их частота больше частот любых
других значений, мода вычисляется как
среднее арифметическое этих двух
значений

Когда
два соседних значения имеют одинаковую
частоту и их частота больше частот любых
других значений, мода вычисляется как
среднее арифметическое этих двух
значений.

Пример:
в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом
расположенных значений 2 и 5 совпадают
и равняются 3. Эта частота больше, чем
частота других значений 1 и 6 (у которых
она равна 1). Следовательно, модой этого
ряда будет величина

Третья
мера центральной тенденции — медиана
(Ме), — результат, находящийся в середине
последовательности показателей, если
их расположить в порядке возрастания
или убывания. Справа и слева от медианы
(Ме) в упорядоченном ряду остается по
одинаковому количеству данных (50% и
50%). Если ряд включает в себя четное
количество признаков, то медианой (Ме)
будет среднее, взятое как полусумма
двух центральных значений ряда.

Пример:
Найдем медиану выборки: 5, 4, 5, 6, 7, 3, 6, 2,
8, 6, 9, 7.

Упорядочим
выборку: 2, 3, 4, 5, 5, 6, / 6, 6, 7, 7, 8, 9. Поскольку
здесь имеется четное число элементов,
то существует две «середины» — 6 и 6. В
этом случае медиана определяется как
среднее арифметическое этих значений.

Ме

Пример:
Найдем медиану выборки с нечетным
количеством значений: 9, 3, 5, 8, 4, 11, 13.

Сначала
упорядочим выборку по величинам входящих
в нее значений. Получим: 3, 4, 5, 8, 9, 11, 13.
Поскольку в выборке семь элементов,
четвертый по порядку элемент будет
серединой ряда. Таким образом, медианой
будет четвертый элемент — 8

Значения
Ме и Мо полезны для того, чтобы установить
является ли распределение частных
значений изучаемого признака симметричным
и приближающимся к нормальному
распределению. Среднее арифметическое
(М), медиана (Ме) и мода (Мо) для нормального
распределения обычно совпадают или
очень мало отличаются друг от друга.
При нормальном распределении результатов
график распределения имеет форму
колокола (рис. 2).

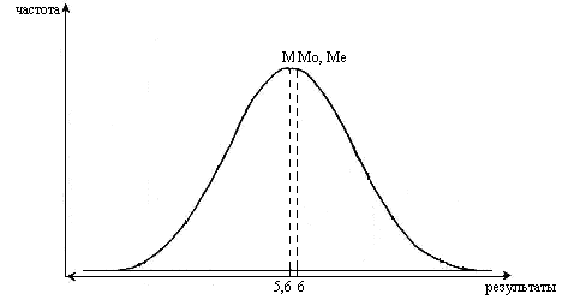
Рис. 2. График
нормального распределения результатов
исследования

Крылатая фраза

Основная статья: Ложь, наглая ложь и статистика

Наиболее известная (и одна из лучших) критика прикладной статистики, «Существуют три вида обмана: ложь, наглая ложь и статистика», англ. There are three kinds of lies: lies, damned lies, and statistics) традиционно приписывается премьер-министру Великобритании Бенджамину Дизраэли, после атрибуции Марка Твена в публикации «Главы моей автобиографии» (журнал North American Review 5 июля 1907 года): «Цифры обманчивы, — писал он, — я убедился в этом на собственном опыте; по этому поводу справедливо высказался Дизраэли: „Существует три вида лжи: ложь, наглая ложь и статистика“». Однако этой фразы нет в работах Дизраэли, её происхождение спорно. В 1964 году К. Уайт (англ. Colin White) предположил авторство Франсуа Мажанди (1783—1855), который сказал фразу по-французски: фр. Ainsi l’altération de la vérité qui se manifeste déjà sous la forme progressive du mensonge et du parjure, nous offre-t-elle au superlatif, la statistique («Модификация правды, которая проявляется в сравнительной степени неправды и лжесвидетельства, имеет и суперлатив, статистику»). По словам Уайта, «мир нуждался в этой фразе, и несколько человек могли бы гордиться, придумав её».

Источники информации

Сбор данных может осуществляться по-разному. Главное, чтобы способы не нарушали закон и не ущемляли интересы других лиц. Если говорить о СМИ, то для них ключевыми источниками информации выступают государственные статистические органы. Эти структуры должны:

1. Собирать отчетные сведения в соответствии с утвержденными программами.
2. Группировать информацию по тем или иным критериям, наиболее значимым для исследуемого явления, формировать сводки.
3. Проводить собственный статистический анализ.

В задачи уполномоченных госорганов входит также предоставление полученных ими данных в отчетах, тематических подборках или пресс-релизах. В последнее время статистика публикуется на официальных сайтах госструктур.

Кроме указанных органов, информацию можно получить в Едином госреестре предприятий, учреждений, объединений и организаций. Цель его создания состоит в формировании единой информационной базы.

Для проведения анализа можно использовать информацию, полученную от межправительственных организаций. Существуют специальные базы данных экономической статистики стран.

Часто информация поступает от частных лиц, общественных организаций. Эти субъекты обычно ведут свою статистику. Так, к примеру, Союз охраны птиц в России регулярно устраивает так называемые соловьиные вечера. В конце мая через СМИ организация приглашает всех желающих поучаствовать в подсчете соловьев на территории Москвы. Полученные сведения обрабатываются группой экспертов. После этого сведения переносятся в специальную карту.

Многие журналисты обращаются за информацией к представителям других авторитетных СМИ, пользующихся у аудитории популярностью. Распространенным способом получения данных является опрос. При этом опрашиваемыми могут стать как рядовые граждане, так и эксперты в какой-либо области.