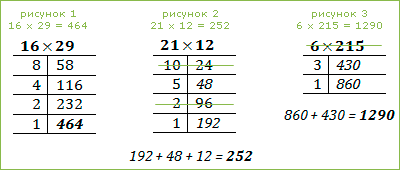Решаем задачу нахождения длины наибольшей возрастающей подпоследовательности

Решение за O( n ^ 2)

Рассмотрим следующую возрастающую подпоследовательность:

5, 6, 12

теперь взглянем на следующее число после последнего элемента в последовательности — это 3.

Может ли оно быть продолжением нашей последовательности? Нет. Оно меньше чем 12.

А 24 ?

Оно да, оно может.

Соответственно длина нашей последовательности равна теперь 3 + 1, а последовательность выглядит так:

5, 6, 12, 24

Вот где переиспользование предыдущих вычислений: мы знаем что у нас есть подпоследовательность 5, 6, 12, которая имеет длину 3 и теперь нам легко добавить к ней 24. Теперь у вас есть ощущение того, что мы можем это использовать, только как?

Давайте заведем еще один дополнительный массив (вот он наш cache, вот оно наше ДП), в котором будем хранить размер возрастающей подпоследовательности для n-го элемента.

Выглядеть это будет так:

Наша задача — заполнить массив counts правильными значениями. Изначально он заполнен единицами, так как каждый элемент сам по себе является минимальной возрастающей подпоследовательностью.

“Что за загадочные i и j?” — спросите вы. Это индексы итераторов по массиву, которые мы будем использовать. Изменяться они будут с помощью двух циклов, один в другом. i всегда будет меньше чем j.

Сейчас j смотрит на 10 — это наш кандидат в члены последовательностей, которые идут до него. Посмотрим туда, где i, там стоит 5.

10 больше 5 и 1 <= 1, counts <= counts? Да, значит counts = counts + 1, помните наши рассуждения в начале?

Теперь таблица выглядит так.

Смещаем j.

Результат:

Имея перед глазами эту таблицу и понимая какие шаги нужно делать, мы теперь легко можем реализовать это в коде.

→ Реализация на Objective-C
→ Тесты

Вы не могли не заметить два вложенных цикла в коде, а там где есть два вложенных цикла проходящих по одному массиву, есть и квадратичная сложность O(n^2), что обычно не есть хорошо.

Теперь, если вы билингвал, вы несомненно зададитесь вопросом “Can we do better?”, обычные же смертные спросят “Могу ли я придумать алгоритм, который сделает это за меньшее время?”

Ответ: “да, можете!”

Чтобы сделать это нам нужно вспомнить, что такое бинарный поиск.

Свойства сходящихся последовательностей

Сходящиеся последовательности обладают рядом свойств.

Свойство 1. Если последовательность сходится, то только к одному пределу.

Свойство 2. Если последовательность сходится, то она ограничена.

Свойство 3. Если последовательность монотонна и ограничена, то она сходится (теорема Вейерштрасса).

Предел стационарной последовательности равен значению любого члена последовательности:.

Теорема. Если , то

1. Предел суммы равен сумме пределов:

2. Предел произведения равен произведению пределов:

3. Предел частного равен частному пределов:

(при c≠0).

4. Постоянный множитель можно вывести за знак предела:

Пример 7. Найти предел последовательности:

Решение. Так как , то

Пример 8. Найти предел последовательности:

Решение. Применив правило «предел суммы» теоремы, получим

Пример 9. Вычислить:

Решение. Делим числитель и знаменатель дроби на наивысшую из имеющихся степень переменного n. Далее используем правило «предел суммы» для числителя и знаменателя и правило «предел частного»:

Определение

Есть несколько эквивалентных способов определения последовательности Туэ – Морса.

Прямое определение

При двоичном счете сумма цифр по модулю 2 представляет собой последовательность Туэ-Морса.

Чтобы вычислить n- й элемент t _n , запишите число n в двоичном формате . Если количество единиц в этом двоичном разложении нечетное, то t _n  = 1, если четное, то t _n  = 0. По этой причине John H. Conway et al . называть номера n, удовлетворяющие t _n  = 1 одиозным (для нечетных ) номеров и номерам, для которых t _n  = 0, злым (для четных ) номеров. Другими словами, t _n  = 0, если n — злое число, и t _n  = 1, если n — одиозное число .

Генерация быстрой последовательности

Этот метод приводит к быстрому способу вычисления последовательности Туэ – Морса: начать с t  = 0 , а затем для каждого n найти бит наивысшего порядка в двоичном представлении n, который отличается от того же бита в представление n  — 1 . (Этот бит можно изолировать, позволив x быть побитовым исключающим ИЛИ для n и n  — 1 , сдвинув x вправо на один бит и вычислив исключающее ИЛИ этого сдвинутого значения с помощью x .) Если этот бит имеет четный индекс, t _n отличается от t _{n  — 1} , а в остальном то же самое, что t _{n  — 1} .

В форме псевдокода:

generateSequence(seqLength):
    value = 
    for n =  to seqLength-1 by 1     
        x = n ^ (n-1)                         
        if ((x ^ (x>>1)) & x55555555):
            value = 1 - value
        return value

Результирующий алгоритм требует постоянного времени для генерации каждого элемента последовательности, используя только логарифмическое количество битов (постоянное количество слов) памяти.

Отношение рецидива

Последовательность Туэ – Морса — это последовательность t _n, удовлетворяющая рекуррентному соотношению

тзнак равно,т2пзнак равнотп,т2п+1знак равно1-тп,{\ displaystyle {\ begin {align} t_ {0} & = 0, \\ t_ {2n} & = t_ {n}, \\ t_ {2n + 1} & = 1-t_ {n}, \ end { выровнено}}}

для всех неотрицательных целых чисел n .

L-система

Последовательность Туэ – Морса, порожденная L-системой

Последовательность Туэ – Морса является морфическим словом : это результат следующей системы Линденмайера :

Переменные	0, 1
Константы	Никто
Начало
Правила	(0 → 01), (1 → 10)

Характеризация с использованием побитового отрицания

Последовательность Туэ – Морса в приведенной выше форме как последовательность битов может быть определена рекурсивно с использованием операции побитового отрицания . Итак, первый элемент равен 0. Затем, как только первые 2 n элементов были указаны, образуя строку s , следующие 2 n элементов должны образовать побитовое отрицание s . Теперь мы определили первые 2 n +1 элементов и приступаем к рекурсии.

Подробное изложение первых нескольких шагов:

• Начнем с 0.
• Побитовое отрицание 0 равно 1.
• Объединяя их, первые 2 элемента — 01.
• Поразрядное отрицание 01 равно 10.
• Объединяя их, получаем первые 4 элемента 0110.
• Поразрядное отрицание 0110 равно 1001.
• Объединяя их, получаем первые 8 элементов 01101001.
• И так далее.

Так

• Т = 0.
• Т ₁ = 01.
• Т ₂ = 0110.
• Т ₃ = 01101001.
• Т ₄ = 0110100110010110.
• Т ₅ = 01101001100101101001011001101001.
• Т ₆ = 0110100110010110100101100110100110010110011010010110100110010110.
• И так далее.

Бесконечный продукт

Последовательность также может быть определена:

∏язнак равно∞(1-Икс2я)знак равно∑jзнак равно∞(-1)тjИксj,{\ displaystyle \ prod _ {i = 0} ^ {\ infty} \ left (1-x ^ {2 ^ {i}} \ right) = \ sum _ {j = 0} ^ {\ infty} (- 1 ) ^ {t_ {j}} x ^ {j},}

где t _j — j- й элемент, если мы начнем с j = 0.

2 вариант

1. Верно ли утверждение, что решение любой задачи можно описать как последовательность действий (шагов)?

1) да
2) нет

2. Большую (трудную) задачу и простую задачу разбили на одинаково мелкие шаги. Для решения какой задачи количество действий (шагов) больше?

1) для большой задачи
2) для простой задачи
3) одинаково

3. Что такое алгоритм?

1) последовательность действий или шагов
2) описание конечной последовательности шагов в решении задачи, приводящей от исходных данных к требуемому результату
3) оба утверждения верны
4) ни одно утверждение не верно

4. Дан прямоугольник со сторонами а и b. Известно, что a = 10 см; b на 2 см меньше. Требуется найти Р — периметр прямоугольника. Выберите верный алгоритм решения задачи.

1) вычислить b = а − 2 (10 − 2 = 8);
вычислить Р = 2 х (а + b) (2 х (10 + 8) = 36);
2) вычислить Р = а + а − 2 + а + а − 2 (10 + 10 − 2 + 10 + 10 − 2 = 36)
3) вычислить b = а − 2 (10 − 2 = 8);
вычислить с = а х 2 (10 х 2 = 20);
вычислить d = b х 2 (8 х 2 = 16);
вычислить Р = с + d (20 + 16 = 36);
4) все алгоритмы верны

5. Какое действие не входит в алгоритм «пойти за продуктами в магазин»?

1) написать список продуктов
2) убрать комнату
3) пойти в магазин
4) купить продукты по списку

6. Может ли изменение порядка действий в алгоритме привести к неверному результату?

1) да
2) нет

7. Кто исполняет алгоритмы?

1) человек
2) робот или компьютер
3) оба утверждения верны
4) ни одно утверждение не верно

Ответы на тест по информатике Жизненные задачи. Последовательность действий. Алгоритм для 6 класса1 вариант
1-1
2-2
3-3
4-3
5-2
6-1
7-22 вариант
1-1
2-1
3-2
4-4
5-2
6-1
7-3

Решение за O (n * log n)

Теперь мы будем проходить по нашему исходному массиву при этом заполняя новый массив, в котором будет храниться возрастающая подпоследовательность. Еще один плюс этого алгоритма: он находит не только длину максимальной возрастающей подпоследовательности, но и саму подпоследовательность.

Как же двоичный поиск поможет нам в заполнении массива подпоследовательности?

С помощью этого алгоритма мы будем искать место для нового элемента в вспомогательном массиве, в котором мы храним для каждой длины подпоследовательности минимальный элемент, на котором она может заканчиваться.

Если элемент больше максимального элемента в массиве, добавляем элемент в конец. Это просто.

Если такой элемент уже существует в массиве, ничего особо не меняется. Это тоже просто.

Что нам нужно рассмотреть, так это случай когда следующий элемент меньше максимального в этом массиве. Понятно, что мы не можем его поставить в конец, и он не обязательно вообще должен являться членом именно максимальной последовательности, или наоборот, та подпоследовательность, которую мы имеем сейчас и в которую не входит этот новый элемент, может быть не максимальной.

Все это запутанно, сейчас будет проще, сведем к рассмотрению 2-х оставшихся случаев.

1. Рассматриваемый элемент последовательности (x) меньше чем наибольший элемент в массиве (Nmax), но больше чем предпоследний.
2. Рассматриваемый элемент меньше какого-то элемента в середине массива.

В случае 1 мы просто можем откинуть Nmax в массиве и поставим на его место x. Так как понятно, что если бы последующие элементы были бы больше чем Nmax, то они будут и больше чем x — соответственно мы не потеряем ни одного элемента.

Случай 2: для того чтобы этот случай был нам полезен, мы заведем еще один массив, в котором будем хранить размер подпоследовательности, в которой этот элемент является максимальным. Собственно этим размером и будет являться та позиция в первом вспомогательном массиве для этого элемента, которую мы найдем с помощью двоичного поиска. Когда мы найдем нужную позицию, мы проверим элемент справа от него и заменим на текущий, если текущий меньше (тут действует та же логика как и в первом случае)

Не расстраивайтесь, если не все стало понятно из этого текстового объяснения, сейчас я покажу все наглядно.

Нам нужны:

1. Исходная последовательность
2. Создаем мутабельный массив, где будем хранить возрастающие элементы для подпоследовательности
3. Создаем мутабельный массив размеров подпоследовательности, в которой рассматриваемый элемент является максимальным.

Результат:

→ Реализация на Objective-C
→ Тесты

Бинарный поиск O(log n)

Бинарный поиск работает только на отсортированных массивах. Например, нам нужно найти позицию числа n в отсортированном массиве:
1, 5, 6, 8, 14, 15, 17, 20, 22

Зная что массив отсортирован, мы всегда можем сказать правее или левее определенного числа в массиве искомое число должно находиться.

Мы ищем позицию числа 8 в этом массиве. С какой стороны от середины массива оно будет находиться? 14 — это число в середине массива. 8 < 14 — следовательно 8 левее 14. Теперь нас больше не интересует правая часть массива, и мы можем ее отбросить и повторять ту же самую операцию вновь и вновь пока не наткнемся на 8. Как видите, нам даже не нужно проходить по всем элементам массива, сложность этого алгоритма < O( n ) и равна O (log n).

Для реализации алгоритма нам понадобятся 3 переменные для индексов: left, middle, right.

Ищем позицию числа 8.

Мы отгадали где находится 8 с трёх нот.

История

Последовательность Туэ – Морса была впервые изучена Эженом Пруэ в 1851 году, который применил ее к теории чисел . Однако Пруэ не упомянул последовательность явно; это было оставлено Акселю Туэ в 1906 году, который использовал его для изучения комбинаторики слов . Последовательность была доведена до всеобщего внимания только в работе Марстона Морса в 1921 году, когда он применил ее к дифференциальной геометрии . Последовательность была открыта независимо много раз, не всегда профессиональными математиками-исследователями; Например, Макс Эйве , шахматный гроссмейстер , обладавший титулом чемпиона мира с 1935 по 1937 год, и учитель математики , открыл его в 1929 году в приложении к шахматам : используя его свойство отсутствия кубов (см. выше), он показал, как обойти правило, направленное на предотвращение бесконечно затяжных игр, объявив повтор ходов ничьей.

Предел числовой последовательности

Точка, к которой приближаются члены последовательности при увеличении n, называется пределом последовательности. Для последовательности (10) пределом является число 0. Более строго предел последовательности определяется так:

Определение 8. Число k называют пределом последовательности (y_n), если для любой заранее выбранной окресности точки k, можно выбрать такой номер n, чтобы все члены последовательности, начиная с номера n содержались в указанной окрестности.

Если k является пределом последовательности (y_n), то пишут ( стремится к k или сходится к k).

Обозначают это так:

Выраженние (11) читается так: предел проследовательности , при стремлении n к бесконечности равен k.

Изложим некоторые пояснения к определению 8.

Пусть выполнено (11). Возьмем окрестность точки k, т.е. интервал , где радиус этой окрестности ( >0). По определению, существует номер n, начиная с которого вся последовательность содержится в указанной окресности, т.е.

Если же взять другую окресность (пусть ), то найдется другой номер n₁, начиная с которого, вся последовательность содержится в указанной окрестности, но этот номер будет больше n₁ > n.

Пример 4. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 0. Пусть ее радиус равен r. Тогда всегда можно выбирать n так, чтобы .

Пусть, например, r=0.001. Вычислим n‘ из уравнения

Имеем:

В качестве n берем 501. Имеем:

или

Запишем члены последовательности (12) начиная с номера 501:

Далее, учитывая (13), имеем:

Следовательно, все члены последовательности (12) начиная с номера 501 попадают в окресность . А по определению 8, это означает:

Пример 5. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 2. Пусть ее радиус равен r. Тогда всегда можно выбирать n так, чтобы

Рашим (15) относительно n:

Получили

Неравенство в (17) всегда выполняется так как n натуральное число, а правая часть неравенства отрицательно (это означает, что для любого n). Из неравенства (16) можно найти номер n, начиная с которого члены последовательности попадают в окресность (2−r; 2+r). Например, пусть r=0.001, тогда . Тогда нужно брать n=2000. И тогда все члены последовательности, начиная с номера 2000 попадают в окрестность (2−r; 2+r).

Запишем члены последовательности, начиная с номера 2000:

Легко проверить, что . Тогда, учитывая, что данная последовательность возрастающая (см. пример 1), получим:

Пример 6. Найти предел последовательности

Решение. Выполним некоторые преобразования выражения (18):

Тогда последовательность (18) можно переписать так:

Как видно из (19), пройдя по членам последовательности слева направо, из числа 1 вычитается все меньшее и меньшее положительное число. Т.е. последовательность приближается к числу 1. Тогда 1 является пределом последовательности (19) и (18):

На Рис. 3 представлена функция . Абсцисы нарисованных точек это номера членов последовательности, а ординаты образуют последовательность (18) (или (19)). Прямая y=1 (горизонтальная пунктирная линия) называется горизонтальной асимптотой. Как видно из Рис.3 последовательность приближается к горизонтальной асимптоте.

Числовые

Числовые последовательности — это один из основных объектов, рассмотрением которого занимается раздел математики под названием математический анализ. Его начинают изучать в старших классах средней школы и продолжают более подробно в институтах.

Числовых последовательностей бесчисленное число Но с точки зрения создания головоломок и занимательных задач нам интересно работать с простыми, известными и интересными последовательностями. Задачка может при этом выглядеть очень просто: «Продолжи последовательность чисел…»

• Натуральные числа — 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, … (ими можно посчитать, например, яблоки)
• Чётные числа — 2,4,6,8,10,12,14,16,18,20,22,24,26,28,30, … (делятся без остатка на 2)
• Нечётные числа — 1,3,5,7,9,11,13,15,17,19,21,23,25,27,29, … (не делятся без остатка на 2)
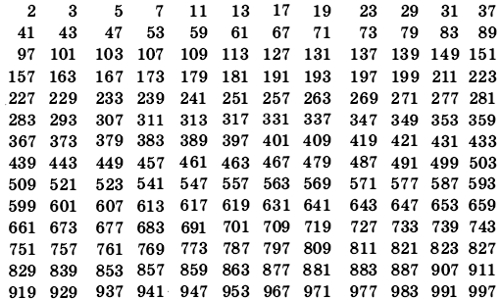
• Простые числа — 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, … (делятся только на себя и на 1)

Числа Фибоначчи — 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … (каждое последующее число равно сумме двух предыдущих чисел)

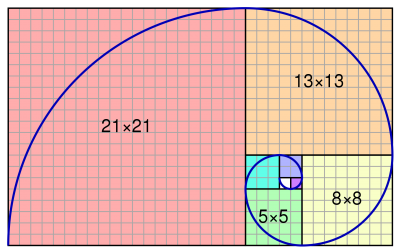
Ряды Фарея — возрастающий ряд всех положительных несократимых правильных дробей, знаменатель которых меньше или равен n

`F_1={0/1,1/1}; `
`F_2={0/1,1/2,1/1}; `
`F_3={0/1,1/3,1/2,2/3,1/1}; `
`F_4={0/1,1/4,1/3,1/2,2/3,3/4,1/1}; `
`F_5={0/1,1/5,1/4,1/3,2/5,1/2,3/5,2/3,3/4,4/5,1/1}; `
`F_6={0/1,1/6,1/5,1/4,1/3,2/5,1/2,3/5,2/3,3/4,4/5,5/6,1/1}; `
`F_7={0/1,1/7,1/6,1/5,1/4,2/7,1/3,2/5,3/7,1/2,4/7,3/5,2/3,5/7,3/4,4/5,5/6,6/7,1/1}; `
`F_8={0/1,1/8,1/7,1/6,1/5,1/4,2/7,1/3,3/8,2/5,3/7,1/2,4/7,3/5,5/8,2/3,5/7,3/4,4/5,5/6,6/7,7/8,1/1}; `

Фигурные числа — если из камушков выкладывать разные фигуры – треугольники, квадраты, пятиугольники и т.п. – всё большего размера, то получатся последовательности фигурных чисел, соответственно, треугольных, квадратных, пятиугольных и т.д.

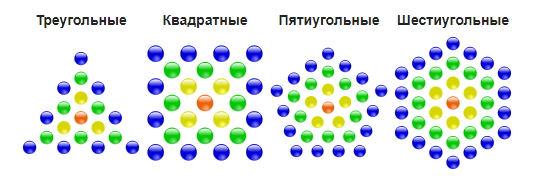
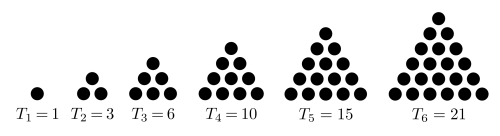
Причём фигурные числа могут быть как плоские, так и объёмные. Например, вот так как получаются квадратные пирамидальные числа.

А вот так образуются тетраэдральные числа.

Также последовательности чисел можно получить, подсчитывая число вершин, рёбер и граней в различных объёмных фигурах типа платоновых тел, архимедовых тел, многогранников Джонсона и т.п.

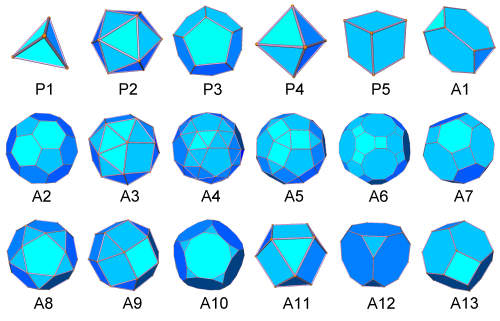
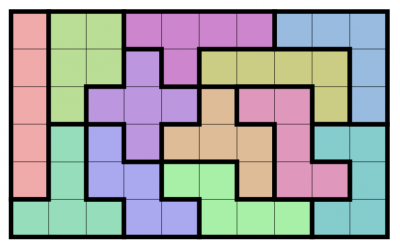
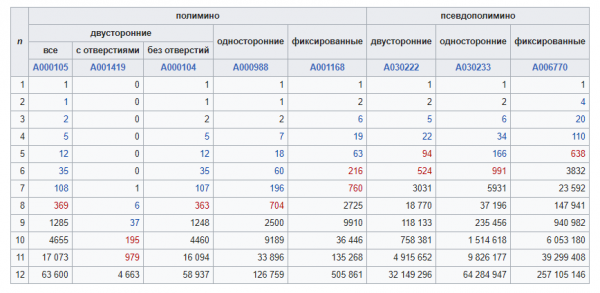
А ещё можно подсчитывать число всевозможных полимино.

Нематематические

Бывают такие числовые последовательности, которые не очень относятся к математике. Например, порядок чисел на барабане в казино или на дартсе.

Системы счисления

В разных странах в разные времена применялись различные, в том числе непозиционные системы счисления. Если сейчас записать этими числами даже обычный ряд натуральных чисел, то получится настоящая головоломка.

Последовательность Фибоначчи O(n)

Последовательность Фибоначчи популярна и окружена легендами, разглядеть ее пытаются (и надо признать, им это удается) везде, где только можно. Принцип же ее прост. n-ый элемент последовательности равен сумме n-1 и n-2 элемента. Начинается соответственно с 0 и 1.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …

Берем 0, прибавляем 1 — получаем 1.
Берем 1, прибавляем 1 — получаем 2.
Берем 1, прибавляем 2 — получаем, ну вы поняли, 3.

Собственно нахождение n-го элемента этой последовательности и будет нашей задачей. Решение кроется в самом определении этой последовательности. Мы заведем один мутабельный массив, в который будем сохранять промежуточные результаты вычисления чисел Фибоначчи, т.е. те самые n-1 и n-2.

Псевдокод:

→ Пример решения на Objective-C
→ Тесты

Вот и всё, в этом массиве numbers вся соль ДП, это своего рода кэш (Caсhe), в который мы складываем предыдущие результаты вычисления этой же задачи, только на меньшей размерности (n-1 и n-2), что дает нам возможность за одно действие найти решение для размерности n.

Этот алгоритм работает за O(n), но использует немного дополнительной памяти — наш массив.

Вернемся к нахождению длины максимальной возрастающей подпоследовательности.

Задача от лектора

На тренинге по искусству презентации лектор рассказывает о необходимости думать нешаблонно и чертит на доске три картинки:

Выходит прекрасная девушка-менеджер и рисует фигуру:

«Тааак…»- говорит лектор,-«все правильно, а теперь объясните — почему?» Девушка объясняет:»Это дорожные знаки: первый — стрелка с направлением движения, второй — перевернутая рюмка, третий — перевернутая чашка с идущим от нее паром, наверное следующий знак будет вилка». Лектор впадает в недоумение:»Первый раз за шесть лет преподавания вижу, что абсолютно неправильные выводы приводят к совершенно правильному результату…». Так что на самом деле нарисовал лектор? 

• Забавные головоломки
• Последовательности

Возрастающие и убывающие последовательности

Определение 3. Последовательность, в которой каждый последующий член (кроме первого) больше предыдующего, называется возрастающей:

Определение 4. Последовательность, в которой каждый последующий член (кроме первого) меньше предыдующего, называется убывающей:

Возрастающие и убывающие последовательности называются также монотонными последовательностями.

Пример 1. Выяснить, монотонна ли последовательность

Решение. Запишем n+1 член последовательности (подставим вместо n, n+1):

Найдем разность членов и :

или

Так как n=1,2,3,… то правая часть уравнения (3) положительна. Тогда:

или

Таким образом, каждый последующий член последовательности больше предыдующего. Следовательно последовательность является возрастающим (и монотонным).

Пример 2. Выяснить, при каких значениях a последовательность (b_n) является возрастающей и при каких, убывающей:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

или

Посмотрим на правую часть выражения (4). Если a<10, то . Тогда последовательность является возрастающей. Если a>10, то . Тогда последовательность является убывающей. При a=10 . Последовательность имеет одинаковые члены:

т.е. имеем дело с последовательностью

Очевидно, что последовательность (5) не является монотонной. Она является стационарной последовательностью.

Навигация

• ФОРУМ
• Забавные головоломки
• Задачи с подвохом
• Старинные и сказочные головоломки
• Математические задачи
  • Алгоритмы
  • Вероятности
  • Вычисления
  • Геометрия
  • Комбинаторика
  • Логика и рассуждения
  • Принцип Дирихле
  • Соответствия
  • Числовые ребусы
• Задачи из книги Р. Смаллиана
• Загадки про время
• Задачи со словами
  • Анаграммы
  • Антифразы
  • Логогрифы
  • Метаграммы
  • Омографы
  • Омонимы
  • Псевдонаучный бред
  • Шарады
• Несерьезные задачи
• Физические задачи
• Детские загадки
  • Природные явления
  • Животные
  • Растения
  • Инструменты и предметы
  • Прочие
• Взвешивания и переливания
• Головоломки со спичками
• Последовательности
• Задачи для нестандартно мыслящих
• Логические трюки
• Исторические задачи
• Фокусы
• Задачи по картинкам
• Головоломки общества МЕНСА
• WWW-задачи
• Дитлоиды
• Скачать книги с головоломками
• Друзья сайта
• Флеш-игры

Итоги

Мы с вами сейчас рассмотрели 4 алгоритма разной сложности. Это сложности, с которыми вам приходится встречаться постоянно при анализе алгоритмов:

О( log n ), О( n ), О( n * log n ), О( n ^ 2 )

Эта картинка из вот этой статьи

Еще мы рассмотрели примеры использования Динамического Программирования, тем самым расширив наш инструмент разработки и понимания алгоритмов. Эти принципы пригодятся вам при изучении других проблем.

Для лучшего понимания я рекомендую вам закодировать эти проблемы самим на привычном вам языке. А еще было бы здорово, если бы вы запостили ссылку на ваше решение в комментах.

Еще предлагаю подумать над тем как доработать последний алгоритм за O (n * log n ) так чтобы вывести еще и саму наибольшую подпоследовательность. Ответ напишите в комментах.

Всем спасибо за внимание, до новых встреч!

Ссылки:Вопрос на Stackoverflow.comПримеры реализации на C++ и JavaВидео с объяснением