Числа фибоначчи: нескучные математические факты

Вклад Фибоначчи в арифметику — Книга абака (Liber abaci)

В Европе математика пришла в упадок после падения греческой культуры. Сначала индейцы положили начало новому расцвету с развитием платежных систем и арифметики, а затем арабы, которые продвинулись в развитии с установлением плоскостной и пространственной тригонометрии. Ситуация была такова, что знания необходимо было распространять в Европе, и никто не был лучше подготовлен для этого, чем Фибоначчи, который освоил и расширил все эти познания.

В 1202 году была опубликована его работа «Liber abaci» (Книга абака), состоящая из 15 разделов, первое европейское общее представление арифметики. Леонардо Пизанский в своём труде вводит индо-арабские цифры, тут же описывает алгоритм умножения (который в новой системе во много раз проще, чем в старой, римской) и показывает, как преобразовать числа из старой системы в новую. Это была трудная задача, потому что было широко распространено недоверие к этим цифрам. В 1299 году городские отцы во Флоренции запретили их использование.

Книга абака (Liber abaci)

О Фибоначчи рассказывается следующая история: В 1225 году в Пизе был конкурс по расчетам. Участникам пришлось решать сложные задачи. Одной из таких задач было:

Найти (рациональное) квадратное число, которое, будучи увеличено или уменьшено на 5, вновь даёт (рациональные) квадратные числа.

Фибоначчи нашел решение и вышел из конкурса победителем. Леонардо попросил присутствовавшего на конкурсе императора Фридриха II содействовать распространению арабских цифр. Фридрих II обещал, но даже он не смог это исполнить. Понадобилось время до 1494 года, чтобы Медичи полностью перешли на арабские цифры. Тем не менее, книга Фибоначчи внесла свой вклад в их распространение и переход к десятичной системе счисления.

В принципе, «Liber abaci» резюмировала, систематизировала и обогатила все математические знания того времени, и эта работа не была превзойдена на протяжении длительного времени. В ней можно найти правила деления на 2, 3, 5 и 9, методы определения наименьшего общего кратного, для которого ранее просто использовалось произведение чисел. Кроме того, представлены методы решения задач с пропорциями, решения задач со смещением, показаны способы решения систем уравнений (до семи неизвестных), продемонстрированы решения уравнений более высокой степени. Наконец, описаны методы аппроксимации для кубических корней, в которых происходит итерация.

В 1220 году последовала вторая работа Фибоначчи «Практика геометрии» — это термин, используемый средневековыми землемерами, известными в наше время как геодезисты. Фибоначчи написал для этих ремесленников «De practica geometrie», подходящее дополнение к Liber abbaci.

В 1225 году была издана «Книга квадратов» (Liber quadratorum).В ней рассматривается несколько вопросов теории чисел, среди которых индуктивный метод нахождения пифагоровых троек.

Золотое сечение

Принцип определения размеров золотого сечения лежит в основе совершенства целого мира и его частей в своей структуре и функциях, его проявление можно видеть в природе, искусстве и технике. Учение о золотой пропорции было заложено в результате исследований древними учеными природы чисел.

В основе его лежит теория о пропорциях и соотношениях делений отрезков, которое было сделано еще древним философом и математиком Пифагором. Он доказал, что при разделении отрезка на две части: X (меньшую) и Y (большую), отношение большего к меньшему будет равно отношению их суммы (всего отрезка):

X : Y = Y : X+Y.

В результате получается уравнение: х2 – х – 1=0, которое решается как х=(1±√5)/2.

Если рассмотреть соотношение 1/х, то оно равно 1,618…

Свидетельства использования древними мыслителями золотой пропорции приведены в книге Эвклида «Начала», написанной еще в 3 в. до н.э., который применял это правило для построения правильных 5-угольников. У пифагорейцев эта фигура считается священной, поскольку является одновременно симметричной и асимметричной. Пентаграмма символизировала жизнь и здоровье.

Формула красоты

О золотом сечении говорят, как о формуле идеальной красоты. С детства ребенка учат, что красота и гармония исходит изнутри. Как невидимая и незыблемая сила. Симметрия же тела издавна считалась показателем божественной культуры взрослого или ребенка. О самых красивых людях говорили, что они посланы небесами, божествами. Считалось, что такие люди не столько рождаются, сколько появляются на свет. Современная таблица, учитывающая все пропорции человеческого тела в соответствии с числом ФИ, указывает на вероятные черты идеальной женщины или мужчины.

Симметричны и пропорциональны, такие люди не могут не вызывать любви и восхищения. Красота и безупречность – это только слова. Совершенных людей не бывает. К такому выводу доходят ученые, мыслители и творцы шедевров. К стандарту золотой пропорции дотягиваются единицы, но и у них – творений Бога, найдутся отклонения от формулы сечения. Идеал красоты встречается в природе в виде самых незатейливых формах. Улитка, ушная раковина, семена подсолнуха. Отголоски пропорции Фибоначчи окружают людей изо дня в день. Вот где скрыта истинная красота.

Какие черты человеческого тела считаются максимально пропорциональными? К стандарту красоты причисляются люди с соотношением в размерах:

• высоты и ширины лица;
• длины носа и точки соединение губ;
• расстоянии от точки подбородка к губам и длина всего лица;
• ширины рта и ширина губ;
• расстоянии от одной ноздри к другой и длина всего носа;
• расстоянии между бровями и зрачками.

Стремиться соответствовать правилу золотого сечения неразумно и опасно. Каждый человек – индивидуален, уникален, созданный не по образцу, а как результат миллиона лет эволюции, развития и мутаций. Человек – это венец творения Господа, который ищет ответы на вопросы о собственном происхождении. Пропорции, открытые учеными или математиками, всего-навсего коды, с которыми человек познает не только тело, но и душу.

Расширение на вещественные и комплексные числа

Существует много возможных обобщений, которые расширяют числа Фибоначчи на вещественные числа (а иногда и на комплексные числа). Они используют золотое сечение φ и базируются на формуле Бине

Fn=φn−(−φ)−n5.{\displaystyle F_{n}={\frac {\varphi ^{n}-(-\varphi )^{-n}}{\sqrt {5}}}.}

Аналитическая функция

Fe⁡(x)=φx−φ−x5{\displaystyle \operatorname {Fe} (x)={\frac {\varphi ^{x}-\varphi ^{-x}}{\sqrt {5}}}}

имеет свойство, что Fe(n)=Fn{\displaystyle Fe(n)=F_{n}} для чётных целых чисел n. Аналогично, для аналитической функции

Fo⁡(x)=φx+φ−x5{\displaystyle \operatorname {Fo} (x)={\frac {\varphi ^{x}+\varphi ^{-x}}{\sqrt {5}}}}

выполняется Fo(n)=Fn{\displaystyle Fo(n)=F_{n}} для всех нечётных целых чисел n.

Собирая всё вместе, получим аналитическую функцию

Fib⁡(x)=φx−cos⁡(xπ)φ−x5{\displaystyle \operatorname {Fib} (x)={\frac {\varphi ^{x}-\cos(x\pi )\varphi ^{-x}}{\sqrt {5}}}}

для которой выполняется Fib(n)=Fn{\displaystyle Fib(n)=F_{n}} для всех целых чисел n.

Поскольку Fib(z+2)=Fib(z+1)+Fib(z){\displaystyle Fib(z+2)=Fib(z+1)+Fib(z)} для всех комплексных чисел z, эта функция даёт также расширение последовательности Фибоначчи для всей комплексной плоскости. Таким образом, мы можем вычислить обобщённую функцию Фибоначчи для комплексной переменной, например,

Fib⁡(3+4i)≈−5248,5−14195,9i{\displaystyle \operatorname {Fib} (3+4i)\approx -5248{,}5-14195{,}9i}

Векторное пространство

Термин последовательности Фибоначи может быть применен для любой функции g, отображающей целочисленную переменную в некоторое поле, для которой g(n+2)=g(n)+g(n+1){\displaystyle g(n+2)=g(n)+g(n+1)}. Эти функции в точности являются функциями вида g(n)=F(n)g(1)+F(n−1)g(){\displaystyle g(n)=F(n)g(1)+F(n-1)g(0)}, так что последовательности Фибоначчи образуют векторное пространство, базисом которого являются функции F(n){\displaystyle F(n)} и F(n−1){\displaystyle F(n-1)}.

В качестве области определения функции g может быть взята любая абелева группа (рассматриваемая как Z-модуль). Тогда последовательности Фибоначчи образуют 2-мерный Z-модуль.

Генератор списка

Если мы захотим инициализировать список рядом Фибоначчи, то это можно сделать следующим образом:

def fibonacci(n):
    a, b = 1, 1
    for i in range(n):
        yield a
        a, b = b, a + b

data = list(fibonacci(10))
print(data)

Здесь это генератор объекта ряда размерностью 10. При каждом последующем вызове он будет с помощью возвращать очередной элемент. Мы создаём из него список. Затем выводим список в консоль с помощью функции .

Если нам надо будет поочередно получать числа ряда, а не держать в памяти сразу весь список, то можно поступить следующим образом:

def fibonacci():
    a, b = 1, 1
    while True:
        yield a
        a, b = b, a + b

gen = fibonacci()
for i in range(5):
    print(next(gen))

1
1
2
3
5

Здесь мы создали с помощью Python 3 генератор чисел Фибоначчи. При помощи функции мы получаем поочередно числа ряда.

Что такое золотое сечение

Определение золотому сечению, впервые, дал Евклид в 300 году до н. э. Согласно ему, два объекта находятся в золотой пропорции, если отношение большого объекта к меньшему равно 1.6180.

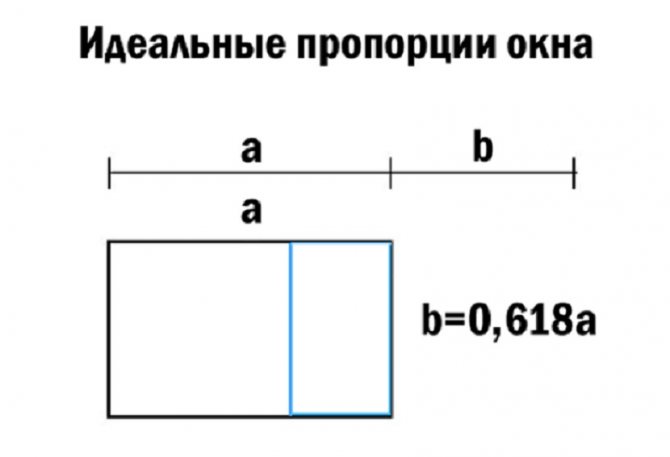
Разделение отрезка на части, согласно золотому сечению Источник www.oknabm.ru

Самое известное применение золотого сечения – золотой прямоугольник. Он содержит в себе другие прямоугольники, при этом каждые соседние по величине прямоугольники, имеют соотношение длины (или ширины) партнера равное 1,618. Эту теорию можно применить и к другим объектам, разделяя их на компоненты таким же способом.

Золотое сечение, также известное как «фи». Его можно продемонстрировать уравнением

а/b=a+b/a=1,618033987, где а больше, чем b.

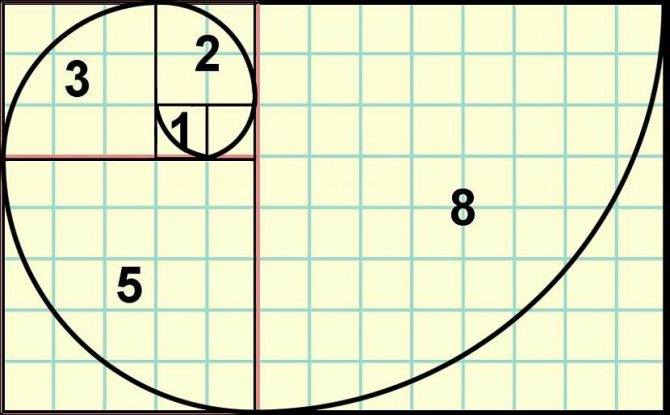
Золотой прямоугольник с соотношение сторон равным золотому сечению Источник www.scienceabc.com

Это явление, также демонстрирует последовательность Фибоначчи

1,1,2,3,5,8,13,21 …

Ряд начинается с 1, и строится таким образом, что каждое следующее число образуется суммой двух предыдущих. Если разделить два соседних числа, то получим результат, приближенный к божественной пропорции — 1,618.

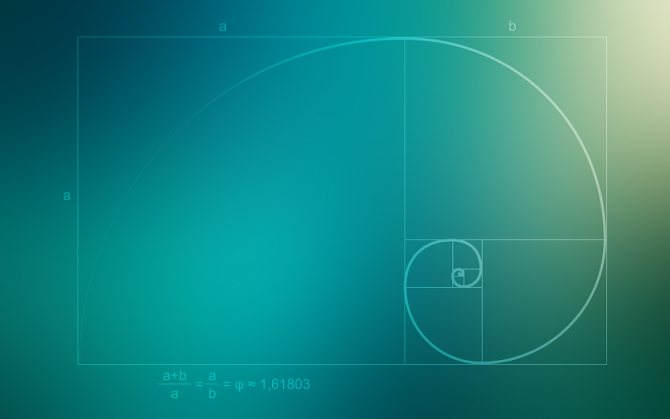
Золотой прямоугольник в который вписана золотая спираль Источник porting-team.ru

Чтобы построить золотую сприраль вам понадобиться золотой прямоугольник, который продемонстрирован на картинке выше. Если у вас есть некоторый набор прямоугольников с соотношением сторон (например, длины и длины), двух соседних по величене квадратов, которая равняеться числу «фи», то вы можете приступить к построению золотой спирали.

Она строиться следующим образом: используя сторону квадрата как радиус вы проводите дугу, которая, двигаясь по диагонали, касается точек квадрата. Продолжайте в том же духе и проводите дугу дальше по всем оставшимся точкам следующих квадратов. Пример такой спирали вы можете увидеть на картинке выше.

Числа Фибоначчи в природе.

Смотреть

А теперь, давайте поговорим о том, как можно опровергнуть то, что цифровой ряд Фибоначчи причастен к каким-либо закономерностям в природе.

Возьмем любые другие два числа и выстроим последовательность с той же логикой, что и числа Фибоначчи. То есть, следующий член последовательности равен сумме двух предыдущих. Для примера возьмем два числа: 6 и 51. Теперь выстроим последовательность, которую завершим двумя числами 1860 и 3009. Заметим, что при делении этих чисел, мы получаем число близкое золотому сечению.

При этом числа, которые получались при делении других пар уменьшались от первых к последним, что позволяет утверждать, что если этот ряд продолжать бесконечно, то мы получим число равное золотому сечению.

Таким образом, числа Фибоначчи ни чем сами по себе не выделяются. Существует другие последовательности чисел, которых бесконечное множество, что дают в результате тех же операций золотое число фи.

Фибоначчи не был эзотериком. Он не хотел вложить никой мистики в числа, он просто решал обыкновенную задачу о кроликах. И написал последовательность чисел, которые вытекали из его задачи, в первый, второй и другие месяца, сколько будет кроликов после размножения. В течение года он получил ту самую последовательность. И не делал отношений. Никакой золотой пропорции, Божественном отношении речи не шло. Все это было придумано после него в эпоху Возрождения.

Перед математикой достоинства Фибоначчи огромны. Он от арабов перенял систему чисел и доказал её справедливость. Была тяжелая и долгая борьба. От римской системы счисления: тяжелой и неудобной для счета. Она исчезла после французской революции. Никакого отношения именно к золотому сечению Фибоначчи не имеет.

Спиралей бесконечно много, наиболее популярны: спираль натурального логарифма, спираль Архимеда, гиперболическая спираль.

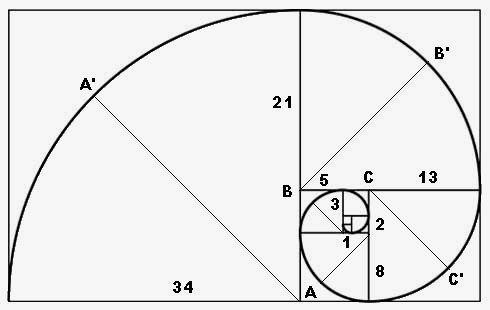
А теперь давайте взглянем на спираль Фибоначчи. Данный кусочно-составной агрегат складывается из нескольких четвертей окружностей. И не является спиралью, как таковой.

Формула для n-го числа Фибоначчи

Формула через радикалы

Существует замечательная формула, называемая по имени французского математика Бине (Binet), хотя она была известна до него Муавру (Moivre):

Эту формулу легко доказать по индукции, однако вывести её можно с помощью понятия образующих функций или с помощью решения функционального уравнения.

Сразу можно заметить, что второе слагаемое всегда по модулю меньше 1, и более того, очень быстро убывает (экспоненциально). Отсюда следует, что значение первого слагаемого даёт «почти» значение . Это можно записать в строгом виде:

где квадратные скобки обозначают округление до ближайшего целого.

Впрочем, для практического применения в вычислениях эти формулы мало подходят, потому что требуют очень высокой точности работы с дробными числами.

Матричная формула для чисел Фибоначчи

Нетрудно доказать матричное следующее равенство:

Но тогда, обозначая

получаем:

Таким образом, для нахождения -го числа Фибоначчи надо возвести матрицу в степень .

Вспоминая, что возведение матрицы в -ую степень можно осуществить за (см. Бинарное возведение в степень), получается, что -ое число Фибоначчи можно легко вычислить за c использованием только целочисленной арифметики.

Почему число Фибоначчи так часто используется в природе?

Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой для образования траекторий движения вихревых потоков в ураганах, при образовании эллиптических галактик, к которым относится и наш Млечный Путь, при «строительстве» раковины улитки или ушной раковины человека, направляет движение косяка рыб и показывает траекторию движения испуганной стаи оленей, врассыпную убегающую от хищника.

Проявление золотого сечения в природе

Эстетичность такой гармонизации мироздания воспринимается человеком, который всегда стремился улучшить окружающую его действительность, в качестве стабилизирующего природу закона. Находя золотое сечение в лице того или иного человека, мы инстинктивно воспринимаем собеседника в качестве гармоничной личности, чье развитие происходит без сбоев и нарушений. Этим можно объяснить то, почему иногда нам по непонятным причинам больше нравится одно лицо, чем другое. Оказывается, о наших возможных симпатиях позаботилась природа!

Наиболее распространенное определение золотого сечения гласит, что меньшая часть так относится к большей, как большая часть относится ко всему целому. Уникальное правило встречается во всех областях природы, науки и искусства, позволив некоторым именитым исследователям Средних Веков сделать предположение, что три основные части золотого сечения олицетворяют собой христианских Отца, Сына и Святого Духа.

Правилу золотого сечения следуют даже галактики. Наш Млечный Путь в этом плане не является исключением

С точки зрения математики, золотое сечение представляет собой некую идеальную пропорцию, к которой каким-то образом стремится все живое и неживое в природе. Используя основные принципы ряда Фибоначчи, растут семечки в центре подсолнуха, движется спираль ДНК, был построен Парфенон и написана самая знаменитая картина в мире — «Джоконда» Леонардо Да Винчи.

Даже коты неосознанно (хотя, кто знает?) следуют принципу золотого сечения, становясь любимцами большей части населения планеты

Есть ли в природе гармония? Несомненно, есть. А ее доказательством служит число Фибоначчи, происхождение которого нам еще только предстоит отыскать.

Использование уровней Фибоначчи в трейдинге

Уровни Фибоначчи помогают установить цели движения цены или найти прогнозируемые области поддержки и сопротивления.

К основным уровням, используемым в трейдинге, относятся: 23.6%, 38.2%, 50%, 61.8%, 78.6%, 100%, 161.8%, 261.8%, 423.6%.

Эти соотношения применяются в различных технических индикаторах, использующих коэффициенты Фибоначчи:

• Коррекции Фибоначчи — горизонтальные линии на графике, которые указывают на области поддержки и сопротивления.
• Расширения Фибоначчи — горизонтальные линии на графике, которые указывают, куда может дойти сильная импульсная волна.
• Дуги Фибоначчи — дугообразные линии, построенные относительно локального максимума или минимума, которые представляют собой области поддержки и сопротивления.
• Веера Фибоначчи — диагональные линии, созданные с использованием максимума и минимума, которые представляют собой области поддержки и сопротивления.
• Временные зоны Фибоначчи — вертикальные линии, отложенные в будущее, предназначенные для предсказания того, когда произойдут основные движения цены.

Коррекции Фибоначчи являются наиболее распространенными формами технического анализа, основанными на последовательности Фибоначчи. Во время тренда можно использовать коррекции, чтобы определить, насколько глубоким может быть откат. Импульсные волны — более крупные волны по направлению тренда, в то время как откаты — это более мелкие волны в противоположную от импульсных волн сторону. Так как они являются меньшими волнами, они будут составлять процент от большей волны.

Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться назад в направлении тренда, у трейдера появится возможность совершить сделку по направлению основного тренда. Трейдеры заранее не знают, какой уровень будет разворотным, поэтому необходимо дождаться уровня, на котором остановится и развернется цена, прежде чем заключать сделку.

Дуги, веера, расширения и временные зоны показывает потенциальные области поддержки или сопротивления, основанные на числах Фибоначчи, относительно предыдущих движений цены. Эти уровни поддержки или сопротивления можно использовать для прогнозирования целей, где цена может развернуться в обратную сторону.

Расширения Фибоначчи можно использовать на любом рынке и на любом таймфрейме. Поскольку уровни расширения могут быть нарисованы на разных таймфреймах, необходимо искать области, где несколько уровней из разных волн сходятся на одной цене

Этот уровень может быть очень важной областью, в которой произойдет разворот цены

Рекурсия

В случае с рекурсией напишем функцию, аргументом которой будет требуемое число ряда Фибоначчи. Текущему значению последовательности вначале присвоим 1. После этого воспользуемся условным оператором языка Python – . В нем проверим аргумент функции. Если он больше 2, то функция вызовет саму себя и вычислит предыдущее значение ряда, а так же то, которое было еще раньше и запишет в переменную их сумму.

def fibonacci(n):
    cur = 1
    if n > 2:
        cur = fibonacci(n-1) + fibonacci(n-2)
    return cur

element = input('Введите номер искомого элемента : ')
element = int(element)
value = fibonacci(element)
print(str(element)+' элемент последовательности равен ' + str(value))

Конечно, пример с рекурсией интересен. Но он будет работать гораздо медленнее.

А если вы решите вычислить, допустим 1000-ый элемент последовательности. Используя цикл, мы его очень быстро рассчитаем. А вот в случае с рекурсией получим ошибку превышения максимального количества рекурсий:

RecursionError: maximum recursion depth exceeded in comparison