Открытые математические проблемы

Массовая щель

Изображение: nnm.me

Математическая теория Янга-Миллса объединяет электромагнитное, сильное и слабое взаимодействие на основе более общей математической теории, связанной с калибровочной симметрией. На основе этих уравнений есть гипотеза о так называемой массовой щели.

В теории относительности частица, которая имеет ненулевую массу покоя, не может двигаться со скоростью света. «Щель» в спектре масс позволяет квантовым частицам иметь конечную ненулевую массу, несмотря на то что связан­ные с ними классические волны движутся со скоростью света.

Эксперименты подтверждают существование массовой щели. Однако этой теории необходимо теоретическое обоснование.

Программирование не только для программистов

Али Партови, предприниматель, сооснователь образовательного некоммерческого проекта Code.org

Нет

15:24

Али Партови тоже считает, что в современном мире без навыков программирования прожить невозможно, поэтому, чем раньше дети научатся общаться с компьютером, тем лучше. На самом деле это гораздо проще, чем кажется, ведь даже в песенках и считалках для самых маленьких можно выделить закономерности и описать их с помощью программ. Али уверен, что, вопреки стереотипам, информатика не превращает человека в компьютерного зомби, а, напротив, расширяет его взгляд на мир, учит мыслить логически и более эффективно решать проблемы. Также не стоит переживать из-за того, что дети останутся без глаз: программы можно писать и на бумаге. В конце концов, первой в мире программисткой считается дочь Байрона Ада Лавлейс — в ее времена, конечно, никаких мониторов не было.

«Давайте поговорим о языке. Мы ведем детей в школу не для того, чтобы они там научились правильно расставлять знаки препинания или освоили орфографию и грамматику. Как только ты научился читать и писать, можно использовать эти навыки, чтобы узнавать что-то новое и, что важнее, чтобы создавать что-то новое и делиться этим. Язык помогает развивать воображение, творческое начало и распространять новые идеи. Но все то же самое можно сказать об информатике. Заниматься информатикой значит не только учиться программировать. Программирование — это лишь начало, совсем как правила орфографии или грамматики. Как только вы освоили язык, оживает ваше воображение, вы можете браться за сложные задачи и создавать нечто новое. Уроки английского готовят детей к колледжу и к жизни, без них невозможно получить высшее образование. То же самое можно сказать о программировании: оно готовит детей к колледжу и к жизни, и при этом практически без разницы, чем они собираются заниматься. Недавно Нобелевскую премию по химии получила команда программистов; в орнитологии, науке о птицах, основные исследования сегодня проводятся программистами

Посмотрим на медицину: один из лучших в мире докторов, глава Института онкологии имени Фреда Хатчинсона, сказал: «Если хочешь стать врачом, то научиться программировать для тебя не менее важно, чем изучить анатомию человека»

Происхождение жизни

Ученые считают, что ключ к пониманию происхождения жизни может быть в выяснении того, как две характерных особенности жизни — размножение и генетическая передача — появились в виде процессов в молекулах, которые получили способность репликации. Это привело к образованию так называемой теории «первичного бульона», согласно которой на юной Земле непонятным образом появилась смесь, этакий бульон из молекул, которая насыщалась энергией солнца и молний. За долгое время эти молекулы должны были сложиться в более сложные органические структуры, из которых состоит жизнь. Эта теория получила частичную поддержку в процессе знаменитого эксперимента Миллера-Ури, когда двое ученых создали аминокислоту, пропуская электрические заряды через смесь простых элементов из метана, аммиака, воды и водорода. Однако открытие ДНК и РНК поумерило изначальный восторг, поскольку кажется невозможным, что такая элегантная структура, как ДНК, сможет развиться из примитивного бульона химических веществ.

Существует течение, которое предполагает, что юный мир был скорее РНК-миром, чем ДНК-миром. РНК, как выяснилось, обладает способностью ускорять реакции, оставаясь неизменной, и хранить генетический материал вместе со способностью к воспроизводству. Но чтобы назвать РНК оригинальным репликатором жизни вместо ДНК, ученые должны найти свидетельства элементов, которые могли образовать нуклеотиды — строительные блоки молекул РНК. Дело в том, что нуклеотиды крайне сложно произвести, даже в лабораторных условиях. Первичный бульон кажется неспособным к произведению этих молекул. Такой вывод привел к другой школе мысли, которая полагает, что органические молекулы, присутствующие в примитивной жизни, обладают внеземным происхождением и были доставлены на Землю из космоса на метеоритах, что привело к развитию теории панспермии. Другое возможное объяснение сводится к теории «железо-серного мира», которая утверждает, что жизнь на Земле образовалась глубоко под водой, вышла из химических реакций, которые происходят в горячей воде под высоким давлением, найденной вблизи гидротермальных источников.

Весьма примечательно, что даже после 200-летней эпохи индустриализации мы до сих пор не знаем, как на Земле появилась жизнь. Впрочем, интерес к этой задаче всегда остается на хорошем температурном уровне.

Квантовая теория гравитации

Разработка теории гравитации

Эта проблема породила новые и любопытные области в физике и математике

Наибольшее внимание привлекла так называемая теория струн. Теория струн заменяет понятие частиц крошечными вибрирующими струнами, которые могут принимать различные формы

Каждая струна может вибрировать определенным образом, который придает ей определенную массу и спин. Теория струн невероятно сложна и математически устроена в десяти измерениях пространства-времени — на шесть больше, чем мы привыкли считать. Эта теория успешно объясняет множество странностей брака гравитации с квантовой механикой и в свое время была устойчивым кандидатом на должность «теория всего».

Другая теория, формулирующая квантовую гравитацию, называется петлевой квантовой гравитацией. ПКГ относительно менее амбициозна и старается быть, прежде всего, уверенной теорией гравитации, не замахиваясь на великое объединение. ПКГ представляет пространство-время как ткань, образованную крошечными петельками, отсюда и названием. В отличие от теории струн, ПКГ не добавляет лишних измерений.

Хотя у обеих теорией есть свои плюсы и минусы, теория квантовой гравитации остается нерешенным вопросом, поскольку ни одна из теорий не была доказана экспериментально. Экспериментальная проверка и подтверждение любой из вышеупомянутых теорией остается гигантской проблемой экспериментальной физики.

Теория квантовой гравитации едва ли возымеет значимый эффект в нашей повседневной жизни, однако, будучи обнаруженной и доказанной, станет мощным свидетельством того, что мы далеко продвинулись в науке и можем двигаться дальше, в направлении физики черных дыр, путешествий во времени и червоточин.

Гипотеза Ходжа

Формулировка этой гипотезы выглядит так: «На любом невырожденном проективном комплексном алгебраическом многообразии любой класс Ходжа представляет собой рациональную линейную комбинацию клас­сов алгебраических циклов». Нужно доказать или опровергнуть это утверждение.

О чем речь? Решения уравнения у = Зх + 1 можно представить на координатной сетке как прямую. Корни квадратного уравнения дадут нам параболу. Усложнять можно бесконечно — например, поверхности с таким уравнением

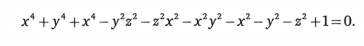
соответствует этот график:

Изображение: Claudio Rocchini / wikipedia.org

Математики не ограничивают себя тремя измерениями. К примеру, в четырехмер­ном пространстве у объекта будет четыре координаты (х, у, z, w). Измерений может быть сколько угодно, число уравнений и переменных тоже может быть любым (не пытайтесь это представить). К тому же переменные могут быть комплексными и принимать бесконечные значения разумным образом.

Гипотеза Ходжа говорит о глубокой связи между топологией, алгеброй, геометрией и анализом. Она предлагает добавить в инструментарий специалиста по алгебраиче­ской геометрии два новых инструмента: топологические инва­рианты и уравнение Лапласа. Если гипотеза верна, эти инструменты обретут новое значение и станут потенциальным средством поиска ответов на множество вопросов.

Равенство классов p и np

Если остальные «Задачи тысячелетия» относятся к чисто математическим, то эта имеет отношение к актуальной теории алгоритмов. Проблема, касающаяся равенства классов р и np, известная также, как проблема Кука-Левина, понятным языком может быть сформулирована следующим образом. Предположим, что положительный ответ на некий вопрос можно проверить достаточно быстро, т. е. за полиномиальное время (ПВ). Тогда правильно ли утверждение, что ответ на него можно довольно быстро отыскать? Еще проще эта задача звучит так: действительно ли решение задачи проверить не труднее, чем его найти? Если равенство классов р и np будет когда-либо доказано, то все проблемы подбора можно будет решать за ПВ. На данный момент многие специалисты сомневаются в истинности этого утверждения, хотя не могут доказать обратное.

Гипотеза о циклах Ходжа

Эта нерешенная до сих пор задача сформулирована в 1941 году. Гипотеза Ходжа предполагает возможность аппроксимации формы любого объекта путем «склеивания» вместе простых тел большей размерности. Этот способ был известен и успешно применяется достаточно давно. Однако не известно, до какой степени можно производить упрощение.

Теперь вы знаете, какие нерешаемые задачи существуют на данный момент. Они являются предметом исследования тысяч ученых во всем мире. Остается надеяться, что в ближайшее время они будут решены, а их практическое применение поможет человечеству выйти на новый виток технологического развития.

Проблемы анализа пространства (геометрия, топология, теория графов — 4)

Геометрия многомерных пространств и гипотеза Пуанкаре

Над гипотезой о вероятных формах Вселенной бились лучшие умы 20 века.

Решение гипотеза Пуанкаре Григорием Перельманом

Российский математик Григорий Перельман решил гипотезу Пуанкаре.
В 2002-2003 годах он совершил прорыв, предложив ряд новых идей.
Он развил и довел до конца метод, предложенный в 1980-е годы Ричардом Гамильтоном.
В своих работах Перельман утверждает, что построенная им теория позволяет доказать не только гипотезу Пуанкаре,
но и гипотезу геометризации Тёрстона.

Суть метода состоит в том, что для геометрических объектов можно определить некоторое уравнение «плавной эволюции»,
похожее на уравнение ренормализационной группы в теорфизике.
Исходная поверхность в ходе этой эволюции будет деформироваться и, как показал Перельман,
в конце концов плавно перейдет именно в сферу.
Сила этого подхода состоит в том, что, минуя все промежуточные моменты, можно сразу заглянуть «в бесконечность»,
в самый конец эволюции, и обнаружить там сферу.

В  2002 году Г. Перельман опубликовал решение гипотезы Пуанкаре,
и до сих пор ни один пристрастный анализ не нашел в нем ошибки.

Топология и гипотеза Ходжа

Гипотеза Ходжа сформулирована в 1941 году и состоит в том, что для особенно хороших типов пространств,
называемых проективными алгебраическими многообразиями, так называемые циклы Ходжа являются комбинациями объектов,
имеющих геометрическую интерпретацию, — алгебраических циклов.

В XX веке математики изобрели мощные методы исследования формы сложных объектов.
Основная идея состоит в том, чтобы выяснить, до какой степени мы можем аппроксимировать форму данного объекта,
склеивая вместе простые тела возрастающей размерности.
Этот метод оказался эффективным при описании разнообразных объектов встречающихся в математике.
При этом были не ясны геометрические обоснования метода: в некоторых случаях было необходимо прибавлять части,
которые не имели никакого геометрического истолкования.

Доказать гипотезу Ходжа удалось для некоторых частных случаев. Более общее доказательство пока не найдено,
не найдено и доказательство обратного — что гипотеза неверна.

Проблемы 2000 года: гипотеза Ходжа.

Квантовая физика и геометрия (гипотеза Янга-Миллса)

Тео́рия Я́нга—Ми́ллса — калибровочная теория с неабелевой калибровочной группой.
Калибровочные поля в этой теории называются полями Янга — Миллса.
Такие теории были предложены в 1954 году Чж. Янгом (Yang) и Р. Миллсом (Mills),
однако долгое время рассматривались лишь как математические изыски, не имеющие отношения к реальности.

Несмотря на это, именно на основе теорий Янга — Миллса в 1970-х годах были созданы
две краеугольные теории Стандартной Модели в физике элементарных частиц:
квантовая хромодинамика (теория сильных взаимодействий) на основе группы SU(3)
и теория электрослабых взаимодействий на основе группы SU(2).

Теория Янга-Миллса.

Теория графов и теорема Шварца-Кристоффеля

Теорема Шварца — Кристоффеля относится к теории функций комплексного переменного
и носит название немецких математиков Карла Шварца и Элвина Кристоффеля.

Она касается проблемы о конформном отображении некой канонической области (единичного круга Δ или верхней полуплоскости H+)
на внутренность произвольного многоугольника

Теорема дает общий вид таких отображений, что важно с практической точки зрения.. Сформулированная 140 лет назад формула Шварца–Кристоффеля является незаменимой для проектирования различных объектов,
включая здания, мосты, а также самолеты

Она определяет уровень внешней и внутренней сопротивляемости структуры и степень запаса ее прочности. Однако классическая формула не могла быть применена для сложных объектов, имеющих отверстия и сложные формы

Сформулированная 140 лет назад формула Шварца–Кристоффеля является незаменимой для проектирования различных объектов,
включая здания, мосты, а также самолеты.
Она определяет уровень внешней и внутренней сопротивляемости структуры и степень запаса ее прочности.
Однако классическая формула не могла быть применена для сложных объектов, имеющих отверстия и сложные формы.

• Доказательства великих завихрений.

Как Вы можете помочь?

Если проблемы с исполнительными функциями стоят на пути изучения математики у Вашего ребенка, ему можно помочь преодолеть их с помощью различных методов.

Начните с того, что приучите его вчитываться в задачу, прежде чем приступать к ее решению. Пусть он подчеркивает вопросы и выделяет маркером важные пункты (включая знаки «плюс» и «минус»). Он должен оценить, знает ли он, как решить проблему и нужна ли ему помощь. Пусть задаст себе вопросы, вроде «чем похожа и чем отличается эта задача он предыдущей?».

​

Помогите ребенку создать свой собственный список того, на что ему нужно обратить внимание прежде, чем сдать работу на проверку. Научите его самостоятельно проверять свою работу и выявлять ошибки

​

​

​

​

Вот то, что нужно помнить, помогая ребёнку с трудной домашней работой по математике:

​

1. Для начала, непонимание чего-либо сильно действует на нервы. Поддержите ребёнка и пресекайте весь негатив, который возникает в процессе работы.

2. Попросите ребёнка показать примеры задачи. Например, похожую задачу, которую они решали в классе или пример из учебника, к которому прилагается правильный ответ.

3. Если Ваш ребёнок не нашёл примера задачи, попытайтесь найти помощь в интернете. В учебнике Вашего ребёнка есть заголовки или какие-то ключевые слова, по которым можно найти статьи или примеры задач в интернете. Попробуйте несколько сайтов, в них наверняка подробно написано, как решать подобные задачи. 

4. После того, как Вы найдёте пример задачи, спросите у ребенка, как ее решал учитель. Имея перед глазами решённый пример, ребёнок может вспомнить, как учитель решал задачу.

5. Используйте пример задачи, чтобы понять, как пошагово решить ее. Запишите каждый шаг, который помнит Ваш ребёнок, решая вместе первую задачу. Это напомнит Вашему ребёнку, что математика — это процесс. Записывая рассуждения за Вашим ребёнком, Вы создадите список, который ребёнок может отдать учителю, чтобы показать, что он старался, даже если у него ничего не вышло. Используя этот список, учитель может объяснить, где именно ребёнок ошибся, чтобы в будущем он смог решить эту задачу. 

Предыстория

В 1900 году великий немецкий математик-универсал Дэвид Гильберт, представил список из 23-х проблем.

Исследования, осуществленные с целью их решения, оказали огромное влияние на науку 20 века. На данный момент большинство из них уже перестали быть загадками. В числе нерешенных или решенных частично остались:

• проблема непротиворечивости арифметических аксиом;
• общий закон взаимности на пространстве любого числового поля;
• математическое исследование физических аксиом;
• исследование квадратичных форм при произвольных алгебраических числовых коэффициентах;
• проблема строгого обоснования исчислительной геометрии Федора Шуберта;
• и пр.

Неисследованными являются: проблема распространения на любую алгебраическую область рациональности известной теоремы Кронекера и гипотеза Римана.

Гипотеза Римана

Вплоть до 1859 года не было выявлено какой-либо закономерности, которая описывала бы, как распределяются простые числа среди натуральных. Возможно, это было связано с тем, что наука занималась другими вопросами. Однако к середине 19 столетия ситуация изменилась, и они стали одними из наиболее актуальных, которыми начала заниматься математика.

Гипотеза Римана, появившаяся в этот период — это предположение о том, что в распределении простых чисел существует определенная закономерность.

Сегодня многие современные ученые считают, что если она будет доказана, то придется пересмотреть многие фундаментальные принципы современной криптографии, составляющие основу значительной части механизмов электронной коммерции.

Согласно гипотезе Римана, характер распределения простых чисел, возможно, существенно отличается от предполагаемого на данный момент. Дело в том, что до сих пока не было обнаружено какой-либо системы в распределения простых чисел. Например, существует проблема «близнецов», разность между которыми равна 2. Этими числами являются 11 и 13, 29. Другие простые числа образуют скопления. Это 101, 103, 107 и др. Ученые давно подозревали, что подобные скопления существуют и среди очень больших простых чисел. Если их найдут, то стойкость современных криптоключей окажется под вопросом.

Фолдинг белка

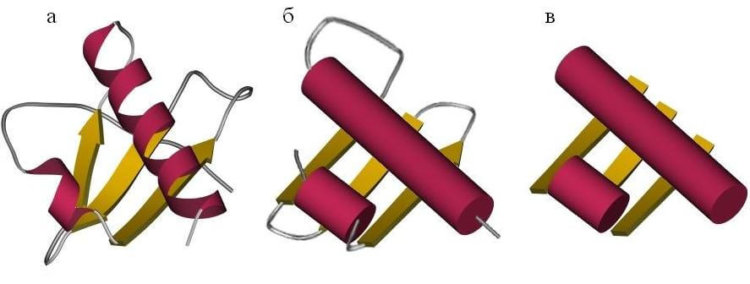
В процессе фолдинга задействовано большое количество сил и взаимодействий, которые позволяют белку достичь состояния самой низкой из возможных энергий, что придает ему стабильность. Из-за большой сложности структуры и большого количества вовлеченных силовых полей, довольно трудно понять точную физику процесса фолдинга небольших белков. Проблему прогнозирования структуры пытались решить в комбинации с физикой и мощными компьютерами. И хотя с небольшими и относительно простыми белками был достигнут определенный успех, ученые до сих пор пытаются точно спрогнозировать сложенную форму сложных многодоменных белков по их аминокислотной последовательности.

Чтобы понять процесс, представьте, что находитесь на перекрестке тысячи дорог, которые ведут в одном направлении, и вам нужно выбрать путь, который приведет вас к цели за наименьшее время. Точно такая же, только более масштабная проблема лежит в кинетическом механизме фолдинга белка в определенное состояние из возможных. Было выяснено, что случайные тепловые движения играют большую роль в быстрой природе фолдинга и что белок «пролетает» через конформации локально, избегая неблагоприятные структуры, но физический путь остается открытым вопросом — и его решение может привести к появлению более быстрых алгоритмов прогнозирования структуры белка.

Проблема фолдинга белка остается горячей темой в биохимических и биофизических исследованиях современности. Физика и вычислительные алгоритмы, разработанные для фолдинга белка, привели к разработке новых искусственных полимерных материалов. Помимо вклада в рост научных вычислений, проблема привела к лучшему пониманию заболеваний вроде диабета II типа, Альцгеймера, Паркинсона и Хантингтона — в этих расстройствах неправильный фолдинг белков играет важную роль. Лучшее понимание физики фолдинга белка может не только привести к прорывам в материаловедении и биологии, но и произвести революцию в медицине.

Другие важные задачи математики

Обзоры. статьи и новости о других важных математических проблемах и задачах:
проблемах Гилберта, теореме Атия-Сингера…

ABC-гипотеза (гипотеза Эстерле-Массера)

Независимо друг от друга abc-гипотеза предложена математиками
Дэвидом Массером в 1985 году и Джозефом Эстерле в 1988 году.
Ее решение составляет одну из главных проблем теории чисел.
Гипотеза утверждает, что для любого действительного числа r > 1 существует не более конечного числа
троек натуральных чисел a, b и c таких, что для них выполняются условия: a + b = c;
a, b и c взаимно просты в совокупности (то есть у них нет общих делителей) и c > rad(abc)r.

Радикалом (rad) натурального числа N называется число, которое представляет собой произведение
всех различных простых (отличных от единицы чисел, делящихся только на себя и на единицу) делителей числа N.
Например, rad (15) = 15, так как у этого числа простые делители 3 и 5,
а rad (18) = 6, поскольку простых делителей у числа 18 ровно два — это 3 и 2.

Гипотеза Эстерле-Массера важна для теории диофантовых уравнений, а ее справедливость
позволит провести еще одно доказательство великой теоремы Ферма для больших степеней.

И вот, в 2012 году японский математик Синъити Мотидзуки представил доказательство abc-гипотезы,
которое занимает более 500 страниц текста. Понять и проверить его способно небольшое число математиков.
У эксперта может уйти до 500 часов работы для понимания доказательства,
тогда как у математика-аспиранта это займет около 10 лет.
В настоящее время проверкой работы Мотидзуки занимаются десять математиков.
Отдельные этапы доказательства математика ясны, но «всеобъемлющая стратегия остается совершенно неуловимой».
Считается, что проверить корректность доказательства Мотидзуки удастся к 2017 году,

Работа японского ученого содержит революционные идеи и использует оригинальные обозначения,
ранее не встречавшиеся в математической литературе.

Доказательство «японского Перельмана» совершило революцию в математике.

Атия-Сингера теорема

Теорема Атьи — Зингера об индексе — один из наиболее популярных математических результатов последнего пятилетия.
Такой интерес к проблеме индекса объясняется ее положением на стыке анализа и топологии,
а также тем, что для ее решения потребовались новейшие математические разработки.

Пале. Р. Семинар по теореме Атьи — Зингера об индексе.

Гильберта проблемы

Пробле́мы Ги́льберта — список из 23 кардинальных проблем математики, представленный Давидом Гильбертом
на II Международном Конгрессе математиков в Париже в 1900 году.
Тогда эти проблемы (охватывающие основания математики, алгебру, теорию чисел, геометрию,
топологию, алгебраическую геометрию, группы Ли, вещественный и комплексный анализ,
дифференциальные уравнения, математическую физику и теорию вероятностей, а также вариационное исчисление) не были решены.

Новости о «неключевых», но важных математических достижениях

Высшей награды в области математики удостоена работа 40-летней давности.

Высшая награда в области математики — норвежская Премия Абеля – присуждена двум ученым:
британцу сэру Майклу Фрэнсису Атьи и Айсадору М. Зингеру из США за работу на стыке двух наук – физики и математики.
Норвежская Академия наук и литературы выделила 6 млн крон «за их открытие и доказательство теоремы об индексе
с помощью топологии, геометрии и математического анализа,
а также за их выдающуюся роль в создании новых связей между математикой и теоретической физикой».
75-летний Атья из университета Эдинбурга и 79-летнйи Зингер из технологического института Массачусетса
еще 40 лет назад разработали то, что сейчас называется теоремой Атия-Сингера.

Главная

Математика:
Арифметика и ТЧ |
Геометрия |
Алгебра |
Матанализ |
Дискретная математика |
Прикладная математика |
Проблемы математики

Близкие по теме страницы:
Гранты |
Эвристика и авторство |
Информатика

На правах рекламы (см.
условия):

Страница обновлена 11.09.2020

Институт Клэйя

Под таким названием известна частная некоммерческая организация, штаб-квартира которой находится в Кембридже, штат Массачусетс. Она была основана в 1998 году гарвардским математиком А. Джеффи и бизнесменом Л. Клэйем. Целью деятельности института является популяризация и развитие математических знаний. Для ее достижения организация выдает премии ученым и спонсирует многообещающие исследования.

В начале 21 столетия Математический институт Клэйя предложил премию тем, кто решит проблемы, которые известны, как самые сложные нерешаемые задачи, назвав свой список Millennium Prize Problems. Из «Списка Гильберта» в него вошла только гипотеза Римана.