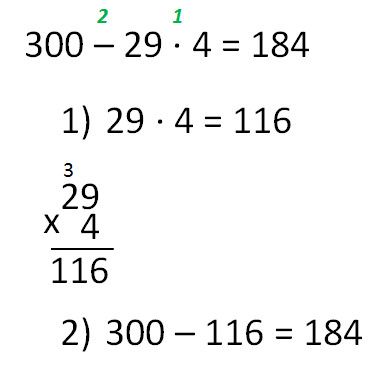Основные арифметические действия

Содержание:

Основные темы
Примеры решения задач
Десятичная арифметика
Порядок выполнения арифметических действий в выражениях со скобками
Интегральное исчисление
Арифметика составных единиц
Третий закон Ньютона
Разряды чисел

Основные темы

Количество

Основной раздел, рассматривающий абстракцию количества — алгебра. Понятие «число» первоначально зародилось из арифметических представлений и относилось к натуральным числам. В дальнейшем оно, с помощью алгебры, было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.

1,2,…{\displaystyle 1,\;2,\;\ldots }

Натуральные числа

,1,−1,…{\displaystyle 0,\;1,\;-1,\;\ldots }

Целые числа

1,−1,12,23,,12,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;{\frac {2}{3}},\;0{,}12,\;\ldots }

Рациональные числа

1,−1,12,,12,π,2,…{\displaystyle 1,\;-1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;{\sqrt {2}},\;\ldots }

Вещественные числа

−1,12,,12,π,3i+2,eiπ3,…{\displaystyle -1,\;{\frac {1}{2}},\;0{,}12,\;\pi ,\;3i+2,\;e^{i\pi /3},\;\ldots }

1,i,j,k,πj−12k,…{\displaystyle 1,\;i,\;j,\;k,\;\pi j-{\frac {1}{2}}k,\;\dots }

Комплексные числа

Кватернионы

Числа — Натуральные числа — Целые числа — Рациональные числа — Иррациональные числа — Алгебраические числа — Трансцендентные числа — Вещественные числа — Комплексные числа — Гиперкомплексные числа — Кватернионы — Октонионы — Седенионы — Гиперреальные числа — Сюрреальные числа — p-адические числа — Математические постоянные — Названия чисел — Бесконечность — Базы

Преобразования

Явления преобразований и изменений в самом общем виде рассматривает анализ.

36÷9=4{\displaystyle 36\div 9=4}			∫1Sdμ=μ(S){\displaystyle \int 1_{S}\,d\mu =\mu (S)}
Арифметика	Дифференциальное и интегральное исчисление	Векторный анализ	Анализ
d2dx2y=ddxy+c{\displaystyle {\frac {d^{2}}{dx^{2}}}y={\frac {d}{dx}}y+c}
Дифференциальные уравнения	Динамические системы	Теория хаоса

Арифметика — Векторный анализ — Анализ — Теория меры — Дифференциальные уравнения — Динамические системы — Теория хаоса

Структуры

Теория множеств — Линейная алгебра — Общая алгебра (включает, в частности, теорию групп, универсальную алгебру, теорию категорий) — Алгебраическая геометрия — Теория чисел — Топология.

Пространственные отношения

Основы пространственных отношений рассматривает геометрия. Тригонометрия рассматривает свойства тригонометрических функций. Изучением геометрических объектов посредством математического анализа занимается дифференциальная геометрия. Свойства пространств, остающихся неизменными при непрерывных деформациях и само явление непрерывности изучает топология.


Геометрия	Тригонометрия	Дифференциальная геометрия	Топология	Фракталы	Теория меры

Геометрия — Тригонометрия — Алгебраическая геометрия — Топология — Дифференциальная геометрия — Алгебраическая топология — Линейная алгебра — Фракталы — Теория меры.

Дискретная математика

Дискретная математика включает средства исследования объектов, способных принимать только отдельные (дискретные) значения (то есть объектов, не способных изменяться плавно).

∀x(P(x)⇒P(x′)){\displaystyle \forall x(P(x)\Rightarrow P(x’))}
Математическая логика	Теория вычислимости	Криптография	Теория графов

Комбинаторика — Теория множеств — Теория решёток — Математическая логика — Теория вычислимости— Криптография — Теория функциональных систем — Теория графов — Теория алгоритмов — Логические исчисления
— Информатика.

Примеры решения задач

Что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации

Задача 1.

Теоретическое введение

Функцией переменной величины , называется величина такая, что каждому значению , принадлежащей некоторой области , соответствует единственное значение величины .

Обозначение: .

– область определения функции, – аргумент.

– область изменения функции, – значение;

Функция может быть задана аналитически, таблично, графически.

Основными элементарными функциями являются:

1. степенные (, где – произвольное число)

показательные (, , )
логарифмические (,, )
тригонометрические (, , , )
обратные тригонометрические (,,, )

Композиция (суперпозиция) двух функций и есть функция, в которой аргументом одной из данных функции, является значение другой функции. Обозначение: и .

Сложная функция есть композиция двух и более функций.

Элементарная функция есть функция, полученная из основных элементарных функций с помощью арифметических действии и композиции.

Целью математического анализа является изучение различных функций, их свойств, и операций связанных с функциями.

Функция называется четной, если для всех своих аргументов.

Функция называется нечетной, если для всех своих аргументов.

Число называется пределом функции при , стремящемся к и обознается , если при неограниченном приближении к , неограниченно приближается .

Свойства пределов:

Передел суммы двух функций равен сумме пределов этих функций, если они существуют:
Предел произведения функции равен произведению пределов, если они существуют:
Предел частного двух функций равен частному пределов, если они существуют, и предел знаменателя не равен нулю: , при .

Обычно , например:

Однако, иногда значение не входит в область определения функции . В этом случае имеются различные методы вычисления пределов:

Выделение общего множителя

Выделение главной части

Использование замечательных пределов

Первый замечательный предел:

Второй замечательный предел:

Задача 2.

Теоретическое введение

Производная или от данной функции есть предел отношения приращения функции к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю: или

Механический смысл производной – скорость изменения функции.

Геометрический смысл производной – тангенс угла наклона касательной к графику функции:

Правила дифференцирования:

Производная постоянной величины равна 0.
Производная суммы равна сумме производных.
Производная произведения:
Производная частного:

Производная сложной функции:

Производная от сложной функции по независимому аргументу равна производной от по промежуточному аргументу , умноженной на его производною по независимой переменной .

Примеры:

;
;
;

Задача 4.

Найти неопределенные интегралы:

а) ;

Решение: введем переменную . Тогда ; . Сделаем замену:

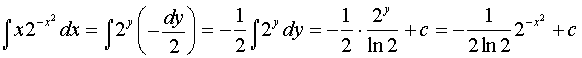б) ;

Решение: используем метод интегрирования по частям:

Обозначим: . Тогда .

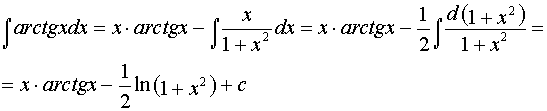
Задача 5.

Вычислить площадь фигуры, ограниченной линиями:

и .

Решение:

Найдем точки пересечения графиков данных функций. Для этого приравняем функции и решим уравнение

Итак, точки пересечения и .

Площадь фигуры найдем, используя формулу

В нашем случае

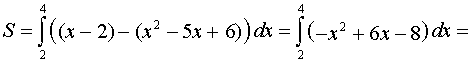
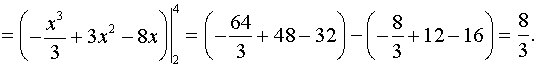
Ответ: площадь равна (квадратных единиц).

Десятичная арифметика

Какие наши дальнейшие действия?

Десятичное представление обычно относится исключительно к письменной системе счисления, в которой арабские цифры используются в качестве цифр для позиционной системы счисления с основанием 10 («десятичная») ; тем не менее, любую систему счисления, основанную на степени 10, например греческие , кириллические , римские или китайские числа, можно концептуально описать как «десятичное представление» или «десятичное представление».

Современные методы для четырех основных операций (сложение, вычитание, умножение и деление) были впервые изобретены Брахмагуптой из Индии. В средневековой Европе это было известно как «Modus Indoram» или метод индейцев. Позиционное обозначение (также известное как «обозначение разряда») относится к представлению или кодированию чисел с использованием одного и того же символа для разных порядков величины (например, «разряды единиц», «разряды десятков», «разряды сотен») и, с точкой счисления , использование тех же символов для представления дробей (например, «десятые доли», «сотые доли»). Например, 507,36 означает 5 сотен (10 2 ), плюс 0 десятков (10 1 ), плюс 7 единиц (10 ), плюс 3 десятых (10 -1 ) плюс 6 сотых (10 -2 ).

Концепция как числа, сравнимого с другими основными цифрами, важна для этого обозначения, как и концепция использования 0 в качестве заполнителя, а также определение умножения и сложения с 0. Использование 0 в качестве заполнителя и Таким образом, использование позиционного обозначения впервые засвидетельствовано в джайнском тексте из Индии под названием Локавибхага , датируемом 458 г. н.э., и только в начале 13 века эти концепции, переданные через научные исследования арабского мира , были введены в Европу по Фибоначчи с использованием индийско-арабской системы счисления.

Алгоризм включает в себя все правила выполнения арифметических вычислений с использованием этого типа письменных чисел. Например, сложение дает сумму двух произвольных чисел. Результат вычисляется путем повторного сложения одиночных цифр из каждого числа, занимающего одну и ту же позицию, начиная справа налево. В таблице сложения с десятью строками и десятью столбцами отображаются все возможные значения для каждой суммы. Если индивидуальная сумма превышает значение 9, результат представляется двумя цифрами. Самая правая цифра — это значение для текущей позиции, а результат последующего сложения цифр слева увеличивается на значение второй (самой левой) цифры, которая всегда равна единице (если не нулю). Эта корректировка называется переносом значения 1.

Процесс умножения двух произвольных чисел аналогичен процессу сложения. В таблице умножения с десятью строками и десятью столбцами перечислены результаты для каждой пары цифр. Если отдельное произведение пары цифр превышает 9, корректировка переноса увеличивает результат любого последующего умножения цифр слева на значение, равное второй (крайней левой) цифре, которая представляет собой любое значение от 1 до 8 ( 9 × 9 = 81 ). Дополнительные шаги определяют конечный результат.

Подобные методы существуют для вычитания и деления.

Создание правильного процесса умножения зависит от отношения между значениями соседних цифр. Значение любой отдельной цифры в цифре зависит от ее положения. Кроме того, каждая позиция слева представляет собой значение, в десять раз превышающее позицию справа. С математической точки зрения, показатель степени для системы счисления (основания) 10 увеличивается на 1 (слева) или уменьшается на 1 (справа). Следовательно, значение любой произвольной цифры умножается на значение формы 10 n с целым числом n . Список значений, соответствующих всем возможным позициям одной цифры, записывается как {…, 10 2 , 10, 1, 10 −1 , 10 −2 , …}.

Повторное умножение любого значения в этом списке на 10 дает другое значение в списке. В математической терминологии эта характеристика определяется как замыкание , а предыдущий список описывается как закрытый при умножении . Это основа для правильного нахождения результатов умножения с использованием предыдущей техники. Этот результат — один из примеров использования теории чисел .

Порядок выполнения арифметических действий в выражениях со скобками

Какие действия могут счесть государственной изменой

Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2.

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

Ответ:

5+(7−2·3)·(6−4):2=6.

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)).

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.

Ответ:

4+(3+1+4·(2+3))=28.

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.

Интегральное исчисление

Основные определения

Функция называется первообразной для функции , если .

Т.1: Если и — первообразные для , то

Доказательство:

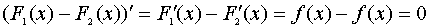; ЧТД.

Неопределенным интегралом от называется класс всех первообразных для .

— подынтегральная функция.

— дифференциал.

— переменная интегрирования.

Для любой непрерывной функции существует первообразная.

3.2. Таблица интегралов

10.

11.

12.

13.

Доказательство каждого из табличных интегралов осуществляется с помощью дифференцирования (по определению). Например, для 10 и 11 табличных интегралов:

Доказательство:

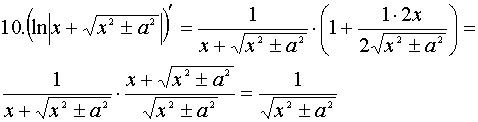
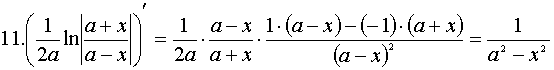
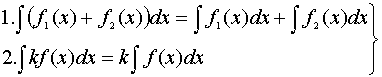— линейность

Следствие:

1.;

Замена переменных под знаком неопределенного интеграла

Интегрирование по частям.

Доказательство:

(формула дифференцирования произведения).

(интегрируем обе части равенства)

(использование основного тождества)

(что и требовалось доказать).

Пример:

1) (замена переменной)

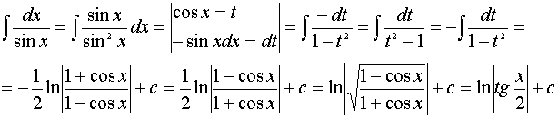
2) (интегрирование по частям)

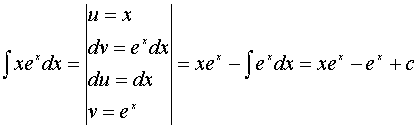
Интегрирование рациональных дробей. Простейшие дроби и их интегрирование

Все коэффициенты действительные числа.

m , n – целые числа.

Нет общих корней.

Если , то дробь называется неправильной, если , то дробь называется правильной.

Если дробь неправильная, то , где — правильная дробь; — многочлен.

Простейшие дроби:

2. , и целое число.

3. ( в знаменателе неприводимый квадратный трехчлен).

4. , и целое число.

= = = = = =

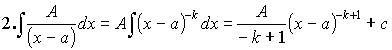
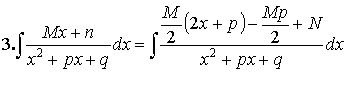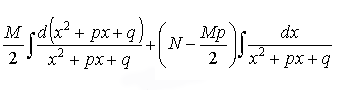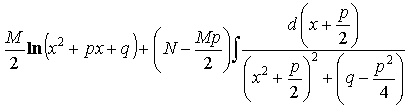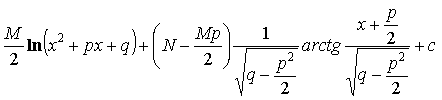
Разложить рациональные дроби на простейшие

Теорема. Если х = а – корень знаменателя f(x) кратности k , то

Доказательство:

; (1)

Будем подбирать А так, чтобы По теореме Безу это возможно, если

Тогда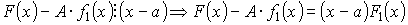

Подставим в (1)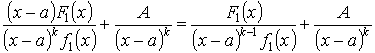

Следствие:

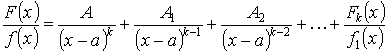
Теорема. Если ( — неприводимый квадратный трехчлен. 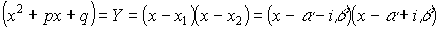), то

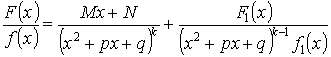
Доказательство:

Подберем M и N так, чтобы числитель делился на Y : 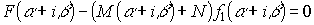— по теореме Безу.

M и N можно найти из этой системы всегда.

Следствие: всякая правильная рациональная дробь может быть разложена в сумму простейших дробей.

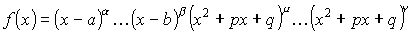
Пример:

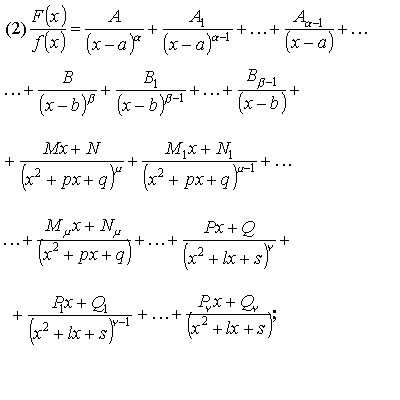
Метод неопределенных коэффициентов

Правую часть равенства (2) надо привести к общему знаменателю и приравнять в числители коэффициенты при одинаковых степенях F(x). Решая полученную систему уравнений можно определить все коэффициенты.

Интегрирование рациональных дробей

Выделить целую часть дроби.
Разложить знаменатель на множители.
Представить в виде суммы простейших дробей.
Найти неопределенные коэффициенты.
Интегрировать каждую простейшую дробь.

Интегрирование иррациональных функций

3.3.1.

k – общий знаменатель дробей

— рационализирующая подстановка.

Пример: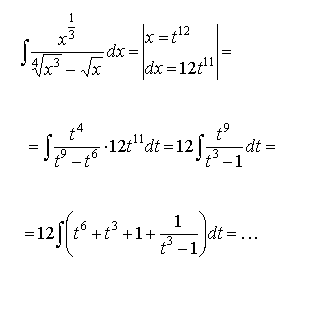

3.3.2.

k – общий знаменатель дробей

Пример:

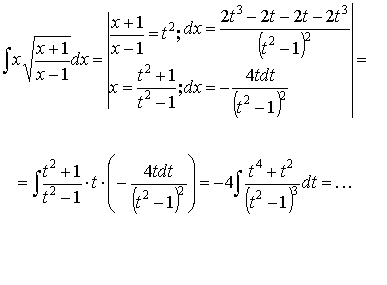
3.3.3. Тригонометрические подстановки.

Пример: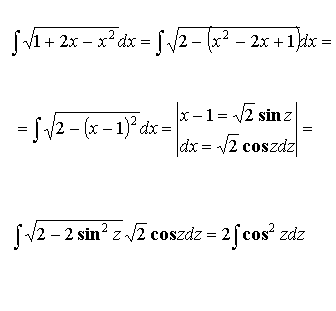

— обратные гиперболические функции.

Определение и свойства

S – область – криволинейная трапеция.

Интегральная сумма: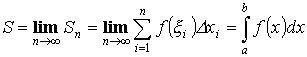

Определенным интегралом называется предел интегральной суммы.

Теорема. “О существовании определенного интеграла”

Если f(x) – непрерывна на отрезке (a,b), то определенный интеграл существует и не зависит от порядка разбиения и выбора точек.

Геометрический смысл определенного интеграла – площадь криволинейной трапеции.

Свойства определенного интеграла:

1. — аддитивность.
2. на

Пусть y =f(x) интегрируема на Тогда

Доказательство:

Теорема 2. “о среднем”

Пусть y =f(x) интегрируема на Тогда — где f(c) – среднее значение f(x) на .

Доказательство:

По Т.1:

Т.к. f(x) – непрерывна на , то она принимает все промежуточные значения от m до M. Следовательно она принимает значение А. Т.е. существует такая

Пусть y =f(x) — интегрируема на . Тогда

Доказательство:

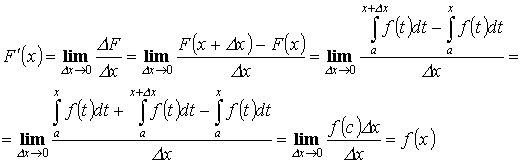
Теорема 4. “формула Ньютона-Лейбница”

, где F(x) – первообразная для f(x).

Доказательство:

— первообразная для f(x) по Т.3. Т.к. первообразные отличаются на const, то Пусть х=а. F(a)+c=0. c=-F(x). Пусть x=b

Методы вычисления определенного интеграла

Замена переменных под знаком определенного интеграла.

Пример:

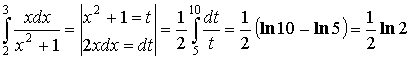
Интегрирование по частям в определенном интеграле.

Пример:

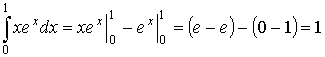
— из определения

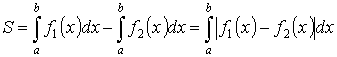
Пример:

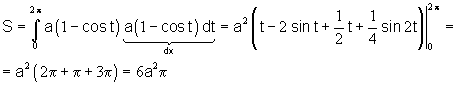
Арифметика составных единиц

Арифметика составных единиц — это применение арифметических операций к смешанным системам счисления, таким как футы и дюймы; галлоны и пинты; фунты, шиллинги и пенсы; и так далее. До появления десятичных систем денег и единиц измерения сложная арифметика единиц широко использовалась в торговле и промышленности.

Основные арифметические операции

Методы, используемые в арифметике составных единиц, разрабатывались на протяжении многих веков и хорошо документированы во многих учебниках на разных языках. В дополнение к основным арифметическим функциям, встречающимся в десятичной арифметике, арифметика составных единиц использует еще три функции:

Сокращение , при котором сложное количество сокращается до единственной величины — например, преобразование расстояния, выраженного в ярдах, футах и дюймах, в расстояние, выраженное в дюймах.
Расширение , функция, обратная уменьшению, представляет собой преобразование количества, выраженного как единая единица измерения, в составную единицу, например, увеличение 24 унций до 1 фунта 8 унций .
Нормализация — это преобразование набора составных единиц в стандартную форму, например, переписывание « 1 фут 13 дюймов » на « 2 фут 1 дюйм ».

Знание взаимосвязи между различными единицами измерения, их кратными и их частными кратными составляет важную часть арифметики составных единиц.

Принципы арифметики составных единиц

Существует два основных подхода к арифметике составных единиц:

Метод редукции – расширения, при котором все переменные составных единиц сводятся к переменным единичных единиц, выполняется вычисление и результат возвращается к составным единицам. Этот подход подходит для автоматизированных расчетов. Типичным примером является обработка времени в Microsoft Excel, где все временные интервалы обрабатываются внутри как дни и десятичные дроби дня.
Метод непрерывной нормализации, при котором каждая единица рассматривается отдельно, а проблема непрерывно нормализуется по мере развития решения. Этот подход, широко описанный в классических текстах, лучше всего подходит для расчетов вручную. Пример продолжающегося метода нормализации применительно к сложению показан ниже.

Десятичная валюта Великобритании
4 фартинга (f) = 1 пенни
12 пенни (d) = 1 шиллинг
20 шиллингов = 1 фунт (£)

Операция сложения выполняется справа налево; в этом случае сначала обрабатываются пенсы, затем шиллинги, а затем фунты. Цифры под «линией ответа» являются промежуточными результатами.

Сумма в столбце пенсов равна 25. Поскольку в шиллинге 12 пенни, 25 делится на 12, чтобы получить 2 с остатком 1. Затем значение «1» записывается в строку ответа, а значение «2». перенесены в колонку шиллингов. Эта операция повторяется с использованием значений в столбце шиллингов с дополнительным шагом добавления значения, перенесенного из столбца пенни. Промежуточная сумма делится на 20, так как в фунте 20 шиллингов. Затем обрабатывается столбец фунтов, но поскольку фунты являются самой большой рассматриваемой единицей, значения из столбца фунтов не переносятся.

Для простоты в выбранном примере не было фартингов.

Операции на практике

Шкала, откалиброванная в имперских единицах, с соответствующим дисплеем стоимости.

В течение 19 и 20 веков были разработаны различные вспомогательные средства, помогающие манипулировать составными единицами, особенно в коммерческих приложениях. Самыми распространенными вспомогательными средствами были механические кассы, адаптированные в таких странах, как Соединенное Королевство, для размещения фунтов, шиллингов, пенни и фартингов, а также «Готовые счетчики» — книги, предназначенные для трейдеров, которые каталогизировали результаты различных рутинных расчетов, таких как проценты или кратные различных денежных сумм. В одном типичном буклете объемом 150 страниц в таблице были кратные «от одной до десяти тысяч по разным ценам от одного фартинга до одного фунта».

Громоздкость арифметики составных единиц была признана в течение многих лет — в 1586 году фламандский математик Саймон Стевин опубликовал небольшую брошюру под названием De Thiende («десятая»), в которой объявил об универсальном введении десятичной чеканки, мер и весов. быть просто вопросом времени. В современную эпоху многие программы преобразования, например, включенные в калькулятор операционной системы Microsoft Windows 7, отображают составные единицы в сокращенном десятичном формате, а не в расширенном формате (например, отображается «2,5 фута», а не «2 фута 6». в » ).

Третий закон Ньютона

Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.

Словами третий закона Ньютона можно сформулировать так:

Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.

Формула:

\( F_{12} \left( H \right) \) – сила, с которой первое тело действует на второе тело.

\( F_{21} \left( H \right) \) – сила, с которой второе тело отвечает первому.

Пояснить формулу можно с помощью такого рисунка:

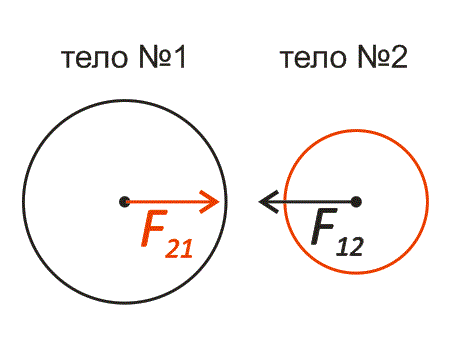Рис. 1. Два шара притягиваются. Сила 12 принадлежит черному шару, а сила 21 – красному

Обратите внимание, что длины красного и черного векторов равны

Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны

Поэтому, формулу третьего закона Ньютона можно записать и так:

Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:

Поэтому, формулу третьего закона Ньютона можно записать и так:

Примечание:

Если перед каким-либо вектором записан знак «минус», то этот вектор развернут в противоположную от выбранной нами сторону.

Между векторами находится знак равенства. Это значит, что длины векторов одинаковые (векторы ).

Разряды чисел

Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:

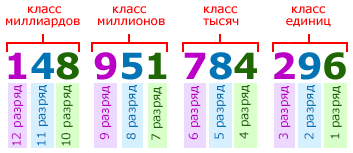
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:

Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
Сотни — единицами третьего разряда и пишутся на третьем месте справа.
Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Пример. Запишите цифрами число, которое содержит:

1) 37 единиц второго класса и 565 единиц первого класса;

2) 450 единиц второго класса и 9 единиц первого класса;

3) 8 единиц второго класса и 50 единиц первого класса.

Решение:

1) 37 565;

2) 450 009;

3) 8 050.

Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:

10 единиц	=	1 десяток;
10 десятков	=	1 сотня;
10 сотен	=	1 тысяча;
10 тысяч	=	1 десяток тысяч;
10 десятков тысяч	=	1 сотня тысяч;
10 сотен тысяч	=	1 тысяча тысяч (1 миллион);

и так далее.

Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.

Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.

Цифра в каком-нибудь разряде означает отсутствие единиц в данном разряде.

Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

24 527 — двадцать четыре тысячи пятьсот двадцать семь.

20 507 — двадцать тысяч пятьсот семь.