Что сначала — сложение или умножение: правила, порядок выполнения действия и рекомендации

Десятичная арифметика

Десятичное представление обычно относится исключительно к письменной системе счисления, в которой арабские цифры используются в качестве цифр для позиционной системы счисления с основанием 10 («десятичная») ; тем не менее, любую систему счисления, основанную на степени 10, например греческие , кириллические , римские или китайские числа, можно концептуально описать как «десятичное представление» или «десятичное представление».

Современные методы для четырех основных операций (сложение, вычитание, умножение и деление) были впервые изобретены Брахмагуптой из Индии. В средневековой Европе это было известно как «Modus Indoram» или метод индейцев. Позиционное обозначение (также известное как «обозначение разряда») относится к представлению или кодированию чисел с использованием одного и того же символа для разных порядков величины (например, «разряды единиц», «разряды десятков», «разряды сотен») и, с точкой счисления , использование тех же символов для представления дробей (например, «десятые доли», «сотые доли»). Например, 507,36 означает 5 сотен (10 2 ), плюс 0 десятков (10 1 ), плюс 7 единиц (10 ), плюс 3 десятых (10 -1 ) плюс 6 сотых (10 -2 ).

Концепция как числа, сравнимого с другими основными цифрами, важна для этого обозначения, как и концепция использования 0 в качестве заполнителя, а также определение умножения и сложения с 0. Использование 0 в качестве заполнителя и Таким образом, использование позиционного обозначения впервые засвидетельствовано в джайнском тексте из Индии под названием Локавибхага , датируемом 458 г. н.э., и только в начале 13 века эти концепции, переданные через научные исследования арабского мира , были введены в Европу по Фибоначчи с использованием индийско-арабской системы счисления.

Алгоризм включает в себя все правила выполнения арифметических вычислений с использованием этого типа письменных чисел. Например, сложение дает сумму двух произвольных чисел. Результат вычисляется путем повторного сложения одиночных цифр из каждого числа, занимающего одну и ту же позицию, начиная справа налево. В таблице сложения с десятью строками и десятью столбцами отображаются все возможные значения для каждой суммы. Если индивидуальная сумма превышает значение 9, результат представляется двумя цифрами. Самая правая цифра — это значение для текущей позиции, а результат последующего сложения цифр слева увеличивается на значение второй (самой левой) цифры, которая всегда равна единице (если не нулю). Эта корректировка называется переносом значения 1.

Процесс умножения двух произвольных чисел аналогичен процессу сложения. В таблице умножения с десятью строками и десятью столбцами перечислены результаты для каждой пары цифр. Если отдельное произведение пары цифр превышает 9, корректировка переноса увеличивает результат любого последующего умножения цифр слева на значение, равное второй (крайней левой) цифре, которая представляет собой любое значение от 1 до 8 ( 9 × 9 = 81 ). Дополнительные шаги определяют конечный результат.

Подобные методы существуют для вычитания и деления.

Создание правильного процесса умножения зависит от отношения между значениями соседних цифр. Значение любой отдельной цифры в цифре зависит от ее положения. Кроме того, каждая позиция слева представляет собой значение, в десять раз превышающее позицию справа. С математической точки зрения, показатель степени для системы счисления (основания) 10 увеличивается на 1 (слева) или уменьшается на 1 (справа). Следовательно, значение любой произвольной цифры умножается на значение формы 10 n с целым числом  n . Список значений, соответствующих всем возможным позициям одной цифры, записывается как {…, 10 2 , 10, 1, 10 −1 , 10 −2 , …}.

Повторное умножение любого значения в этом списке на 10 дает другое значение в списке. В математической терминологии эта характеристика определяется как замыкание , а предыдущий список описывается как закрытый при умножении . Это основа для правильного нахождения результатов умножения с использованием предыдущей техники. Этот результат — один из примеров использования теории чисел .

Арифметические действия

Нахождение по нескольким данным числам одного нового числа называется арифметическим действием. В арифметике рассматривается шесть действий: сложение, вычитание, умножение, деление, возведение в степень, извлечение корня.

1. Сложение. Это действие состоит в том, что по нескольким числам, называемым слагаемыми, находится число, называемое их суммой.

Пример: 4+3=7, где 4 и 3 – слагаемые, а 7 – их сумма.

2. Вычитание – действие, посредством которого по данной сумме (уменьшаемое) и данному слагаемому (вычитаемое) находят искомое слагаемое (разность).
Это действие обратно сложению.

Пример: 7 – 3 = 4, где 7 – уменьшаемое, 3 – вычитаемое, а 4 – разность.

3. Умножение. Умножить некоторое число (множимое) на целое число (множитель) – значит повторить множимое слагаемым столько раз, сколько единиц содержится в множителе. Результат умножения называется произведением.

Пример: 2 ∙ 3 = 6, где 2 – множимое, 3 – множитель, а 6 – произведение. (2 ∙ 3 = 2 + 2+ 2 = 6)

Если множитель и множимое меняются ролями, то произведение остается тем же. Поэтому множитель и множимое также называются сомножителями.

Пример: 2 ∙ 3 = 3 ∙ 2, то есть (2 + 2 + 2 = 3 + 3)

Полагают, что если множителем является 1, то a ∙ 1 = a.

Например: 2 ∙ 1 = 2, 44 ∙ 1 = 44, 13 ∙ 1 = 13.

4. Деление. Посредством деления по данному произведению (делимое) и данному сомножителю (делитель) находят искомый сомножитель (частное). Это действие обратно умножению.

Пример: 8 : 2 = 4, где 8 – делимое, 2 – делитель, а 4 – частное.

Проверка деления: произведение делителя 2 и частного 4 дает делимое 8. 2 ∙ 4 = 8

Деление с остатком

Если при делении целого числа на целое число в частном получается целое число, то такое деление целых чисел называется точным, или, что первое число нацело делится (или просто – делится) на второе.

Например: 35 делится (нацело) на 5, частное есть целое число 7.

Второе число при этом называется делителем первого, первое же – кратным второго.

Во многих случаях можно, не выполняя деления, узнать, делится ли нацело одно целое число на другое (см. признаки делимости).

Точное деление возможно далеко не всегда. В таком случае выполняют так называемое деление с остатком. В этом случае находят такое наибольшее число, которое при умножении на делитель даст произведение, не превосходящее делимого. Это число называется неполным частным. Разность между делимым и произведением делителя на неполное частное называется остатком от деления.
Делимое равно делителю, умноженное на неполное частное, плюс остаток. Остаток всегда меньше делителя.

Пример:
Неполное частное от деления числа 27 на 4 равно 6, а остаток равен 3. Очевидно, 27 = 4∙6 + 3 и 3˂4.

5. Возведение в степень. Возвести некоторое число в целую степень (во вторую, в третью и т.д.) – значит взять это число сомножителем два, три раза и т.д. Иначе говоря, возведение в степень выполняется повторным умножением.
Число, которое берётся сомножителем, называется основанием степени; число, показывающее, сколько раз повторяется основание, называется показателем степени; результат возведения числа в степень называется степенью этого числа.

Пример: 2∙2∙2 = 2³ = 8; где 2 – основание степени, 3 – показатель степени, 8 – степень.

Вторую степень числа иначе называют квадратом, третью степень – кубом. Первой степенью числа называют само это число.

6. Извлечение корня есть действие, посредством которого по данной степени (подкоренное число) и данному показателю степени (показатель корня) находят искомое основание (корень). Это действие обратно возведению в степень.

Пример: ³√64 = 4; где 64 – подкоренное число, 3 – показатель корня, 4 – корень.

Проверка извлечения корня: 4³=64. Возведение числа 4 в 3-ю степень даёт 64.

Корень второй степени иначе называют квадратным; корень третьей степени – кубическим.
При знаке квадратного корня показатель корня принято опускать: √36 = 6 означает ²√36 = 6.

Использованная лит-ра:Справочник по элементарной математике — Выгодский М.Я., «Наука», 1974 г.
Справочник по математике. Пособие для учащихся 9—11 кл. — Шахно К. У., «Учпедгиз», 1961 г.

→ Читайте по теме: Признаки делимости

→ Арифметика

→ В раздел Советы

При полной или частичной публикации статьи в

Интернете обязательно указание активной гиперссылки на источник

http://programmistan.narod.ru

Операция сдвига по разрядной сетке

В
компьютерах, кроме операции алгебраического
суммирования двоичных чисел, к которой
относятся операции сложения и вычитания,
выполняется операция
сдвига числа по
разрядной сетке влево и вправо,
осуществляющая, фактически, умножение
и деление двоичных чисел.

В
случае сдвига влево осуществляется
умножение двоичного числа на 2j,
а при
сдвиге вправо –
деление на 2j,
где j
– количество разрядов, на которое
сдвигается двоичное число.

Например,
осуществить сдвиг на 2 разряда

1)
000011₂
= 3₁₀
влево

001100₂
= 12₁₀

т.
е. 3 х 4(22)
= 12₁₀

2)
001000₂
= 8₁₀
вправо

000010₂
= 2₁₀

т.
е. 8 : 4(22)
= 2₁₀

В
компьютерах часто используется
циклический
сдвиг,
при выполнении которого разрядная
сетка, отведенная для операнда
(числа, над которым производится
действие), представляется замкнутой в
кольцо. Тогда при
сдвиге влево
содержимое старшего разряда попадает
в младший разряд операнда, а при
сдвиге вправо
содержимое младшего разряда попадает
в старший разряд операнда.

Решение задач

Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.

Как решаем: перемножим делимое и натуральное число.

Ответ: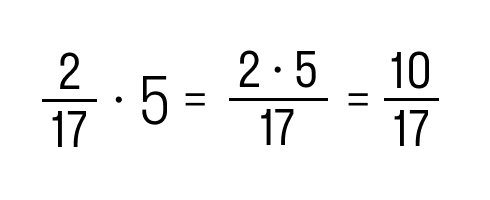 

Задание 2. Выполнить умножение 4/15 и 55/6.

Как решаем:

перемножим числители между собой и знаменатели соответственно

сократим полученное

выделим целую часть

Ответ: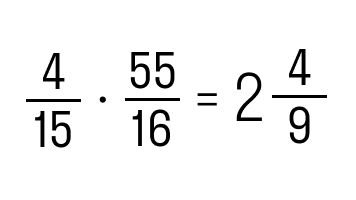

Задание 3. Выполнить умножение одной целой трех седьмых на шесть.

Как решаем:

• переводим смешанное число в неправильную дробь,
• умножаем делимое на натуральное число,
• сократим полученное,
• преобразуем в смешанное число.

Ответ: 

Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:

• Раз 
• Два
• Три

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Наши преподаватели понятно объяснят что угодно — от дробей до синусов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем.

Порядок выполнения действий в математике. Правила и примеры.

Рубрики Алгебра

Определение: Порядок выполнения арифметических действий в выражении — это последовательность проводимых вычислений в данном выражении.

Порядок выполнения действий один и для числовых выражений, и для буквенных выражений. Действиями первой ступени являются сложение и вычитание. Действиями второй ступени являются умножение и деление.

 Последовательность выполнения арифметических операций в числовом выражении следующая:

•  произвести вычисления в скобках или раскрыть скобки в выражении (если они есть);
•  выполнить все действия второй ступени (умножение и деление);
•  выполнить действия первой ступени (сложение и вычитание).

Таков порядок выполнения арифметических действий в математике. Давайте посмотрим, как эти правила выглядели в начале 20 века и изучим примеры из учебника А.П Киселева по алгебре.

Правила выполнения математических действий

Относительно порядка, в котором надо производить действия, указанные в алгебраическом выражении, условились: сначала производить действия высшего порядка, т. е. возведение к степень и извлечение корня, затем умножение и деление и, наконец, сложение и вычитание.
Так, если написано выражение: 3a²*b-b³/c +d, то при вычислении его надо сначала произвести возведение в степень (число а возвести в квадрат и число b в куб), затем умножение и деление

1. 3 умножить на а² и полученный результат умножить на b
2. b³ разделить на с
3. наконец, вычитание и сложение (из 3a²b вычесть b³ /c и к результату прибавить d).

Порядок выполнения действий со скобками

Когда приходится по условиям задачи отступать от этого порядка действий, то употребляются скобки. Скобки показывают, что действия над числами, заключёнными в скобки, надо произвести ранее других. Например, выражения:

5+7*2 и (5+7)*2
означают не одно и то же. В первом случае нужно 7 умножить на 2 и результат прибавить к 5 (получаем 19). Во втором случае надо сначала сложить 5 и 7 и результат умножить на 2 (получаем 24).
Точно так же, если написано:

(а + b)с — d,
то это значит, что сначала надо сложить а и b, затем полученное число умножить на с и из того, что получится, вычесть d.
Когда приходится заключать в скобки такое выражение, в котором есть свои скобки, то новым скобкам придают какую-
нибудь другую форму. Например выражение:a{b-}
означает, что из d вычитается е, полученная разность складывается с с, полученная сумма вычитается из b и на эту разность умножается а.
Скобкам дают обыкновенно такие названия: круглые скобки (), квадратные, или ломаные, скобки , фигурные скобки { }.
Когда в выражение входят несколько скобок, то обычно сначала производят действия над числами, заключёнными в круглые скобки, затем над числами в квадратных скобках и, наконец, в фигурных. Производя указанные в скобках действия, мы уничтожаем, или, как говорят, раскрываем скобки. Так, в выражении:5 • {24 — 2 • }
сначала раскрываем круглые скобки:5-{24-2*}.
Затем раскрываем квадратные скобки: 5 • {24 — 2*9}.
Наконец, раскрываем фигурные скобки: 5 • 6 = 30.

Тренажеры:

Друг Доктор

Ментальная арифметика (быстрый счёт) онлайн — тренажёр и теория.

Настоящий курс ментальной арифметики (быстрого счёта) основан на наиболее эффективных приёмах быстрого счета, разработанных профессиональными математиками.

Если вы хотите научиться выполнять арифметические операции исключительно в уме с поразительной скоростью, а также овладеть математическими трюками, которые дадут вам преимущества в повседневной жизни и удивят ваших друзей, то этот курс для вас.

В отличие от активно рекламируемых платных курсов ментальной арифметики с использованием абакуса, предлагаемая методика подразумевает творческий подход к изучению приёмов быстрого счёта, что ведёт к развитию мышления и памяти.

Каждый из уроков курса состоит из теоретической части и практических занятий на онлайн-тренажёре.

Данный курс ментальной арифметики подходит как для взрослых, так и для детей.

Клуб Ментальной арифметики

Основные возможности тренажера

• Автоматическая генерация примеров на основе заданных параметров
• Сложение, вычитание, умножение, деление
• Любое сочетание законов на 5 или 10
• Произвольное количество разрядов для чисел
• Десятичные дроби для умножения и деления
• Показ числе на счетах для начинающих
• Возможность настройки временных интервалов
• Индивидуальный и групповой режим
• Показ примеров на случайном месте экрана, изменение шрифта и цвета
• Расчет времени окончания всего теста
• Озвучивание цифр и подсказок
• Распознавание ответов с помощью микрофона. Возможность управлять процессом исключительно голосом
• Работа на мобильных устройствах
• Сохранение настроек в браузере

Легкие числа

Бесплатный месяц обучения ментальной арифметике

• доступ к обучению на срок 1 месяц
• пошаговые задания на каждый день
• текстовые и видео уроки
• полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан
• консультации по e-mail

Полный доступ к игре на 1 месяц (3 USD)

• доступ к обучению на срок 1 месяц
• полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан

Обучение ментальной арифметике 1 месяц (5 USD)

• доступ к обучению на срок 1 месяц
• пошаговые задания на каждый день
• текстовые и видео уроки
• полный доступ к тренажеру для обучения ментальной арифметике с помощью счет абакус/соробан
• консультации по e-mail

Соробан77.ру

«Тренировочный режим» онлайн-тренажера предназначен для практического закрепления знаний по полному курсу теории «Соробан», т.е. рассчитан на пользователя, успешно освоившего все восемь уровней. Порядок пользования онлайн-тренажером приведен ниже:

1. В окне онлайн-тренажера необходимо ввести исходные данные для работы
2. В поле ввода «КОЛИЧЕСТВО ЧИСЕЛ» вводится любое целое число от «3» до «99», которое определяет желаемое количество последовательно выводимых на экран чисел.
3. В поле ввода «ЗАДЕРЖКА» вводится любое целое число от «1» до «30 000», которое определяет интервал времени между выводом на экран предыдущего и последующего значений, выраженный в миллисекундах.
4. В поле ввода «ОТ» вводится значение минимального разряда выводимых чисел (от «1-значные» до «5-значные») путем выбора одного из значений в выпадающей вкладке.
5. В поле ввода «ДО» вводится значение максимального разряда выводимых чисел (от «1-значные» до «5-значные») путем выбора одного из значений в выпадающей вкладке.

Угадайка

Представляем вам интерактивный обучающий сайт, с элементами которого можно взаимодействовать, для изучения арифметики с помощью абакуса (соробана). Абакус — это отличный инструмент, чтобы научиться быстрому счету и особенно может быть полезен для школьников младших классов. Идея заключается в том, чтобы отойти от «скучных» и «сухих» цифр и перейти к «образному счету». С помощью бусинок абакуса у человека возникают образы для каждого математического действия.

Образы намного лучше запоминаются, чем просто цифры и математические знаки.

Человеческий мозг работает с образами в разы быстрее чем с простым счетом «на пальцах».

Последовательно выполняя одно задание за другим, вы сможете освоить принцип счета на абакус и помочь вашему ребенку сориентироваться, как считать на абакусе (соробане).

Дроби на английском языке

Простые дроби – common fractions

Если у вас с математикой так же “прекрасно”, как у меня, напомню самое основное о дробях.

Простые дроби (common fractions) состоят из числителя (numerator) и знаменателя (denominator). Напоминаю, числитель сверху, знаменатель снизу Если число состоит из целого и дроби, например 1½, – это называется смешанная дробь или смешанное число (mixed numeral).

Числитель выражается количественным числительным, а знаменатель порядковым. Наиболее употребительные в речи дроби 1/2, 1/3, 1/4 в русском языке имеют не только “умные” называния “одна вторая”, “одна третья”, одна четвертая, но и простые: половина, треть, четверть. В английском точно так же.

• 1/2 – a half, one half.
• 1/3 – a third, one third.
• 1/4 – a quarter, one fourth.
• 1/5 – one fifth.
• 1/6 – one sixth.
• 2/3 – two thirds.
• 3/4 – three fourths.
• 1/8 – one eighth.
• 1/10 – a tenth.
• 1/100 – a hundredth.
• 1¼ – one and a quarter.
• 1½ – one and a half.
• 1¾ – one and three quarters.

Обратите внимание, когда числитель больше одного, к окончанию добавляется -s, так как знаменатель используется во множественном числе (как и в русском: две третьих, три четвертых). Существительное, которое определяется дробью, используется с предлогом of:

Существительное, которое определяется дробью, используется с предлогом of:

• 3/4 mile – Three fourths of a mile.
• 1/4 bottle – A quarter of a bottle.

Существительное, определяемое смешанной дробью, используется без предлога, но во множественном числе:

• 2 ½ miles – Two and a half miles.
• 1¼ bottles – One and a quarter bottles.

Десятичные дроби – decimal fractions, decimals

В английском в десятичных дробях (decimals) целое от дроби отделяется точкой (point), а не запятой, как у нас.

Ноль перед точкой называется zero или (британский вариант) nought. Ноль после точки может называться oh (как буква “o”), zero, nought. Лично я для простоты всегда говорю zero, потому что это слово проще выговорить и расслышать. Если целое число в дроби равно нулю, его часто опускают в речи, начиная говорить сразу с “point”.

Целое число читается как обычное количественное числительное, например 45.1 – forty five point one. Но в дробной части каждая цифра читается отдельно тоже как количественное: 2.45 – two point four five (а не two point forty five).

Примеры:

• 0.1 – Point one, zero point one.
• 0.35 – Point three five, zero point three five.
• 1.25 – One point two five.
• 35.158 – Thirty five point one five eight.
• 15.05 – Fifteen point zero five.

Смешанные числа

Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:

Записать неправильную дробь: 79/11.
Рассчитать целое число: 79/11=7.
Вычислить новое значение числителя: 79−11*7=2.
Записать смешанную величину: 7 2/11.

Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:

Записать смешанное выражение: 7[2/11].
Вычислить величину нового числителя: 7*11+2=79.
Результат: 79/11.

Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.

Некоторые правила, которые необходимо соблюдать при решении примеров без скобок:

• Если в задании необходимо выполнить ряд действий, нужно сначала выполнить деление или умножение, затем сложение. Все действия выполняются по ходу письма. В противном случае, результат решения будет не верным.

• Если в примере требуется выполнить сложение и вычитание, выполняем по порядку, слева направо.

27-5+15=37 (при решении примера руководствуемся правилом. Сначала выполняем вычитание, затем – сложение).

• Научите ребёнка всегда планировать и нумеровать выполняемые действия.

• Ответы на каждое решённое действие записываются над примером. Так ребёнку гораздо легче будет ориентироваться в действиях.

Рассмотрим ещё один вариант, где необходимо распределить действия по порядку:

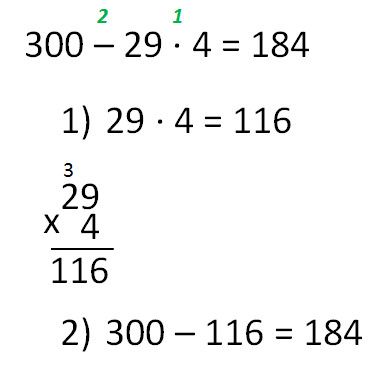
Как видим, при решении соблюдено правило, сначала ищем произведение, после — разность.

Это простые примеры, при решении которых, необходима внимательность. Многие дети впадают в ступор при виде задания, в котором присутствует не только умножение и деление, но и скобки. У школьника, не знающего порядок выполнения действий, возникают вопросы, которые мешают выполнить задание.

Как говорилось в правиле, сначала найдём произведение или частное, а потом всё остальное. Но тут же есть скобки! Как поступить в этом случае?

Решение примеров со скобками

Разберём конкретный пример:

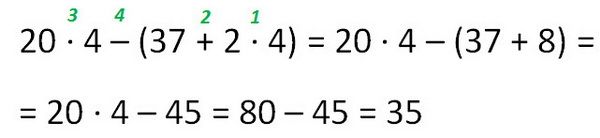
• При выполнении данного задания, сначала найдём значение выражения, заключённого в скобки.
• Начать следует с умножения, далее – сложение.
• После того, как выражение в скобках решено, приступаем к действиям вне их.
• По правилам порядка действий, следующим шагом будет умножение.
• Завершающим этапом станет вычитание.

Как видим на наглядном примере, все действия пронумерованы. Для закрепления темы предложите ребёнку решить самостоятельно несколько примеров:

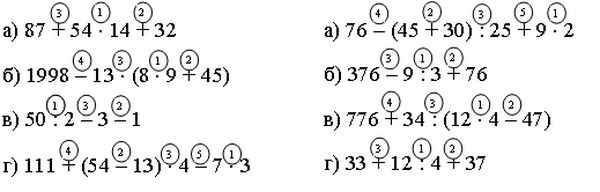
Порядок, по которому следует вычислять значение выражения уже расставлен. Ребёнку останется только выполнить непосредственно решение.

Усложним задачу. Пусть ребёнок найдёт значение выражений самостоятельно.

7*3-5*4+(20-19) 14+2*3-(13-9) 17+2*5+(28-2) 5*3+15-(2-1*2) 24-3*2-(56-4*3) 14+12-3*(21-7)

Приучите ребёнка решать все задания в черновом варианте. В таком случае, у школьника будет возможность исправить не верное решение или помарки. В рабочей тетради исправления не допустимы. Выполняя самостоятельно задания, дети видят свои ошибки.

Родители, в свою очередь, должны обратить внимание на ошибки, помочь ребёнку разобраться и исправить их. Не стоит нагружать мозг школьника большими объёмами заданий

Такими действиями вы отобьёте стремление ребёнка к знаниям. Во всём должно быть чувство меры.

Делайте перерыв. Ребёнок должен отвлекаться и отдыхать от занятий. Главное помнить, что не все обладают математическим складом ума. Может из вашего ребёнка вырастет знаменитый философ.