Что это — истинное высказывание

Логика высказываний: определение и применение

Логика высказываний, называемая также пропозициональной логикой — раздел математики
и логики, изучающий логические формы сложных высказываний, построенных из простых или элементарных
высказываний с помощью логических операций.

Высказываниями принято считать такие
предложения (написанные на «словесном» либо математическом языке),
о которых можно сказать одно из двух: либо они являются истинными, либо ложными.

С математическими высказываний проще всего: они всегда имеют либо значение
«истина», либо значение «ложь». Для высказываний, сделанных на «словесном» языке, понятия «истинности» и «ложности»
несколько более расплывчаты. Однако, например, такие словесные формы, как «Иди домой» и «Идёт ли дождь?»,
не являются высказываниями. Поэтому понятно, что высказываниями являются такие словесные формы, в которых
что-либо утверждается. Не являются высказываниями вопросительные или восклицательные предложения,
обращения, а также пожелания или требования. Их невозможно оценить значениями «истина» и «ложь».

Логика высказываний отвлекается от содержательной нагрузки высказываний и изучает их
истинностное значение, то есть является ли высказывание истинным или ложным.

Рисунок слева — иллюстрация явления, известного как «Парадокс лжеца». При этом,
на взгляд автора проекта, такие парадоксы возможны только в средах, несвободных от политических заморочек,
где на ком-то могут априори поставить клеймо лжеца. В естественном многослойном мире на предмет «истины»
или «лжи» оцениваются только отдельно взятые высказывания. И далее на этом уроке вам представится
возможность самим оценить на этот предмет немало высказываний (а затем посмотреть правильные ответы). В том числе сложных высказываний, в
которых более простые связаны между собой знаками логических операций. Но прежде рассмотрим сами эти
операции над высказываниями.

17.Операции алгебры логики. Таблицы истинности логических операций. Вычисление логических выражений.

Сложное логическое высказывание
строится из простых с помощью логических
связок (таких как «И», «ИЛИ»,
«НЕ»), которые называютсялогическими
операциями.

• На улице светит солнце и на улице
  идет дождь. (А и В)

• На улице светит солнце или на улице
  идет дождь. (А или В)

Основные
логические операции:

• НЕ(логическое отрицание,инверсия)

• ИЛИ(логическое сложение,дизъюнкция)

• И(логическое умножение,конъюнкция)

Операция НЕ
(отрицание, инверсия)

Отрицание (инверсия) – операция
логического отрицания.

Добавляется частица НЕили словаНЕВЕРНО, ЧТО…

Обозначение: не, not, ¬ ,
¯.

Если исходное выражение истинно, то
результат его отрицания будет
ложным, и наоборот, если исходное
выражение ложно, то оно будет истинным.

А – Земля вращается вокруг
Солнца – истинно

¬А – Земля не вращается
вокруг Солнца – ложно

Операция И
(логическое умножение, конъюнкция)

Конъюнкция (логическое умножение)
– соединение двух логических выражений
(высказываний) с помощью союзаИ.

Обозначение: и, and, ×, &
,Ù

Логическая операция конъюнкция
истинна только в том случае, если оба
простых высказывания истинны, в противном
случае она ложна.

А – У меня есть знания для
сдачи зачета.

В – У меня есть желание для
сдачи зачета.

У меня есть знания И желание для сдачи
зачета.

AÙB

Операция ИЛИ
(логическое сложение, дизъюнкция)

Дизъюнкция (логическое сложение) –
соединение двух логических высказываний
с помощью союза ИЛИ.

Обозначение: или, or, +,V

Логическая операция дизъюнкция ложна,
если оба простых высказывания ложны.
В остальных случаях она истинна.

A – Летом я поеду в лагерь

B – Летом я поеду к бабушке

Летом я поеду в лагерь или поеду к
бабушке

AVB

Другие логические
операции:

Импликация
(«если …, то …»)

Импликация (логическое следование)– связывает два логических выражения,
из которых первое является условием,
а второе – следствием из этого условия.
Операция обозначается словами: «Если…,
то…» (Если А, то В).

Результат операции импликацииложен только тогда, когда предпосылка
А истинна, а заключение В (следствие)
ложно.

А – идёт дождь

В – на улице сыро

Если идёт дождь, то на улице сыро.

А → В

Эквивалентность
(«тогда и только тогда, …»)

Эквивалентность (логическое
тождество, равнозначность) –
определяет результат сравнения двух
логических выражений. Операция
обозначается словами: «…тогда и только
тогда, когда…» (А т. и т. т. когда В)

Обозначение: «,Û,º, ~

Результат операции эквивалентностьистинен только тогда, когда А и В
одновременно истинны или одновременно
ложны.

А – день сменяет ночь

В – солнце скрывается за горизонтом

День сменяет ночь тогда и только тогда,
когда солнце скрывается за горизонтом.

А ~ В

Таблицы
истинности:

Таблица истинности отрицания (Операция
НЕ (отрицание, инверсия):

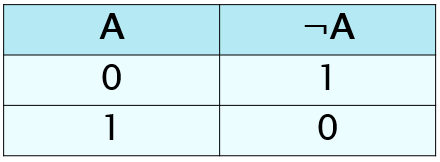
Таблица истинности конъюнкции (Операция
И (логическое умножение, конъюнкция):

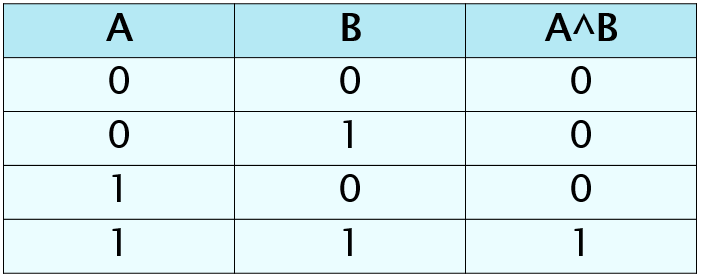
Таблица истинности дизъюнкции (Операция
ИЛИ (логическое сложение, дизъюнкция):

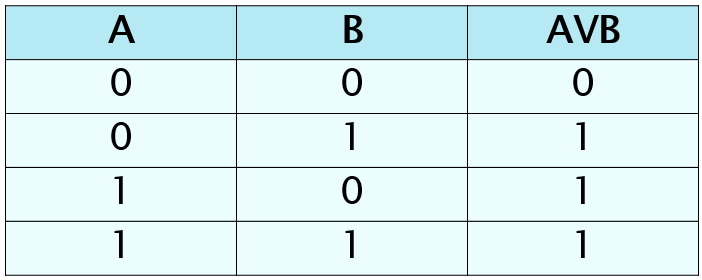
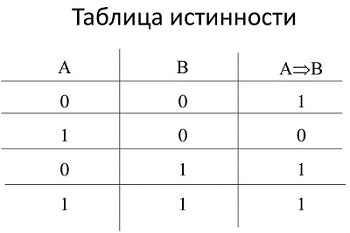
Таблица истинности импликации(Импликация
(«если …, то …»):

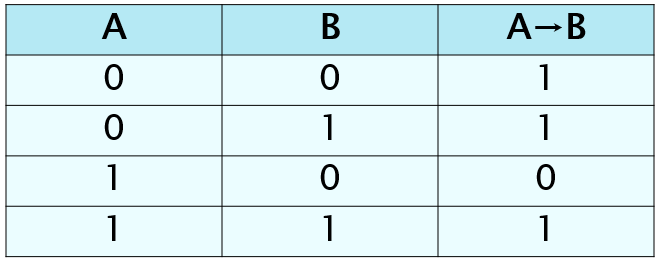
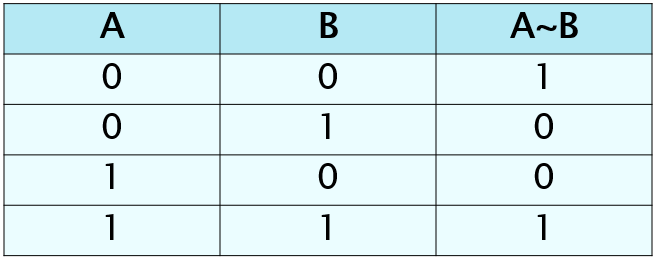
Таблица истинности эквивалентности
(Эквивалентность («тогда и только тогда,
…»):

Примечания

1. ↑ , с. 264—266, 534—536.
2. , с. 67.
3. Стяжкин Н. И.  Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
4. , с. 30.
5. Пратт Т.  Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
6. Грогоно П.  Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
7. Вегнер П.  Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
8. Эллис М., Строуструп Б.  Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
9. Яблонский С. В.  Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
10. Рвачёв В. Л.  Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
11. ↑ Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Тавтологии и противоречия

Логические тавтологии (или просто тавтологии) — это такие формулы логики высказываний,
что если буквы произвольным образом заменить высказываниями
(истинными или ложными), то в результате всегда получится истинное высказывание.

Так как истинность или ложность сложных высказываний зависит лишь от значений, а не
от содержания высказываний, каждому из которых соответствует определённая буква, то проверку того,
является ли данное высказывание тавтологией, можно подставить следующим способом. В исследуемом
выражении на место букв подставляются значения 1 и 0 (соответственно «истина» и «ложь») всеми возможными
способами и с использованием логических операций вычисляются логические значения выражений. Если все
эти значения равны 1, то исследуемое выражение есть тавтология, а если хотя бы одна подстановка даёт 0,
то это не тавтология.

Таким образом, формула логики высказываний, которая принимает значение «истина» при
любом распределении значений входящих в эту формулу атомов, называется тождественно истинной формулой
или тавтологией.

Противоположный смысл имеет логическое противоречие. Если все значения высказываний равны
0, то выражение есть логическое противоречие.

Таким образом, формула логики высказываний, которая принимает значение «ложь» при
любом распределении значений входящих в эту формулу атомов, называется тождественно ложной формулой
или противоречием.

Кроме тавтологий и логических противоречий существуют такие формулы логики высказываний,
которые не являются ни тавтологиями, ни противоречиями.

Пример 9. Составьте таблицу истинности для формулы логики высказываний
и определите, является ли
она тавтологией, противоречием или ни тем, ни другим.

Решение. Составляем таблицу истинности:

И	И	И	И	И
И	Л	Л	Л	И
Л	И	Л	И	И
Л	Л	Л	Л	И

В значениях импликации не встречаем строку, в которой из «истины» следует «ложь». Все
значения исходного высказывания равны «истине». Следовательно, данная формула логики высказываний является тавтологией.

Пример 10. Составьте таблицу истинности для формулы логики высказываний
и определите, является ли
она тавтологией, противоречием или ни тем, ни другим.

Решение. Составляем таблицу истинности:

И	И	И	И	И	И
И	И	Л	И	Л	Л
И	Л	И	Л	И	И
И	Л	Л	Л	Л	И
Л	И	И	Л	И	И
Л	И	Л	Л	Л	И
Л	Л	И	Л	И	И
Л	Л	Л	Л	Л	И

Среди значений данного высказывания одно — «ложь», остальные — «истина». Следовательно, данная формула логики высказываний не является ни тавтологией, ни
противоречием.

Виды предложений по цели высказывания

Цель высказывания — это цель, с которой предложение произносится или пишется. Целью высказывания может быть сообщение, вопрос или просьба (приказ, побуждение к действию, совет).

Предложения с точки зрения выраженного в них содержания, то есть по цели высказывания, бывают повествовательные, вопросительные и побудительные.

• Повествовательное предложение — это предложение, в котором что-либо сообщается, что-либо утверждается или что-либо отрицается:

  На улице плохая погода.

  Дельфин – млекопитающее.

  Дельфин – не рыба.

  В конце повествовательного предложения ставится точка, восклицательный знак или многоточие:

  Нам пора домой.

  Мы идём в кино!

  А вот и рассвет…

  Повествовательные предложения произносятся с повествовательной интонацией — повышение голоса на одном из членов предложения и понижение его к концу предложения.

• Вопросительное предложение — это предложение, которое содержит вопрос. В конце вопросительного предложения ставится вопросительный знак:

  Что ты делаешь?

  Вопросительное предложение может содержать вопросительные слова:

  Какой это цвет?

  Где ты сегодня был?

  Иногда вопрос выражается с помощью вопросительных частиц  ли, ль, разве  и др.:

  Не хочешь ли тоже поехать?

  Тебе ль не знать?

  Разве тебе уже можно?

  Вопрос может выражаться только вопросительной интонацией, в этом случае вопросительных слов и частиц предложение содержать не будет. Повышение голоса будет падать на главное по смыслу слово в предложении:

  Поедешь с нами на дачу?

  Вы Иванова ждёте?

  Вопросительные предложения произносятся с вопросительной интонацией — повышение тона голоса на слове, с которым связан смысл вопроса, и к концу предложения:

  Вам нравится читать?

  Вам нравится читать?

  Вам нравится читать?

• Побудительное предложение — это предложение, которое содержит повеление, просьбу или запрет. В конце повелительного предложения, в зависимости от того, произносится оно спокойным или повышенным тоном, ставится точка или восклицательный знак:

  Закройте дверь.

  Не входить!

  Побудительные предложения часто содержат обращения:

  Оля, закрой окно.

  Примечание: побудительные предложения часто имеют только один главный член — сказуемое, выраженное глаголом в повелительном наклонении:

  Не ходите по мокрому полу.

  Побудительные предложения произносятся с побудительной интонацией — с повышением голоса, напряжённо.

1.6. Дедуктивні висновки у логіці висловлювань

У логіці висловлювань правила висновку використовують, щоб виводити одні істинні речення з інших істинних речень. У коректному дедуктивному виведенні висновок з необхідністю випливає з посилок.

Означення 1.6.1. Логічним наслідком висловлювання є висловлювання 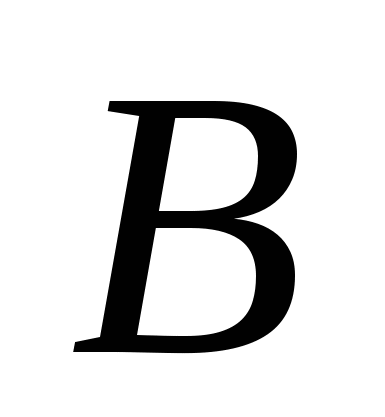, якщо формула є тотожно істинною. Це визначення може бути узагальнено для випадку висловлювань, якщо – тотожно істинна формула.

Приклад 1.6.1. Показати, що висловлювання 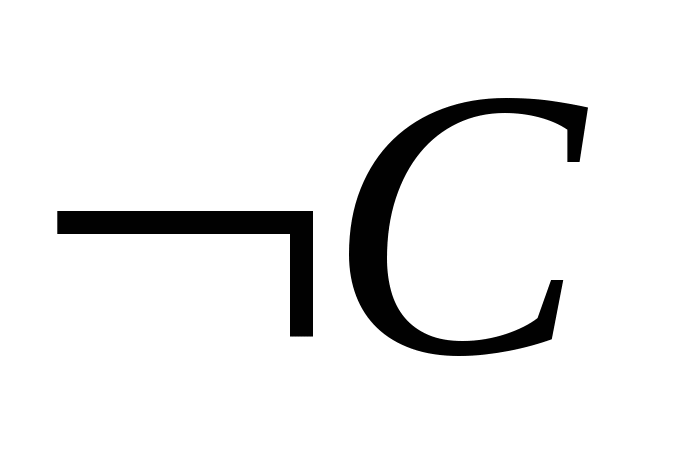є логічним наслідком висловлювання A\wedge  \urcorner C.

Розв’язання. Доведемо, що формула  A\wedge \urcorner C((A\wedge B)\vee \urcorner C) є загальнозначущою. Для її доведення використаємо тотожності логіки висловлювань та еквівалентні перетворення

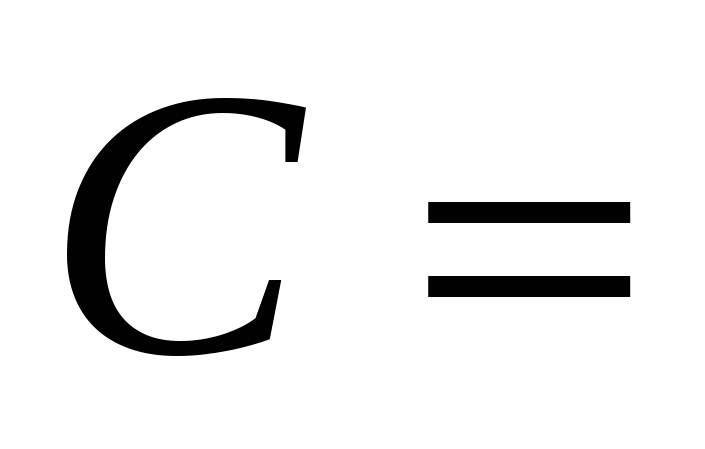
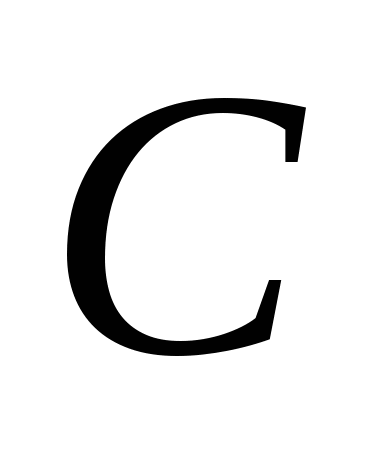
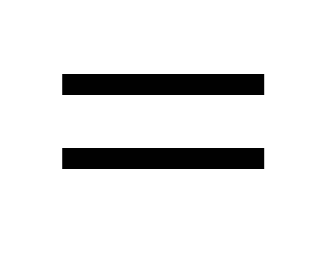II.

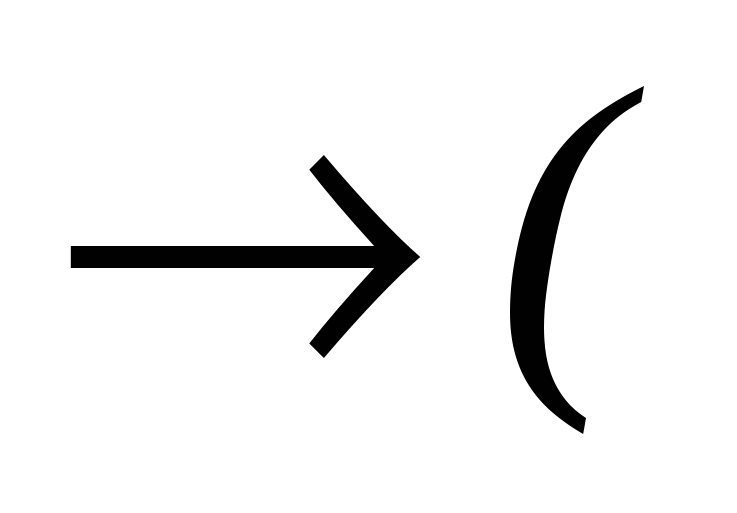
Отже формула 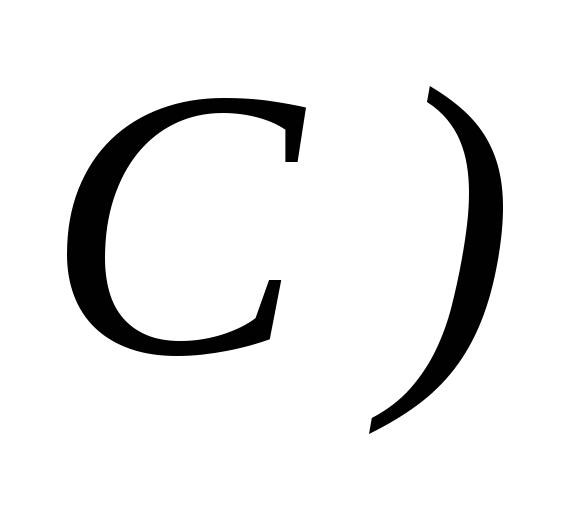є загальнозначущою, а за означенням 1.6.1 — логічний наслідок.

Означення 1.6.1. Дедуктивним висловлюванням називають висновок формули з формули , заснований на тому, що є логічним наслідком .

Приклад 1.6.2. Довести правильність міркування за дедукцією — “ Постанова кабинету Міністрів ухвалюється, якщо за неї голосує більшість міністрів. За постанову не проголосувала більшість міністрів, тому постанова не ухвалюється ”.

Розв’язання.До речень висловлювання введемо такі атоми :

A – “ за постанову проголосувала більшість міністрів ”;

B – “ постанова ухвалюється ”; A – “ за постанову не проголосувала більшість міністрів ”; B – “ постанова не ухвалюється ”;

Тоді засновки і висновки зазначимо відповідно через ~, , і приєднавши за допомогою імплікації до кон’юнкції засновків ~ висновок одержимо ~.

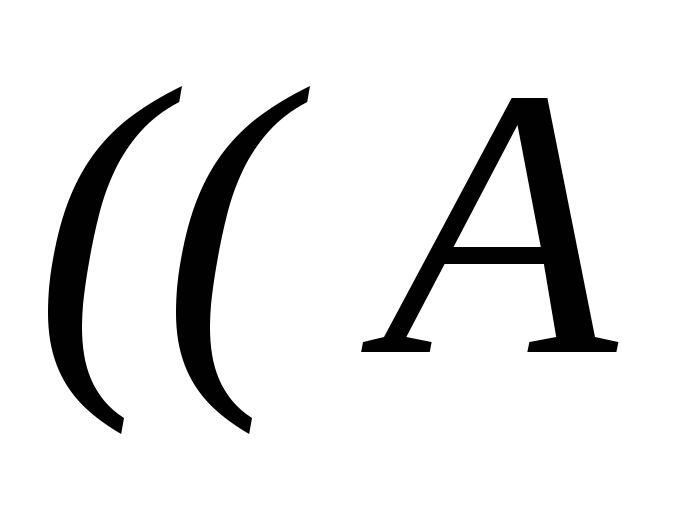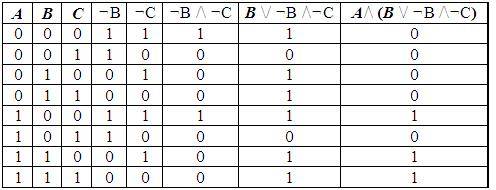
Перевіримо за допомогою таблиці істинності, табл. 1.6.1., що задана імплікація ~ є логічним наслідком.

Таблиця 1.6.1

		~			~	~
X	X	I	I	I	I	I
X	I	X	I	X	X	I
I	X	X	X	I	X	I
I	I	I	X	X	X	I

Із таблиці істинності слідує, що отримано тотожно істинне висловлювання. Отже, виходячи із законів, задане по умові міркування задовольняє визначення дедуктивного висновку. Таким чином, істинність висновку в дедуктивному висновку гарантується істинністю засновків.

Твердження 1.6.1. Висловлювання є логічним наслідком висловлювання , якщо висловлювання є тотожно хибним.

Твердження 1.6.2. Висловлювання є логічним наслідком висловлювання , якщо на всіх інтерпретаціях, на яких істинне, теж істинне.

Тотожна істинність або хибність засновків імплікації дозволяє зробити висновок про істинність або хибність наслідку.

Твердження 1.6.3 Якщо висловлювання є логічним наслідком висловлювання , а висловлювання – тотожно істинне висловлювання, то висловлювання також – тотожно істинне.

Твердження 1.6.4 Якщо висловлювання є тотожно хибним, то для будь-якого висловлювання правильно, що .

Правила для дедуктивного висновку будують на підставі загальнозначущих формул логіки висловлень виду .

Для наочного зображення правила умовиводів схематично записують за допомогою риски, над якою пишуть посилки, а під нею – висновок. Якщо посилок дві й більше, їх записують одну під одною ( табл. 1.6.2.)

Таблиця 1.6.2

Правило дедукти  вного висновку	Тавтологія	Назва правила
A_____________		Правило відділення (Modus Ponens)
B→C \overline{A\rightarrow C}		Гіпотетичний силогізм
______________		Від’ємна форма правила відділення (Modus Tollens)
________________		Правило введення диз’юнції (правило розширення)
_______________		Правило введення кон’юнції
____________		Правило видалення диз’юнції (диз’юнктивний силогізм)
____________		Правило видалення кон’юнції
_____________		Правило контрапозиції імплікації
______________		Правило вибору
		Правило виключаючого вибору
		Правило зведення до абсурду (Reduction ad Absurdum)

Правильність всіх перелічених в табл. 1.6.2 логічних висловлювань можна довести за допомогою таблиць істинності. З усіх правил, наведених в табл. 1.6.2, найбільш часто використовується правило відділення. Правило відділення має такий логічний сенс, якщо засновок правильний, то правильний і наслідок із нього.

Приклад 1.6.3. Дано висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ”. Також відомо, що “n ділиться на 9”. Який висновок можна зробити, виходячи з ціх двох висловлювань?

Розв’язання. Введемо атомарні висловлювання

A – “ n ділиться на 9 ”,

B – “ n ділиться на 3 ”.

Висловлювання “ Якщо n ділиться на 9, то n ділиться на 3 ” можна записати у вигляді формули . З одночасного виконання засновків і можна зробити висновок за правилом відділення “ n ділиться на 3”.

Алгебра высказываний

Высказывание – повествовательное предложение, о котором можно сказать истинно оно или ложно. В алгебре простым высказываниям ставятся в соответствии логические переменные (А, В, С и т.д.)

Логическая переменная – это простое высказывание. Логические переменные обозначаются прописными и строчными латинскими буквами (a-z, A-Z) и могут принимать всего два значения – 1, если высказывание истинно, или 0, если высказывание ложно.

 Пример высказываний:

 
 
 
 
 
 
 
 

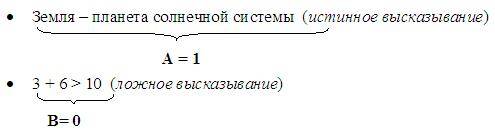
Логическая функция – это сложное высказывание, которое получается в результате проведения логических операций над простыми высказываниями.

Для образования сложных высказываний наиболее часто используются базовые логические операции, выражаемые с помощью логических связок «и», «или», «не».Например,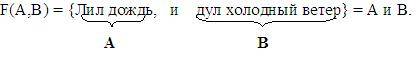

Многие люди  не любят сырую погоду.

Пусть А = «Многие люди любят сырую погоду». Получаем логическую функцию F(A) = не А.

Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.

Логическая формула (логическое выражение) — формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является ИСТИНА (1) или ЛОЖЬ (0).

Значение логической функции зависит от значений входящих в нее логических переменных. Поэтому значение логической функции можно определить с помощью специальной таблицы (таблицы истинности), в которой перечислены все возможные значения входящих логических переменных и соответствующие им значения функции.

                                                                      Основные (базовые) логические операции:

1. Логическое умножение (конъюнкция), от лат. konjunctio – связываю:•    Объединение двух (или нескольких) высказываний в одно с помощью союза И;•     в языках программирования — And. •    Принятые обозначения: /\ , •, и, and.•    В алгебре множеств конъюнкции соответствует операция пересечения множеств.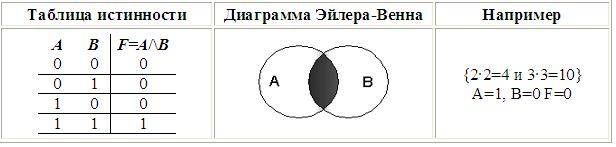  

Конъюнкция истинна тогда и только тогда, все, входящие в нее высказывания истинны.

Пример: Рассмотрим составное высказывание  «2 • 2 = 4 и 3 • 3 = 10». Выделим простые высказывания:А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)В = «3 • 3 = 10» = 0 (т.к. это ложное высказывание)Поэтому, логическая функция F(A, B) = A /\ B = 1 /\ 0 = 0 (в соответствии с таблицей истинности), то есть данное составное высказывание ложное.

2. Логическое сложение (дизъюнкция), от лат. disjunctio – различаю:•    Объединение двух (или нескольких) высказываний в одно с помощью союза ИЛИ;•     в языках программирования — Or. •    Обозначение:  \/, +, или, or.•    В алгебре множеств дизъюнкции соответствует операция объединения множеств.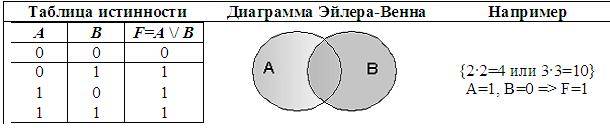  

Дизъюнкция ложна тогда и только тогда, все, входящие в нее высказывания ложны.

Пример: Рассмотрим составное высказывание  «2 • 2 = 4 или 2 • 2 = 5». Выделим простые выска-зывания:А = «2 • 2 = 4» = 1 (т.к. это истинное высказывание)В = «2 • 2 = 5» = 0 (т.к. это ложное высказывание)Поэтому, логическая функция F(A, B) = A \/ B = 1 \/ 0 = 1 (в соответствии с таблицей истинности), то есть данное составное высказывание истинно.

3. Отрицание (инверсия), от лат. InVersion – переворачиваю:

•    Соответствует частице НЕ, словосочетаниям НЕВЕРНО, ЧТО или НЕ ЯВЛЯЕТСЯ ИСТИНОЙ, ЧТО;•    в языках программирования — Not; •    Обозначение: не А, ¬А, not•    В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества.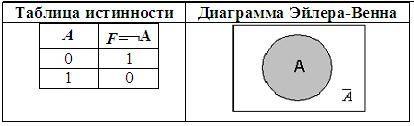

 
 
 
 
 
 
Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.

 Пример:

А = {два умножить на два равно четырем} = 1.

 ¬A= {Неверно, что два умножить на два равно четырем}= 0.

Рассмотрим высказывание А : «Луна — спутник Земли«;  тогда   ¬А будет формулироваться так:  «Луна — не спутник Земли«.

Рассмотрим высказывание: «Неверно, что 4 делится на 3». Обозначим через А простое высказывание «4 делится на 3». Тогда логическая форма отрицания этого высказывания имеет вид ¬А

Приоритет логических операций:

Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:     1. инверсия;     2. конъюнкция;     3. дизъюнкция;Для изменения указанного порядка выполнения логических операций используются круглые скобки.

Составные логические выражения алгебры высказываний называют формулами.Истинно или ложно значение формулы можно определить законами алгебры логики, не обращаясь к смыслу: F = (0 \/ 1) /\ (¬0 \/ ¬1) = (0 \/ 1) /\ (1 \/ 0) =1 /\ 1=1 — истинаF = (¬0 /\ ¬1) \/ (¬1 \/ ¬1) = (1 /\ 0) \/ (0 \/ 0) = 0 \/ 0 = 0 — ложь

Формулы логики высказываний

Понятие логической формы сложного высказывания уточняется с помощью понятия формулы
логики высказываний.

В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания.
Вообще-то они называются формулами логики высказываний.

Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы

Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные
значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее
называть их элементарными формулами или атомами.

Для построения формул логики высказываний кроме указанных выше букв используются знаки
логических операций

~, ∧, ∨, →, ,

а также символы, обеспечивающие возможность однозначного прочтения формул — левая и
правая скобки.

Понятие формулы логики высказываний определим следуюшим
образом:

1) элементарные формулы (атомы) являются формулами логики высказываний;

2) если и —
формулы логики высказываний, то , ,
, ,
тоже являются формулами логики
высказываний;

3) только те выражения являются формулами логики высказываний, для которых это
следует из 1) и 2).

Определение формулы логики высказываний содержит перечисление правил образования
этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется
из атомов в результате последовательного применения правила 2).

Пример 6. Пусть — одиночное
высказывание (атом) «Все рациональные числа являются действительными», —
«Некоторые действительные числа — рациональные числа», —
«некоторые рациональные числа являются действительными». Переведите в форму словесных высказываний
следующие формулы логики высказываний:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Решение.

1) «нет действительных чисел, которые являются рациональными»;

2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;

3) «если все рациональные числа являются действительными, то некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными»;

4) «все действительные числа — рациональные числа и некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными числами»;

5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;

6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».

Пример 7. Составьте таблицу истинности для формулы
логики высказываний , которую в
таблице можно обозначить .

Решение. Составление таблицы истинности начинаем с записи значений («истина» или «ложь»)
для одиночных высказываний (атомов) , и
. Все возможные значения записываются в восемь строк таблицы. Далее,
определяя значения операции импликации, и продвигаясь вправо по таблице, помним, что значение равно «лжи» тогда, когда из «истины» следует «ложь».

И	И	И	И	И	И	И	И
И	И	Л	И	И	И	Л	И
И	Л	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	Л	И	И
Л	И	Л	Л	И	Л	И	Л
Л	Л	И	И	И	И	И	И
Л	Л	Л	И	И	И	Л	И

Заметим, что никакой атом не имеет вида
, ,
, ,
. Такой вид имеют сложные формулы.

Число скобок в формулах логики высказываний можно уменьшить, если принять, что

1) в сложной формуле будем опускать внешнюю пару скобок;

2) упорядочим знаки логических операций «по старшинству»:

, →, ∨, ∧, ~ .

В этом списке знак имеет самую большую область действия, а знак ~ — самую
маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым
применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать
во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при
восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при
этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.

Пример 8. Восстановите скобки в формуле логики высказываний
.

Решение. Скобки восстанавливаются пошагово следующим образом:

Не всякая формула логики высказываний может быть записана без скобок. Например, в
формулах и
дальнейшее исключение скобок
невозможно.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной