Как научить ребёнка считать?

Умножение и деление на счётах

В ютубе имеется большое количество обучающих видео роликов по умножению и делению на счётах. Рекомендуется просмотреть их перед тем, как обучаться по книге.

Ментальный счет можно тренировать параллельно обучаясь умножению и делению, либо после того как обучились этому. На усмотрение преподавателя в зависимости от успеваемости группы. Нормативы тоже зависят от успеваемости учеников. В некоторых учебниках уже указаны нормативы.

Умножение на счётах основано на обычном умножении 7чисел. Ученики должны знать таблицу умножения наизусть перед тем, как начнут решать примеры на умножение на счётах.

Умножение однозначных (1дх1д) — это обычная таблица Пифагора. 2дх1д

1 пример

23×4. Точка отсчета находится примерно в середине абакуса. Имеем три цифры: 2,3,4, значит ответ откладываем на трех спицах. Откладываем слева направо.

1 действие — десяток первого множителя умножаем на другой множитель (на единицу):

2×4=08.

Правило: ЕСЛИ ОТВЕТ ОДНОЗНАЧНЫЙ, ТО ВОСПРИНИМАЕМ ЕГО КАК ДВУЗНАЧНОЕ, МЕНТАЛЬНО ПРЕДСТАВЛЯЯ ПЕРЕД НИМ 0.

На спицах слева направо откладываем 08.

Если результат откладываем на 3 спицах, в умножении откладывать нужно слева направо, значит 08 откладываем на первой и второй спицах слева, то есть на сотнях и десятках.

2 действие — единицу первого множителя умножаем на другой множитель (на единицу).

3×4=12

Откладываем 12, на второй и третьей спицах слева (на десятках и единицах).

Ответ: 92.

2 пример

65×7

— 6×7=42, откладываем на сотнях и десятках.

— 5×7=35, откладываем на десятках и сотнях.

Ответ: 455.

2дх2д

73×45

В примере 4 цифры, значит откладываем решение на 4 спицах.

— 7×4= 28 умножаем десяток одного множителя на десяток другого множителя и откладываем на 1 и 2 спицах слева направо, то есть на тысячах и сотнях.

— 7×5=35 умножаем десяток первого множителя на единицу второго множителя и откладываем на 2 и 3 спицах, то есть на сотнях и десятках.

— 3×4=12 умножаем единицу первого множителя на десяток второго множителя и откладываем на 2 и 3 спицах, то есть на сотнях и десятках.

— 3×5=15 умножаем единицу первого множителя на единицу другого множителя и откладываем на 3 и 4 спицах, то есть на десятках и единицах..

Ответ: 3285.

3дх2д

926×52

В примере 5 цифр, значит откладываем результат на 5 спицах слева направо.

— 9×5=45 умножаем сотню первого множителя на десяток второго множителя и откладываем на 1 и 2 спицах слева направо, то есть на десятках тысячах и на тысячах.

— 9×2=18 умножаем сотню первого множителя на единицу второго множителя и откладываем на 2 и 3 спицах слева направо, то есть на тысячах и на сотнях.

— 2×5=10 умножаем десяток первого множителя на десяток второго множителя и откладываем на 2 и 3 спицах слева направо, то есть на тысячах и сотнях.

— 2×2=4 умножаем десяток первого множителя на единицу второго множителя и откладываем на 3 и 4 спицах слева направо, то есть на сотнях и десятках.

— 6×5=30 умножаем единицу первого множителя на десяток второго множителя и откладываем на 3 и 4 спицах слева направо, то есть на сотнях и десятках.

— 6×2=12 умножаем единицу первого множителя на единицу второго множителя и откладываем на 4 и 5 спицах слева направо, то есть на десятках и единицах.

Решение более сложных примеров на умножение на счётах является аналогичным. Чтобы запомнить алгоритм откладывания ответа на абакусе, нужна практика и скорость.

Игра «Магазин»

Чтобы научить ребенка считать, следует проводить с ним различные игры. Это позволит малышу лучше усвоить материал. Идеальной игрой для развития навыков счета является «Магазин». Для начала помогите ребенку создать свою торговую лавку. Для этого, конечно же, потребуется различный товар. Это могут быть игрушки, книги, карандаши и прочее. К каждому товару стоит прикрепить его название и цену. Попутно можете ребенку рассказать, что такое стоимость товара и всегда ли она определяется размерами изделия. Эти знания также пригодятся ребенку в жизни.

Помимо этого, родителям стоит изготовить бумажные деньги для оплаты покупок. После этого можно приступить к игре. В магазине вы можете приобрести несколько книг, скажем, по 6 рублей. Ребенок должен сосчитать это все на счетах. Оплатите покупку так, чтобы малыш должен был дать сдачи.

Эта игра позволит решить примеры не только на сложение, но и на вычитание. Также можно поиграть в игру, которая позволит развить у ребенка память. Для этого можно разместить определенное количество костяшек и дать время ребенку это запомнить. После этого малыш должен самостоятельно выложить такой же узор.

Что важно в занятиях

Конечно, перед тем как начать проводить с ребенком занятия, необходимо знать, как пользоваться счетами деревянными. При правильной работе малыш получает не только полезные навыки, но и умения.

При проведении занятий стоит следить за тем, чтобы они были направлены на гармоничное, комплексное развитие. Иными словами, работать с малышом нужно так, чтобы он не уставал, делая одно и то же по несколько раз. Нередко родители усиленно развивают у ребенка логику, совершенно забывая о фантазии, которая в дальнейшем ему еще пригодится, и не только в школе, но и в реальной жизни. Старайтесь не допускать подобных ошибок.

Условия пользования

В течение 1-2 дней вы получите СМС и письмо на почту об открытии счета. Только после этого можно вносить деньги и совершать первые операции на бирже. Из присланных сообщений можно узнать номер договора на обслуживание. Он потребуется для входа в мобильное приложение для торговли “Сбербанк Инвестор”.

Далее рассмотрим особенности двух тарифов, условия внесения денег, процедуру купли-продажи ценных бумаг.

Тарифы

Для физического лица доступны 2 тарифа:

1. Самостоятельный – отличный старт для новичков. Минимальные комиссии за сделку, нет платы за обслуживание счета.
2. Инвестиционный – для опытных инвесторов. Комиссии выше, но есть регулярная инвестиционная рассылка от команды аналитиков Сбербанка. Доступ к ежедневным обзорам по инструментам получают только квалифицированные инвесторы.

Сравнение комиссий в таблице:

Комиссии	Самостоятельный	Инвестиционный
За совершение сделок на фондовом рынке:
	0,06 %	0,3 %
	0,035 %	0,3 %
	0,018 %	0,3 %
За совершение сделок на валютном рынке:
	0,2 %	0,2 %
	0,02 %	0,2 %
За совершение сделок на срочном рынке	0,5 руб. за контракт	0,5 руб. за контракт
Подача заявок по телефону (комиссия берется с 21-го поручения в течение месяца)	150 руб.	150 руб.

Минимального депозита на тарифах нет. Можно пополнить счет хоть на 1 000 руб. и купить свою первую акцию. Дополнительно взимается комиссия биржи в размере 0,01 % от объема сделки.

Как пополнить счет

Пополнить брокерский счет удобнее через интернет (мобильное приложение или “Сбербанк Онлайн”). Рассмотрим на примере смартфона.

Шаг 1. В мобильном приложении выбрать вкладку “Инвестиции и пенсии” и счет, который будете пополнять.

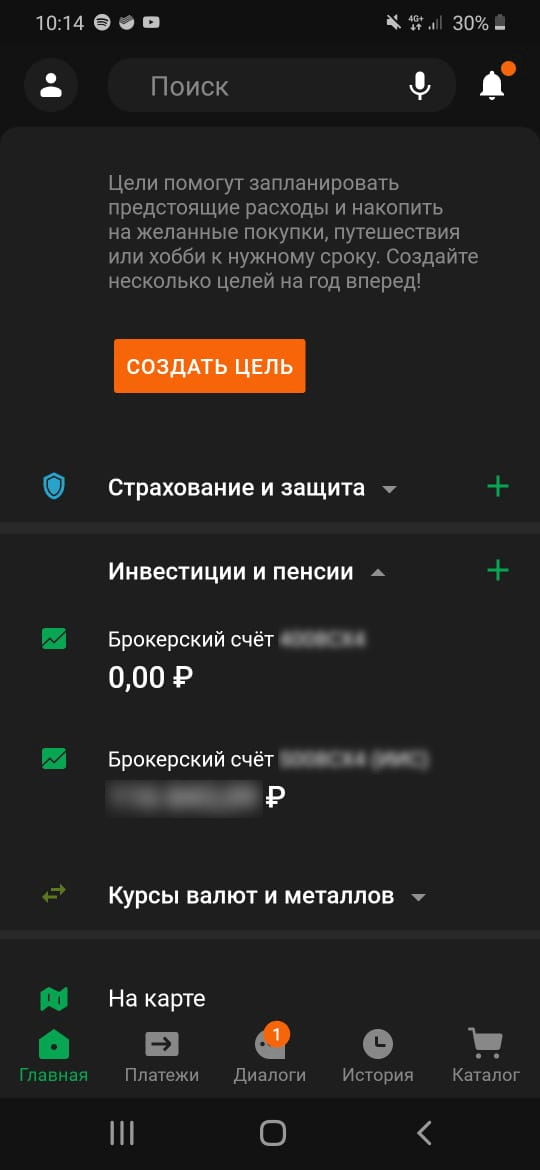
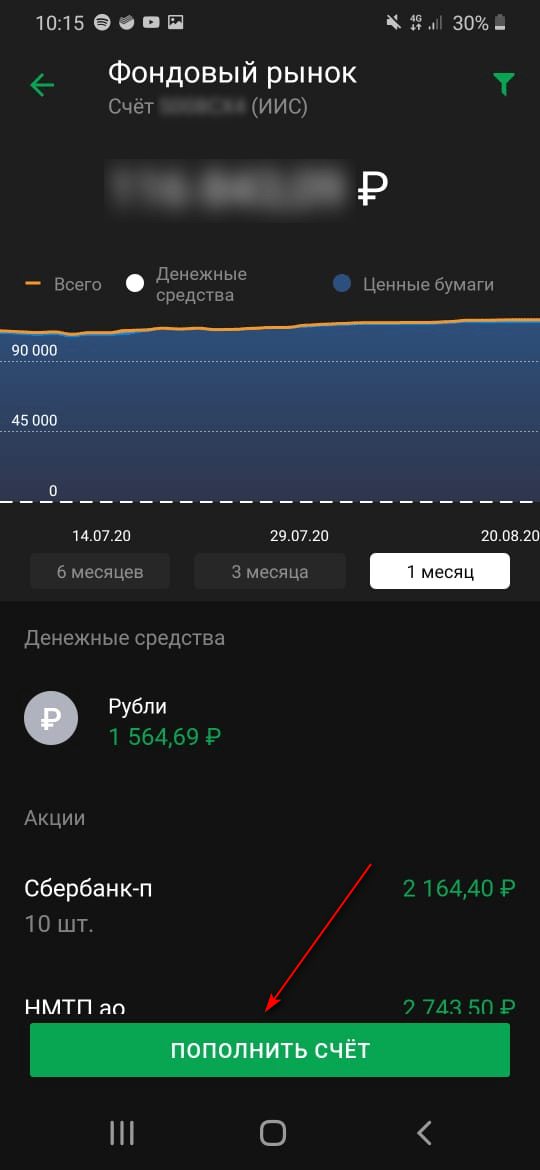
Шаг 2. Выбрать рынок, на котором будут осуществляться сделки, номер банковской карты и сумму пополнения.

Шаг 3. Нажать на кнопку “Пополнить счет”. Деньги приходят моментально.

Как покупать и продавать ценные бумаги

Самые большие неудобства для инвесторов скрываются именно в процедуре купли-продажи ценных бумаг. Есть 2 возможности: мобильное приложение “Сбербанк Инвестор” и торговая платформа QUIK. Остановимся подробнее на первом варианте, потому что второй не зависит от брокера – программа одинаковая для всех.

К сожалению, компьютерной версии собственной торговой платформы у Сбербанка нет, только мобильное приложение, которое мало кому нравится. Главные недостатки – это отсутствие биржевого стакана, где можно посмотреть актуальные цены спроса и предложения на ценные бумаги, и особенности формирования рыночной цены.

Рассмотрим на скринах, как купить акцию (продажа проводится аналогично).

Шаг 1. Вход в приложение происходит по номеру договора и паролю. Надо выбрать вкладку “Рынок”.

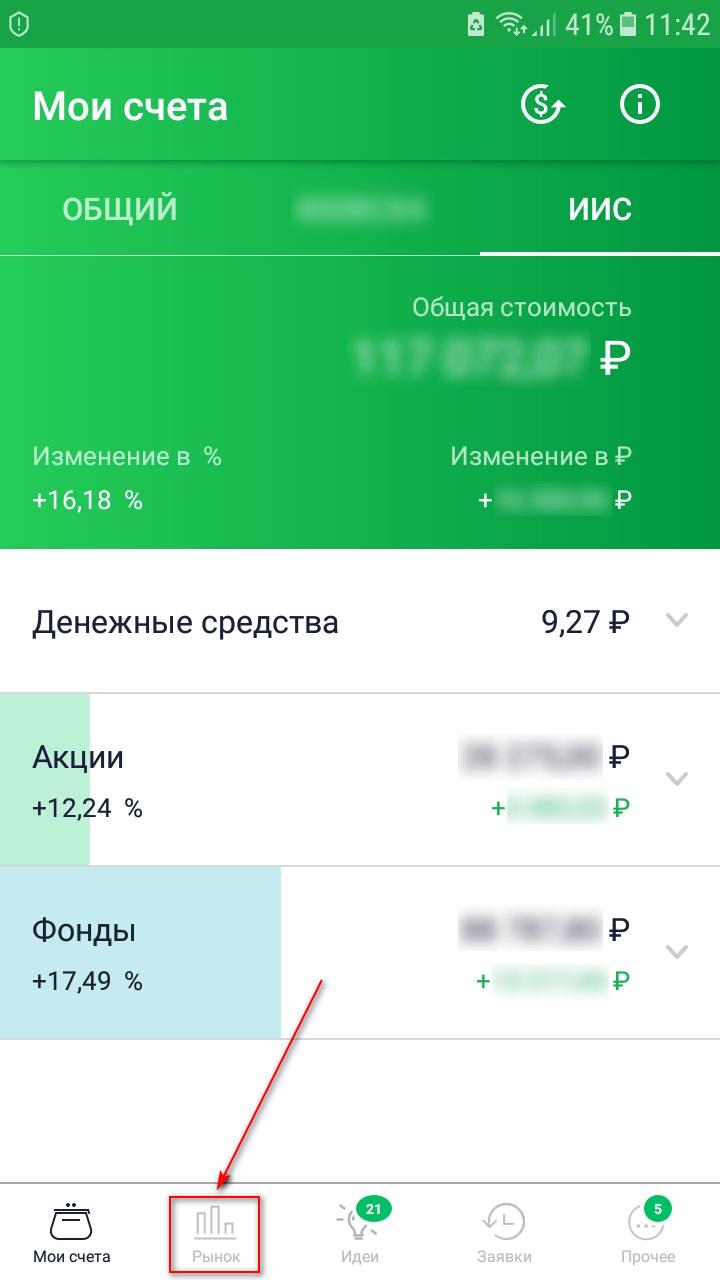
Шаг 2. Из предложенного списка акций, облигаций, фондов и валюты выбираем нужную позицию. Я для примера взяла привилегированную акцию Сбербанка.

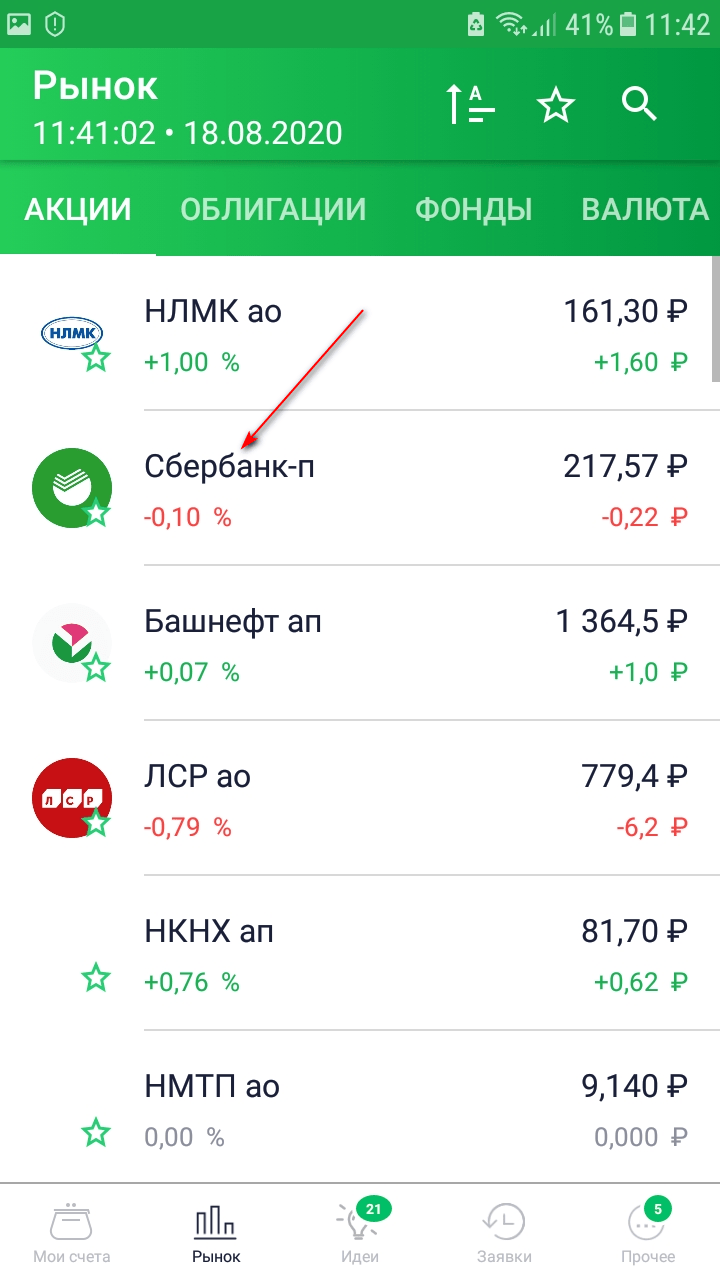
Шаг 3. Изучаем аналитику по выбранному инструменту и нажимаем кнопку “Купить”.

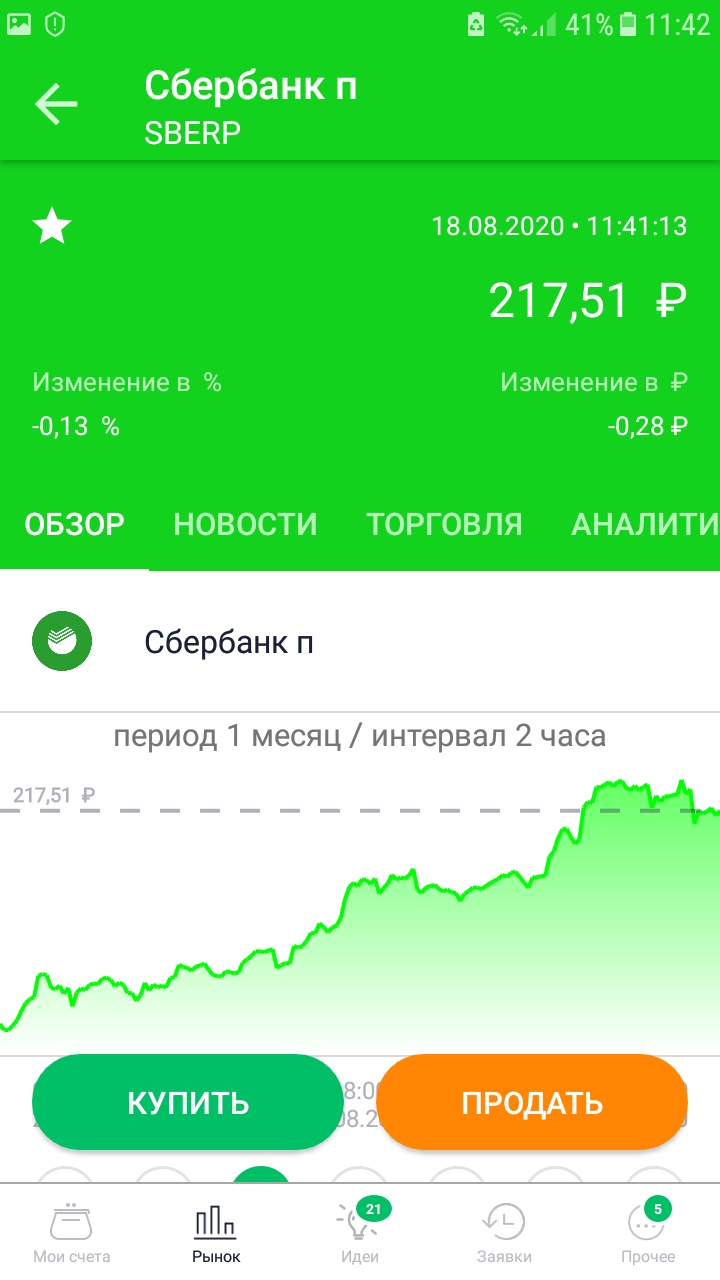
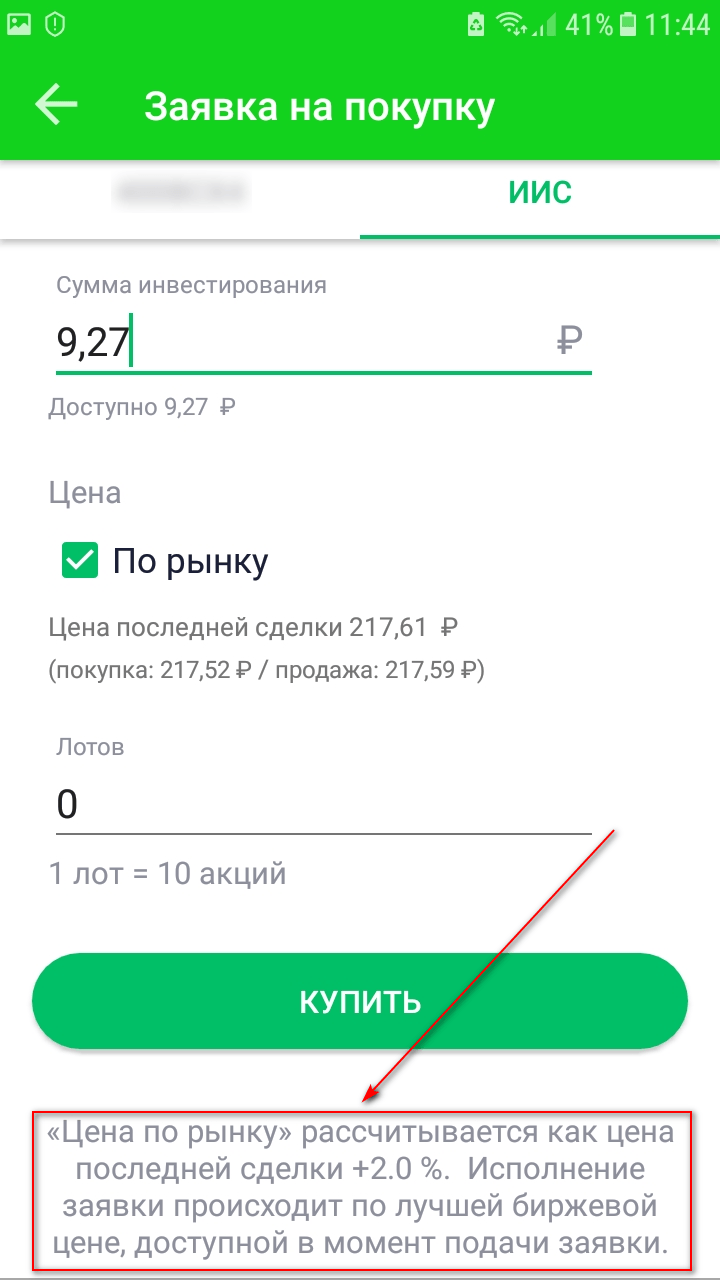
Шаг 4. А теперь самый важный момент. Внимательно читаем, что написано в самом низу экрана. Рыночная цена устанавливается как цена последней сделки + 2 %. На скрине ниже цена последней сделки была 217,61 руб. Цена по рынку будет – 221,96 руб. Если вы оставите галочку в поле (она стоит по умолчанию), то купите акцию за 221,96 руб. Если галочку уберете, то сможете выставить свою цену, как минимум уменьшив ее на 2 %. Я всегда ориентируюсь на биржевой стакан. У Сбербанка его нет, поэтому приходится смотреть у другого моего брокера.

Не рекомендую в приложении “Сбербанк Инвестор” покупать или продавать акции “по рынку”. Всегда пользуйтесь лимитированной заявкой, т. е. самостоятельно назначайте цену. Такой проблемы не будет, если пользоваться платформой QUIK (там есть стакан). Но не все новички ею пользуются.

Сложение и вычитание

В youtube большое количество видеоуроков по ментальной арифметике. Перед решением примеров на отработку формул, рекомендую изучить теорию

Также обучиться формулам бесплатно и набрать скорость в счете на абакусе можно при помощи приложения для Android Simple Soroban (в отличие от других аналогичных приложений в Simple Soroban можно одновременно перемещать несколько косточек, что очень важно в технике пальцев). Формулы для решения примеров на абакусе до 5 называют младшими товарищами, до 10 старшими товарищами, составные формулы микс формулами

Некоторые центры называют их друзьями, семьей и т. д. Суть не в названии. За 2000 лет формулы не изменились. Главное их понять и набрать скорость как при решении на счётах, так и в ментальном счете.

План обучения преподавателей:

— прямой счет на однозначных числах

— младшие товарищи

— старшие товарищи

— двузначные числа

— составные формулы

— переход на 50, 100

— трехзначные

— подготовка к умножению и делению, умножение и деление на абакусе.

Фундаментальные упражнения на отработку составных формул.

+6=-5+1+10

5+6, 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6, 26+6, 27+6, 28+6, 35+6, 36+6, 36+6, 37+6, 38+6

+7=-5+2+10

5+7, 6+7, 7+7, 15+7, 16+7, 17+7, 25+7, 26+7, 27+7, 35+7, 36+7, 37+7

+8=-5+3+10

5+8, 6+8, 15+8, 16+8, 25+8, 26+8, 35+8, 36+8

+9=-5+4+10

5+9, 15+9, 25+9, 35+9, 55+9, 65+9, 75+9, 85+9

— 6=-10+5—1

11–6, 12–6, 13–6, 14–6, 21–6, 22–6, 23–6, 24–6, 31–6, 32–6, 33–6, 34–6, 41–6, 42–6, 43–6, 44–6

— 7=-10+5—2

12–7, 13–7, 14–7, 22–7, 23–7, 24–7, 32–7, 33–7, 34–7, 42–7, 43–7, 44–7

— 8=-10+5—3

13–8, 14–8, 23–8, 24–8, 33–8, 34–8, 43–8, 44–8, 63–8, 64–8, 73–8, 74–8, 83–8, 84–8, 93–8, 94–8

— 9=-10+5—4

14–9, 24–9, 34–9, 44–9, 64–9, 74–9, 84–9, 94–9

Фундаментальные упражнения на отработку формул старших товарищей (минус) −9=-10+1

10–9, 11–9, 12–9, 13–9, 15–9, 16–9, 17–9, 18–9, 20–9, 21–9, 22–9, 23–9, 25–9, 26–9, 27–9, 28–9

— 8=-10+2

10–8, 11–8, 12–8, 20–8, 21–8, 22–8, 30–8, 31–8, 32–8, 40–8, 41–8, 42–8

— 7=-10+3

10–7, 11–7, 20–7, 21–7, 30–7, 31–7, 40–7, 41–7, 60–7, 61–7, 70–7, 71–7, 80–7, 81–7, 90–7, 91–7

— 6=-10+4

10–6, 15–6, 20–6, 25–6, 30–6, 35–6, 40–6, 45–6, 60–6, 65–6, 70–6, 75–6, 80–6, 85–6, 90–6, 95–6

— 5=-10+5

10–5, 11–5, 12–5, 13–5, 14–5, 20–5, 21–5, 22–5, 23–5, 24–5, 30–5, 31–5, 32–5, 33–5, 34–5, 41–5, 42–5,

43–5, 44–5

— 4=-10+6

10–4, 11–4, 12–4, 13–4, 20–4, 21–4, 22–4, 23–4, 30–4, 31–4, 32–4, 33–4, 40–4, 41–4, 42–4, 43–4

— 3=-10+7

10–3, 11–3, 12–3, 20–3, 21–3, 22–3, 30–3, 31–3, 32–3, 40–3, 41–3, 42–3

— 2=-10+8

10–2, 11–2, 20–2, 21–2, 30–2, 31–2, 40–2, 41–2, 60–2, 61–2

— 1=-10+9

10–1, 20–1, 30–1, 40–1, 60–1, 70–1, 80–1, 90–1

Переход через 50

+50

41+9

42+9 42+8

43+9 43+8 43+7

44+9 44+8 44+7 44+6

45+9 45+8 45+7 45+6 45+5

46+9 46+8 46+7 46+6 46+5 46+4

47+9 47+8 47+7 47+6 47+5 47+4 47+3

48+9 48+8 48+7 48+6 48+5 48+4 48+3 48+2

49+9 49+8 49+7 49+6 49+5 49+4 49+3 49+2 49+1

— 50

50–9 50–8 50–7 50–6 50–5 50–4 50–3 50–2 50–1

51–9 51–8 51–7 51–6 51–5 51–4 51–3 51–2

52–9 52–8 52–7 52–6 52–5 52–4 52–3

53–9 53–8 53–7 53–6 53–5 53–4

54–9 54–8 54–7 54–6 54–5

55–9 55–8 55–7 55–6

56–9 56–8 56–7

57–9 57–8

58–9

Переход через 100

+100

91+9

92+9 92+8

93+9 93+8 93+7

94+9 94+8 94+7 94+6

95+9 95+8 95+7 95+6 95+5

96+9 96+8 96+7 96+6 96+5 96+4

97+9 97+8 97+7 97+6 97+5 97+4 97+3

98+9 98+8 98+7 98+6 98+5 98+4 98+3 98+2

99+9 99+8 99+7 99+6 99+5 99+4 99+3 99+2 99+1

— 100

100–9 100–8 100–7 100–6 100–5 100–4 100–3 100–2 100–1

101–9 101–8 101–7 101–6 101–5 101–4 101–3 101–2

102–9 102–8 102–7 102–6 102–5 102–4 102–3

103–9 103–8 103–7 103–6 103–5 103–4

104–9 104–8 104–7 104–6 104–5

105–9 105–8 105–7 105–6

106–9 106–8 106–7

107–9 107–8

108–9

Составные формулы (микс формулы)

В начале объяснения этой темы напишите формулу на доске: «+6 = +10 −5 +1». Дальше говорим: «Ребята, число 6 на абакусе выглядит так: 5 и 1, верно? Шесть — это пять и одна косточка снизу. Мы это все знаем. А чтобы на абакусе 5 прибавить 6, мы используем микс формулу, которая написана на доске (также на доске напишите пример: 5 +6 = _____). Смотрите: „+6 = +10 −5 +1“. Давайте я покажу как решить такой пример на большом абакусе, а вы повторяйте за мной в воздухе. Чтобы к 5 прибавить 6, мы левой рукой прибавляем 10, а правой делаем одновременно −5 +1. Сколько получилось? 11! Правильно! (дописываем на доске ответ 5 +6=11, и решаем на большом абакусе примеры: 6+6, 7+6, 8+6, 15+6, 16+6, 17+6, 18+6, 25+6 и т. д. Дети повторяют в воздухе за учителем. Сначала пример пишем на доске потом только показываем решение на большом абакусе. Затем все дети делают ФУ на микс формулы под диктовку учителя:5+6, 15+6, 26+6, 17+6, 8+6 и так далее. После ФУ по два-три ученика выходят решать на большом абакусе).

Теперь посмотрите какую формулу я написала на доске: +7 = +10 −5 +2. Знаете почему +2? Потому что число 7 на счётах — это 5 плюс 2. Все поняли? Молодцы! Давайте решим пример: 5+7=_____. Чтобы решить такой пример нам поможет микс формула. Давайте я покажу как решить такой пример на большом абакусе, а вы повторяйте за мной в воздухе. Чтобы к 5 прибавить 7, мы левой рукой прибавляем 10, а правой делаем одновременно −5 +2. Сколько получилось? 12! Правильно! Теперь я покажу как решить такой пример: 6+7, повторяем за мной в воздухе (показываем несколько примеров на доске и большом абакусе. Следим, чтобы дети повторяли в воздухе. Затем под диктовку учителя ФУ: 5+7, 6+7, 7+7, 15+7, 16+7, 17+7 и т. д. После этого по два-три ученика на большом абакусе решаем примеры)».

Аналогично обучаем формуле +8 = +10 −5 +3. Почему +3? Потому что 8 на счётах — это 5 плюс 3. Также и формула +9 = +10 −5 +4, так как 9 на счётах — это 5 плюс 4.

На минус микс формулы нужно обратить особое внимание, так как формулы на минус иногда воспринимается сложнее:

— 6 = −10 +5 −1

— 7 = −10 +5 −2

— 8 = −10 +5 −3

— 9 = −10 +5 −4

1.11 Экзамен ученика после каждого уровня

После завершения каждого уровня ученики сдают экзамен.

Преподаватель фиксирует время и записывает результаты.

План проведения экзамена:

1) За 30 минут до конца урока раздаем экзаменационные листочки детям. Ученики пишут имена, фамилии и дату на экзаменационных листочках.

2) Затем ученики записывают состав чисел 5 и 10.

3) Повторяем правила диктанта и правило одинаковых знаков. Засекаем время и начинаем диктант. Диктовать нужно чуть медленнее чем на занятиях. Примеры должны быть на все пройденные темы.

4) Ученики одновременно под команду учителя (засекаем время на секундомере) начинают решать примеры. Заранее нужно сообщить детям, что экзамен проверяется на ошибки и на скорость.

Сдавшим экзамен считается тот ученик, который решил примеры за нужное время и с количеством ошибок менее 20%. Время, за которое ученик должен решить примеры экзамена, зависит от возраста ученика. Нормативы устанавливаются каждым центром индивидуально.

Пересдача экзамена допустима один раз. При провале экзамена если причиной провала было отсутствие скорости, то ученик может продолжить обучение следующего уровня ментальной арифметики вместе со своей группой.

При провале экзамена если причиной провала было большое количество ошибок, отсутствие скорости, незнание формул, пропуски и так далее, то ученику предлагают заново пройти первый уровень с другой группой или присоединится к другой группе, которая проходит ту, тему с которой этот ученик стал отставать.

Как умножать и делить на абакусе?

Умножение на линейке тоже достаточно простое, для этого нужно только освоить таблицу умножения от 1 до 10 и запомнить одно правило: десятки умножаем на единицы, потом единицы умножаем на единицы. Если ребенок уже разобрался, как считать на абакусе, все действия будут занимать не больше минуты.

Для примера возьмем простое задание 11х5, которое решается в два действия:

1. 10х5=50.
2. 1х5=5.

Для начала на абакусе набирается ответ на первый пример, 50:

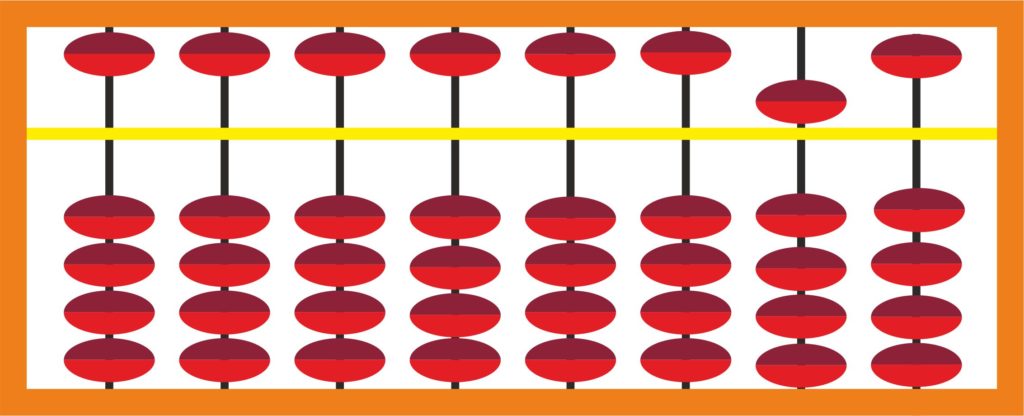
потом к нему добавляется ответ на второй пример, 5:

И в результате мы видим на абаке ответ 55.

Для проведения более сложных действий, когда берутся более сложные примеры, тогда задание решается в последовательности: десятки умножаются на десятки, единицы на десятки, десятки на единицы, единицы на единицы. То есть, сначала все цифры, постепенно от большего к меньшему перемножаются и набираются последовательно на абаке.

Например, 611 Х24:

Решается это так, нули прячутся и берутся цифры без них, а их количество определяет, на сколько спиц надо сдвинуться влево, кроме того, если результат получился двузначный, значит надо сместиться еще на одну спицу:

1. 6х2=12 – при умножении результат набираем на той спице, к которой относится число и сдвигаемся вправо на столько спиц, сколько нулей в числе, на которое умножают, в нашем случае в 20 один ноль, то есть результат 12 набирается не на сотнях, а на тысячах. Но если результат имеет две цифры, тогда надо сместиться еще на одну спицу. То есть, в нашем случае 12 набирается на спицах, отвечающих на десять тысяч и тысячи.(12000)
2. 1х2=2 – единица относится к десяткам, в 20 один ноль, то есть сдвигаемся на одну спицу и добавляем ответ в сотнях.(12200)

1х2=2 единица относится к единицам, а в 20 один ноль, то есть исходя из правил, добавляем ответ в десятках.(12220)

1. Теперь переходим к следующему порядку и умножаем сотни на единицы, десятки на единицы и единицы на единицы.
2. 6х4=24 – в 4 нет нолей, мы сдвигаемся только на одну спицу, так как в ответе две цифры, и добавляем 2 костяшки к тысячам и 4 к сотням. (14620)
3. 1х4=4 – добавляем в десятки 4 костяшки. (14660)
4. 1х4=добавляем теперь 4 костяшки в единицы. (14664)

Последнее действие можно не делать, но сначала нужно проверить: берем калькулятор, умножаем 611х24, получаем 14664 и радуемся своей сноровке.

Деление проводится по такому же принципу, только производится не сложение результатов на линейке, а вычитание. Сдвигание по спицам происходит слева направо.

Усовершенствование

На протяжении четверти тысячелетия популярности и практической необходимости счет неоднократно предпринимались (часто закончившиеся удачно), попытки усовершенствовать русские счеты. Остановимся только на одной из них. В 1828 г. генерал-майор Ф. М. Свободский представил в соответствующую инстанцию счетный прибор, который не только осуществлял привычные для русских счет действия, но достаточно быстро извлекал кубические корни, возводил числа в степень, вычислял сложные проценты и так далее. Достигалось это только методами сложения и вычитания с фиксацией промежуточных результатов на специальном поле счет. Однако скорость получения искомого результата так поразила комиссию, что она рекомендовала данный прибор к производству и введению специального курса в военных заведениях. Но до реального исполнения решения дело не дошло.

В настоящее время в России счеты применяются только в качестве музейного экспоната или семейной реликвии. Очень редко, если они наличествуют у кого-то в доме, могут использоваться подрастающим поколением для катания по полу, или старшими для массажа ног или спины. А зря! В современном Китае на «Суаньпань» учат учеников младших классов, так как считается, что освоивший такой способ счета ребенок развивается лучше и быстрее, не научившегося работать на этом древнем приспособлении.

Деление

Как умножение заменяется многократным сложением, так и деление на счетах – это постоянное вычитание. Начинается все с верхнего разряда и идет вниз. Переносится направо число косточек, равных делителю (каждый раз, как это удается на самой верхней проволочке, переносится одна косточка налево) до тех пор, пока слева не окажется косточек меньше чем число, на которое производится деление (делитель).

Затем к процессу подключается нижеследующий разряд. И если в предыдущей проволочке остались косточки, то вычитается делитель уже из двузначного числа. Если нет, то, как в предыдущий раз. Если в низшем разряде вычитание пройдет без остатка косточек слева, то значит деление произведено без остатка. Если слева косточки остались, то в случае необязательного получения в итоге дробного числа – остаток игнорируется, а если обязательно его получение, то вычитание продолжается до нужной точности на прутьях ниже РР, с указанием дробного разделителя на бумаге. Аналогично производится деление на двухзначные, трехзначные (и т. д.) числа, только сначала вычитание идет из соответственно двух, трех и так далее высших разрядов.

Умножение

Изучение принципа умножения на абакусе чуть сложнее, чем предыдущие задачи. Придется немного напрячься. Начинайте перемножать с большего разряда, двигаясь от сотен к единицам поэтапно. Большой палец двигает костяшки вверх, указательный – вниз.

Вначале советуем вам посмотреть обучающее видео на эту тему:

И еще один дополнительный урок по умножению:

Умножим 13 на 22

1. Сначала берем десятки у обеих цифр. Умножаем устно: 10 x 20 = 200.
2. Откладываем получившийся результат на счетах.
3. Теперь действуем так же с единицами первого числа и десятками второго. Умножаем 3 x 20 = 60.
4. Откладываем на счетах.
5. На этом этапе берем десятки первого числа и перемножаем с единицами второго. 10 x 2 = 20.
6. Передвигаем костяшки.
7. Осталось перемножить единицы обеих цифр: 3 x 2 = 6.
8. Откладываем и оцениваем результат на счетах.
9. Получилось 286.

Дополнительные числа

Высокая скорость работы на соробане зависит от того, насколько механизированы действия считающего. Смысл заключается в том, чтобы снять лишнюю нагрузку с ума и выполнять арифметические действия механически, без размышлений или колебаний, отсюда и сравнение людей, обладающих этим навыком, с калькулятором. И если со сложением и вычитанием простых чисел всё ясно, то с более сложными примерами нужно освоить концепцию дополнительных чисел. Нужно просто запомнить, что:

• цифру 5 можно разложить на дополнительные числа: 4 и 1, 5 и 2.
• цифру 10 можно разложить на дополнительные числа: 9 и 1, 8 и 2, 7 и 3, 6 и 4, 5 и 5.

При сложении дополнительное число вычитается. При вычитании — дополнительное число прибавляется. Как это работает на практике рассмотрим далее.

Можно ли заниматься дома

Обучать малышей счету на абакусе не обязательно в специализированных центрах. Если родители мобильны, готовы тратить время и силы на самообразование и развитие детей, то домашние занятия по ментальной арифметике станут не только хобби, но и семейным видом общения, игр.

Сторонники развивающих уроков дома с мамой настаивают на нескольких плюсах и минусах самостоятельного непрофессионального обучения.

Преимущества

• Знакомая обстановка помогает расслабиться, дети не испытывают стресса.
• Родители учитывают индивидуальные особенности малыша при планировании занятий.
• Отсутствие платы за обучение.
• Экономия времени. Добираться до обучающих центров не нужно.
• Самообразование для родителей.

Недостатки

• Отсутствие опыта у домашних педагогов.
• Минимальное количество информации о методе в Сети, книжных магазинах. Педагоги спеццентров стараются держать тонкости преподавания в тайне.

Занятия ментальной арифметикой дома – неплохой способ саморазвития и обучения ребенка. Но решаться на этот шаг нужно при хорошей дидактической, методологической подготовке родителей. Иначе вы рискуете совершить массу ошибок.

А исправлять недочеты гораздо сложнее, чем сразу научить правильно.

С чего начать обучение счету

На первом этапе обучения устному счету необходимо научить ребенка считать в пределах десяти. Нужно помочь ему прочно запомнить результаты всех вариантов сложения и вычитания чисел в пределах десяти так, как помним их мы, взрослые.

На втором этапе обучения дошкольники осваивают основные методы сложения и вычитания в уме двузначных чисел. Главным теперь уже является не автоматическое извлечение из памяти готовых решений, а понимание и запоминание способов сложения и вычитания в последующих десятках.

Как на первом, так и на втором этапе обучение устному счету происходит с применением элементов игры и состязательности. С помощью обучающих игр, выстроенных в определенной последовательности, достигается не формальное заучивание, а осознанное запоминание с использованием зрительной и тактильной памяти ребенка с последующим закреплением в памяти каждого усвоенного шага.

Почему я учу именно устному счету? Потому что только устный счет развивает память, интеллект ребенка и то, что мы называем смекалкой. А именно это и потребуется ему в последующей взрослой жизни. А писание «примеров» с длительным обдумыванием и вычислением ответа на пальчиках дошкольнику ничего, кроме вреда, не приносит, т.к. отучает думать быстро. Примеры он будет решать позже, в школе, отрабатывая аккуратность оформления. А сообразительность необходимо развить в раннем возрасте, чему способствует именно устный счет.

Еще до того как начать обучение ребенка сложению и вычитанию, родители должны научить его пересчитывать предметы на картинках и в натуре, считать ступеньки на лестнице, шаги на прогулке. К началу обучения устному счету ребенок должен уметь сосчитать хотя бы пять игрушек, рыбок, птичек, или божьих коровок и при этом освоить понятия «больше» и «меньше». Но все эти разнообразные предметы и существа не следует использовать в дальнейшем для обучения сложению и вычитанию. Обучение устному счету нужно начинать со сложения и вычитания одних и тех же однородных предметов, образующих определенную конфигурацию для каждого их числа. Это позволит задействовать зрительную и тактильную память ребенка при запоминании результатов сложения и вычитания целыми числовыми группами (см. видеофайл 056). В качестве пособия для обучения устному счету я применил набор небольших счетных кубиков в коробочке для счета (подробное описание — далее). А к рыбкам, птичкам, куклам, божьим коровкам и прочим предметам и существам дети вернутся позже, при решении арифметических задач. Но к этому времени сложение и вычитание любых чисел в уме уже не будет представлять для них сложности.

Для удобства изложения я разбил первый этап обучения (счет в пределах первого десятка) на 40 уроков, а второй этап обучения (счет в последующих десятках) еще на 10-15 уроков. Пусть вас не пугает большое количество уроков. Разбивка всего курса обучения на уроки приблизительна, с подготовленными детьми я прохожу иногда по 2-3 урока за одно занятие, и вполне возможно, что вашему малышу так много занятий не потребуется. Кроме того, уроками эти занятия можно назвать лишь условно, т.к. продолжительность каждого составляет лишь 10-20 минут. Их можно также совмещать с уроками чтения. Заниматься желательно два раза в неделю, а выполнению домашних заданий достаточно уделять по 5-7 минут в остальные дни. Самый первый урок нужен не каждому ребенку, он разработан лишь для детей, которые еще не знают цифры 1 и, глядя на два предмета, не могут сказать, сколько их, не подсчитав предварительно пальчиком. Их обучение необходимо начинать практически «с чистого листа». Более подготовленные дети могут начинать сразу со второго, а некоторые — с третьего или четвертого урока.

Я провожу занятия одновременно с тремя детьми, не более, чтобы удерживать внимание каждого из них и не давать им скучать. Когда уровень подготовки детей несколько отличается, приходится заниматься с ними поочередно разными задачками, все время переключаясь с одного ребенка на другого

На начальных уроках присутствие родителей желательно для того, чтобы они поняли суть методики и правильно выполняли несложные и коротенькие ежедневные домашние задания со своими детьми. Но разместить родителей надо так, чтобы дети забыли об их присутствии. Родители не должны вмешиваться и одергивать своих детей, даже если те шалят или отвлекаются.

Занятия с детьми устным счетом в небольшой группе можно начинать, приблизительно, с трехлетнего возраста, если они уже умеют подсчитывать пальчиком предметы, хотя бы до пяти. А с собственным ребенком родители вполне могут заниматься начальными уроками по этой методике и с двух лет.