Почему нельзя в математике делить на ноль: формула и правило доказательства

Действия с нулем

Для начала необходимо определить, какие действия с нулем можно выполнять. Существует несколько видов действий:

• Сложение,
• Умножение,
• Вычитание,
• Деление (ноля на число),
• Возведение в степень.

Важно! Если при сложении к любому числу прибавить ноль, то это число останется прежним и не поменяет своего числового значения. То же произойдет, если от любого числа отнять ноль

При умножении и делении все обстоит немного иначе. Если умножить любое число на ноль, то и произведение тоже станет нулевым.

Рассмотрим пример:

0*5=0

Запишем это как сложение:

0+0+0+0+0=0

Всего складываемых нолей пять, вот и получается, что

0*5=0

Попробуем один умножить на ноль. Результат также будет нулевым.

Ноль также можно разделить на любое другое число, не равное ему. В этом случае получится дробь, значение которой также будет нулевым. Это же правило действует и для отрицательных чисел. Если ноль делить на отрицательное число, то получится ноль.

0:(-5)=0

Также можно возвести любое число в нулевую степень. В таком случае получится 1

При этом важно помнить, что выражение «ноль в нулевой степени» абсолютно бессмысленно. Если попытаться возвести ноль в любую степень, то получится ноль

Пример:

04=0*0*0*0

Пользуемся правилом умножения, получаем 0.

Так можно ли делить на ноль

Итак, вот мы и подошли к главному вопросу. Можно ли делить на ноль вообще? И почему же нельзя разделить число на ноль при том, что все остальные действия с нулем вполне существуют и применяются? Для ответа на этот вопрос необходимо обратиться к высшей математике.

Начнем вообще с определения понятия, что же такое ноль? Школьные учителя утверждают, что ноль-это ничто. Пустота. То есть когда ты говоришь, что у тебя 0 ручек, это значит, что у тебя совсем нет ручек.

В высшей математике понятие «ноль» более широкое. Оно вовсе не означает пустоту. Здесь ноль называют неопределенностью, так как если провести небольшое исследование, то получается, что при делении ноля на ноль мы можем в результате получить любое другое число, которое не обязательно может быть нолем.

Знаете ли вы, что те простые арифметические действия, которые вы изучали в школе не так равноправны между собой? Самыми базовыми действиями являются сложение и умножение.

Для математиков не существует понятий «деление» и «вычитание». Допустим: если от пяти отнять три, то останется два. Так выглядит вычитание. Однако, математики запишут это таким образом:

Х+3=5

Таким образом, получается, что неизвестной разностью является некое число, которое нужно прибавить к 3, чтобы получить 5. То есть, не нужно ничего вычитать, нужно просто найти подходящее число. Это правило действует для сложения.

Немного иначе дела обстоят с правилами умножения и деления. Известно, что умножение на ноль приводит к нулевому результату. Например, если 3:0=х, тогда, если перевернуть запись, получится 3*х=0. А число, которое умножалось на 0 даст ноль и в произведении. Получается, что числа, которое бы давало в произведении с нолем какую-либо величину, отличную от ноля, не существует. А значит, деление на ноль бессмысленно, то есть оно подходит к нашему правилу.

Но что будет, если попытаться разделить сам ноль на себя же? Возьмем как х некое неопределенное число. Получается уравнение 0*х=0. Его можно решить.

Если мы попробуем взять вместо х ноль, то мы получим 0:0=0. Казалось бы, логично? Но если мы попробуем вместо х взять любое другое число, например, 1, то в конечном итоге получится 0:0=1. Та же ситуация будет, если взять любое другое число и подставить его в уравнение.

В этом случае получится, что мы можем как множитель взять любое другое число. Итогом будет бесконечное множество разных чисел. Порой все же деление на 0 в высшей математике имеет смысл, но тогда обычно появляется некое условие, благодаря которому мы сможем все-таки выбрать одно подходящее число. Это действие называется «раскрытием неопределенности». В обычной же арифметике деление на ноль снова потеряет свой смысл, так как мы не сможем выбрать из множества какое-то одно число.

Важно! На ноль нельзя разделить ноль

Деление

Из всего вышеперечисленного вытекает и другое важное правило:

Это правило нам тоже с самого детства упорно вбивают в голову. Мы просто знаем, что нельзя и всё, не забивая себе голову лишней информацией. Если вам неожиданно зададут вопрос, по какой причине запрещено делить на ноль, то большинство растеряется и не сможет внятно ответить на простейший вопрос из школьной программы, потому что вокруг этого правила не ходит столько споров и противоречий.

Все просто зазубрили правило и не делят на ноль, не подозревая, что ответ кроется на поверхности. Сложение, умножение, деление и вычитание — неравноправны, полноценны из перечисленного только умножение и сложение, а все остальные манипуляции с числами строятся из них. То есть запись 10: 2 является сокращением уравнения 2 * х = 10. Значит, запись 10: 0 такое же сокращение от 0 * х = 10. Получается, что деление на ноль — это задание найти число, умножая которое на 0, получится 10. А мы уже разобрались, что такого числа не существует, значит, у этого уравнения нет решения, и оно будет априори неверным.

Рассмотрим пример умножения на ноль целого числа. Сколько будет, если 2 (два) умножить на 0 (ноль)? Любое число, умноженное на ноль, равняется нулю

И не важно, известно нам это число, или не известно

Согласно общепринятому определению, ноль — это число, отделяющее положительные числа от отрицательных на числовой прямой. Ноль — это самое проблематичное место в математике, которое не подчиняется логике, а все математические действия с нулём основаны не на логике, а на общепринятых определениях.

Ноль является первой цифрой во всех стандартных системах счисления. С нулевого дня в календаре майя начинался каждый месяц. Интересно, что тем же самым знаком ноль математики майя обозначали и бесконечность — вторую проблему современной математики. Ноль без палочки. Абсолютный нуль. Ноль целых пять десятых. Пять умножить на ноль — равняется нулю 5 х 0 = 0 Правило умножения на ноль смотрите выше по тексту. Чатыри умножить на ноль бесплатно — бесплатно отвечаю, что будет ноль. В нагрузку бесплатная справка — слово «четыре» пишется чуть-чуть иначе, чем пишите вы в своем поисковом запросе.

https://www.youtube.com/watch?v=EGpr23Tc8iY

Деление на ноль и высшая математика

Школьная арифметика основывалась преимущественно на проведении математических операций с вещественными числами. Большая их часть имеет целый ряд аксиом:

• коммутативность и ассоциативность сложения и умножения;
• существование 0 и 1;
• существование обратного и противоположного элементов.

Кроме этого для вычисления их свойств применяют еще 2 аксиомы – порядка и непрерывности. Так как деление – это процедура противоположная умножению, то при ее проведении возникает 2 проблемы.

Проблема первая – если провести деление на 0, то полученный результат не будет возможности проверить при помощи умножения. Каким бы числом не выступало частное, если его умножить на 0, то делимое все-равно не выйдет получить.

Проблема вторая – если разделить 0 на 0, в итого ответом может выступать любая цифра, которая в случае перемножения с делителем станет нулем.

Все это стало причиной табу в школьной программе на такую операцию, как деление на 0. Но в высшей математике есть возможность его обойти. Например, если построить другую алгебраическую структуру, которая будет отличаться от привычной нам числовой прямой. Примером может служить колесо. У него иные правила и законы. Одним из них является следующий – деление никаким образом не привязано к умножению и трансформируется из бинарной операции в унарную.

Делить на 0 в высшей математике можно, но для этого потребуется выйти за рамки привычного представления о законах и операциях в алгебре.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Вычитание. Что такое уменьшаемое, вычитаемое и разность?

Понятие вычитания лучше всего рассмотреть на примере. Вы решили попить чай с конфетами. В вазе лежало 10 конфет.  Вы съели 3 конфеты. Сколько конфет осталось в вазе? Если мы от 10 вычтем 3 то, в вазе останется 7 конфет. Запишем задачу математически:

10 — 3 = 7

Подробно разберем запись:
10 – это число от которого мы отнимаем или которое уменьшаем, поэтому его называют уменьшаемым.
3 – это число, которое мы вычитаем. Поэтому его называют вычитаемым.
7 – это число результат вычитания или еще его называют разностью. Разность показывает на сколько первое число (10) больше второго числа (3) или насколько второе число (3) меньше первого числа (10).

Если вы сомневаетесь правильно ли нашли разность, нужно сделать проверку. К разности прибавить второе число: 7+3=10

При вычитании натуральных чисел уменьшаемое не может быть меньше вычитаемого.

Делаем вывод из сказанного. Вычитание – это действие, с помощью которого по сумме и одному из слагаемых находится второе слагаемое.

В буквенном виде это выражение будет выглядеть так:

a — b = c

a – уменьшаемое,
b – вычитаемое,
c – разность.

Законы умножения

Некоторые из законов математики мы рассматривали в уроке законы математики. Но мы рассмотрели не все законы. В математике немало законов и разумнее будет изучать их последовательно по мере необходимости.

Для начала вспомним из чего состоит умножение. Умножение состоит из трёх параметров: множимого, множителя и произведения. Например, в выражении 3 × 2 = 6, число 3 — это множимое, число 2 — множитель, число 6 — произведение.

Множимое показывает, что именно мы увеличиваем. В нашем примере мы увеличиваем число 3.

Множитель показывает во сколько раз нужно увеличить множимое. В нашем примере множитель это число 2. Этот множитель показывает во сколько раз нужно увеличить множимое 3. То есть в ходе операции умножения число 3 будет увеличено в два раза.

Произведение это собственно результат операции умножения. В нашем примере произведение это число 6. Это произведение является результатом умножения 3 на 2.

Выражение 3 × 2 также можно понимать, как сумму двух троек. Множитель 2 в таком случае будет показывать сколько раз нужно повторить число 3:

Таким образом, если число 3 повторить два раза подряд, получится число 6.

Переместительный закон умножения

Множимое и множитель называют одним общим словом – сомножители. Переместительный закон умножения выглядит следующим образом:

От перестановки мест сомножителей произведение не меняется.

Проверим так ли это. Умножим к примеру 3 на 5. Здесь 3 и 5 это сомножители.

3 × 5 = 15

Теперь поменяем местами сомножители:

5 × 3 = 15

В обоих случаях мы получаем ответ 15, поэтому между выражениями 3 × 5 и 5 × 3 можно поставить знак равенства, поскольку они равны одному тому же значению:

3 × 5 = 5 × 3

15 = 15

А с помощью  переменных переместительный закон умножения можно записать так:

a × b = b × a

где a и b — сомножители

Сочетательный закон умножения

Этот закон говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.

К примеру, выражение 3 × 2 × 4 состоит из нескольких сомножителей. Чтобы его вычислить, можно перемножить 3 и 2, затем полученное произведение умножить на оставшееся число 4. Выглядеть это будет так:

3 × 2 × 4 = (3 × 2) × 4 = 6 × 4 = 24

Это был первый вариант решения. Второй вариант состоит в том, чтобы перемножить 2 и 4, затем полученное произведение умножить на оставшееся число 3. Выглядеть это будет так:

3 × 2 × 4 = 3 × (2 × 4) = 3 × 8 = 24

В обоих случаях мы получаем ответ 24. Поэтому между выражениями (3 × 2) × 4 и 3 × (2 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:

(3 × 2) × 4 = 3 × (2 × 4)

24 = 24

а с помощью переменных сочетательный закон умножения можно записать так:

a × b × c = (a × b) × c = a × (b × c)

где вместо a, b, c могут стоять любые числа.

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число. Для этого каждое слагаемое этой суммы умножается на это число, затем полученные результаты складывают.

Например, найдём значение выражения (2 + 3) × 5

Выражение находящееся в скобках является суммой. Эту сумму нужно умножить на число 5. Для этого каждое слагаемое этой суммы, то есть числа 2 и 3 нужно умножить на число 5, затем полученные результаты сложить:

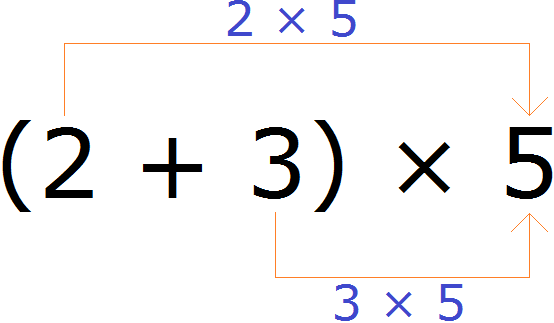
(2 + 3) × 5 = 2 × 5 + 3 × 5 = 10 + 15 = 25

Значит значение выражения (2 + 3) × 5 равно 25.

С помощью переменных распределительный закон умножения записывается так:

(a + b) × c = a × c + b × c

где вместо a, b, c могут стоять любые числа.

Закон умножения на ноль

Этот закон говорит о том, что если в любом умножении имеется хотя бы один ноль, то в ответе получится ноль.

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

Например, выражение 0 × 2 равно нулю

0 × 2 = 0

В данном случае число 2 является множителем и показывает во сколько раз нужно увеличить множимое. То есть во сколько раз увеличить ноль. Буквально это выражение читается так: «увеличить ноль в два раза». Но как можно увеличить ноль в два раза, если это ноль? Ответ — никак.

Иными словами, если «ничего» увеличить в два раза или даже в миллион раз, всё равно получится «ничего».

И если в выражении 0 × 2 поменять местами сомножители, опять же получится ноль. Это мы знаем из предыдущего переместительного закона:

0 × 2 = 2 × 0

0 = 0

Примеры применения закона умножения на ноль:

5 × 0 = 0

5 × 5 × 5 × 0 = 0

2 × 5  × 0 × 9  × 1 = 0

В последних двух примерах имеется несколько сомножителей. Увидев в них ноль, мы сразу в ответе поставили ноль, применив закон умножения на ноль.

Мы рассмотрели основные законы умножения. Теперь рассмотрим самó умножение целых чисел.

Формы записи и терминология

Умножение записывается с использованием знака умножения (∙, ×, *) между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак умножения является бинарным оператором. Знак умножения не имеет специального названия, тогда как, например, знак сложения называется «плюс».

Самый старый из используемых символов — диагональный крестик (×). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
Немецкий математик Лейбниц предпочитал знак в виде приподнятой точки (∙). Этот символ он использовал в письме 1698 года.
Йоханн Ран ввёл звёздочку (∗) в качестве знака умножения, она появилась в его книге «Teutsche Algebra» 1659 г.

В российских учебниках математики в основном используется знак в виде приподнятой точки (∙). Звёздочка (∗) используется, как правило, в текстах компьютерных программ.

Результат записывается с использованием знака равенства «={\displaystyle =}», например:

a⋅b=c{\displaystyle a\cdot b=c}

6⋅3=18{\displaystyle 6\cdot 3=18} («шесть умножить на три равно восемнадцать» или «шестью три равно восемнадцать»).

Часто в математических выражениях знак умножения опускается, если это не вызывает неоднозначного прочтения. Например вместо y=6⋅x+3⋅z{\displaystyle y=6\cdot x+3\cdot z} пишется y=6x+3z{\displaystyle y=6x+3z}. Как правило, знак умножения опускают, если одним из сомножителей является переменная, функция или вложенное выражение в скобках: b2−4ac{\displaystyle b^{2}-4ac}, nsin⁡x{\displaystyle n\sin x}, a(b+c){\displaystyle a(b+c)}.

Ход урока

I. Орг.момент:

Проверка домашнего задания.

II. Устный счет.

Учитель: вспоминаем табличное умножение и деление. Сейчас мы поиграем в игру “Почтальоны”. Света, ты будешь почтальоном. На доске домики с номерами. Твоя задача – взять пример-письмо, правильно его решить и определить в какой дом нам нужно отнести письмо.

3х4 2х2 9х2 3х1 3х8 25:5

6х2 16:4 3х6 9:3 6х4 5:1

4:1 3:1

Учитель: вставьте пропущенный знак действия.

4…0=4 1…3=4 5…1=6

4…4=0 1…3=3 5…1=5

3…3=0 1…0=1 9…0=0

III. Знакомство с новым материалом

ПРО НОЛЬ

Напрасно думают, что ноль

Играет маленькую роль,

Когда-то многие считали

Что ноль не значит ничего

И, как ни странно полагали

Что он совсем не есть число.

Но о его особых свойствах

Мы поведем теперь рассказ

Коль ноль к числу ты прибавляешь

Иль отнимаешь от него

В ответе тотчас получаешь

Опять то самое число

Попав как множитель средь чисел

Он мигом сводит все на нет

И потому в произведенье

Один за всех несет ответ

А относительно деленья

Нам твердо помнить нужно то,

Что уж давно в научно мире

Делить на ноль запрещено

И впрямь: какое из известных

Число за частное нам взять

Когда с нулем в произведенье

Все числа ноль лишь могут дать

Учитель: Давай проверим,все ли в стихотворении правильно:

7+0=7 7-0=7 7•0=0 7:0

Учитель: применим переместительное свойство умножения и заменим умножение сложением: 7•0=0•7=0+0+0+0+0+0+0=0

Что получилось?

Учитель: мы знаем, что деление проверяется умножением: тогда частное умножим на 0 – должно получиться 7, но это не возможно! Какое бы число мы не умножали на 0, всегда в произведении будет 0.

IV. Физминутка

V. Закрепление изученного материала

1. Решение задачи (с. 143 № 7)

Учитель: о чем говорится в задаче?

Ученик: о ремонте, фундаменте, кирпичах.

Учитель: что нужно узнать?

Ученик: сколько кирпичей осталось уложить.

Учитель: сможем ли мы сразу ответить на этот вопрос?

Ученик: нет.

Учитель: почему?

Ученик: потому что мы не знаем, сколько кирпичей рабочий использовал.

Учитель: сможем ли мы это узнать?

Ученик: да.

Учитель: каким действием?

Ученик: делением.

Учитель: сможем ли мы теперь ответить на вопрос задачи?

Ученик: да.

Учитель: каким действием?

Ученик: вычитанием.

Учитель: сколько же кирпичей осталось уложить рабочему?

Ученик: (40:5=8, 40-8=32) 32 кирпича.

2. Самостоятельная работа (с. 144 № 18)

7*0 7:1 3*0 8:1

7*1 0*7 0*3 0:8

1*6 0*1 3*1 0*8

0*6 0:1 1*3 0*1

3. Работа у доски (с. 144 № 11)

7*0 0*8 0:5 1*3 5+0

7+1 0:8 6*0 1+3 5*0

7-1 8+0 8-0 4-1 5-1

VI. Повторение

1. Круговые примеры

Учитель: Мы будем лесниками. Нам надо определить высоту некоторых деревьев, для этого необходимо решить круговые примеры.

2. Арифметический диктант

Учитель: А сейчас будем стенографистами. Я диктую, а ты записываешь – стенографируешь с помощью карточек.

• Сумму чисел 45 и18 (45+18=63)

• Произведение чисел 8 и 3 (8*3=24)

• Разность чисел 35 и 7 (35-7=22)

• Частное чисел 20 и 4 (20:4=5)

3. Геометрический материал.

Учитель: последнее задание. Какие геометрические фигуры вы видите?

Посчитайте и скажите, сколько раз встречается каждая фигура.

(Круг – 12, квадрат – 6, треугольник – 6, прямоугольник – 5.)

VII. Рефлексия

Самостоятельное выполнение с. 144 № 17 (1,2 ст.).Ответы записаны на доске:0,0,0;5,5,5.

Оцени свою работу на уроке смайликом.

VIII. Домашнее задание

С. 144 № 12.

Законы деления

Прежде чем делить целые числа, необходимо изучить два закона деления.

В первую очередь, вспомним из чего состоит деление. Деление состоит из трёх параметров: делимого, делителя и частного. Например, в выражении 8 : 2 = 4,  8 – это делимое, 2 – делитель, 4 – частное.

Делимое показывает, что именно мы делим. В нашем примере мы делим число 8.

Делитель показывает на сколько частей нужно разделить делимое. В нашем примере делитель это число 2. Этот делитель показывает на сколько частей нужно разделить делимое 8. То есть в ходе операции деления, число 8 будет разделено на две части.

Частное – это собственно результат операции деления. В нашем примере частное это число 4. Это частное является результатом деления 8 на 2.

Далее рассмотрим законы деления.

На ноль делить нельзя

Любое число запрещено делить на ноль.

Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если к примеру, у нас имеется два яблока и мы захотим увеличить их в пять раз, то мы запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то мы запишем 10 : 5 = 2

Точно так же можно поступать и с другими выражениями. Если к примеру, 2 × 6 = 12, то мы можем обратно вернуться к изначальному числу 2. Для этого достаточно записать выражение 2 × 6 = 12 в обратном порядке, разделяя 12 на 6

12 : 6 = 2

Теперь рассмотрим выражение 5 × 0. Мы знаем из законов умножения, что произведение равно нулю, если хотя бы один из сомножителей равен нулю. Значит и выражение 5 × 0 равно нулю

5 × 0 = 0

Если записать это выражение в обратном порядке, то получим:

0 : 0 = 5

Сразу в глаза бросается ответ 5, который получается в результате деления ноль на ноль. Это невозможно.

В обратном порядке можно записать и другое похожее выражение, например 2 × 0 = 0

0 : 0 = 2

В первом случае, разделив ноль на ноль мы получили 5, а во втором случае 2. То есть каждый раз деля ноль на ноль, мы можем получить разные значения, а это недопустимо.

Второе объяснение заключается в том, что разделить делимое на делитель означает найти такое число, которое при умножении на делитель даст делимое.

Например выражение 8 : 2 означает найти такое число, которое при умножении на 2 даст 8

… × 2 = 8

Здесь вместо многоточия должно стоять число, которое при умножении на 2 даст ответ 8. Чтобы найти это число, достаточно записать это выражение в обратном порядке:

8 : 2 = 4

Получили число 4. Запишем его вместо многоточия:

4 × 2 = 8

Теперь представим, что нужно найти значение выражения 5 : 0. В данном случае 5 – это делимое, 0 – делитель. Разделить 5 на 0 означает найти такое число, которое при умножении на 0 даст 5

… × 0 = 5

Здесь вместо многоточия должно стоять число, которое при умножении на 0 даст ответ 5. Но не существует числа, которое при умножении на ноль даёт 5.

Выражение … × 0 = 5 противоречит закону умножения на ноль, который утверждает, что произведение равно нулю, когда хотя бы один из сомножителей равен нулю.

А значит записывать выражение … × 0 = 5 в обратном порядке, деля 5 на 0 нет никакого смысла. Поэтому и говорят, что на ноль делить нельзя.

С помощью переменных данный закон записывается следующим образом:

,  при b ≠ 0

Это выражение можно прочитать так:

Число a можно разделить на число b, при условии, что b не равно нулю.

Свойство частного

Этот закон говорит о том, что если делимое и делитель умножить или разделить на одно и то же число, то частное не изменится.

Например, рассмотрим выражение 12 : 4. Значение этого выражения равно 3

12 : 4 = 3

Попробуем умножить делимое и делитель на одно и то же число, например на число 4. Если верить свойству частного, мы опять должны получить в ответе число 3

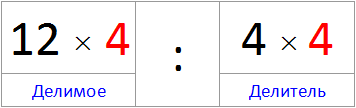
Получили ответ 3.

Теперь попробуем не умножить, а разделить делимое и делитель на число 4

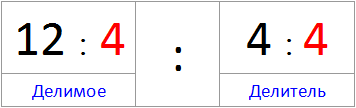
Получили ответ 3.

Видим, что если делимое и делитель умножить или разделить на одно и то же число, то частное не меняется.

Мы рассмотрели два закона деления. Далее рассмотрим деление целых чисел.