Линейные уравнения. решение систем линейных уравнений матричным методом

Способ Крамера

Метод Крамера используют для решения квадратной системы уравнений, представленной в линейном виде, где определитель основной матрицы не равен нулю. Считается, что система обладает единственным решением. Например, задана система линейных уравнений:

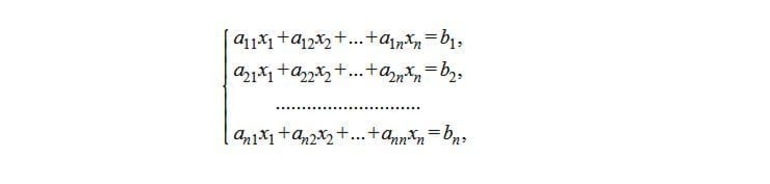
Её необходимо заменить равноценным матричным уравнением.

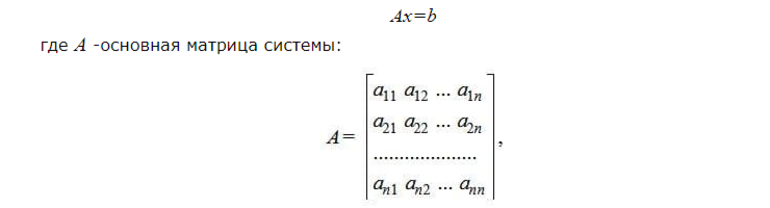
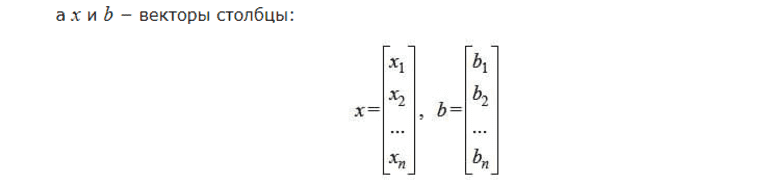
Второй столбец вычисляют, а первый уже задан. Есть предположение, что определитель матрицы отличен от нуля. Из этого можно сделать выводы, что существует обратная матрица. Перемножив эквивалентное матричное уравнение на обратного формата матрицу, получим выражение:

В итоге получают выражения:

Из представленных уравнений выделяют формулы Крамера:

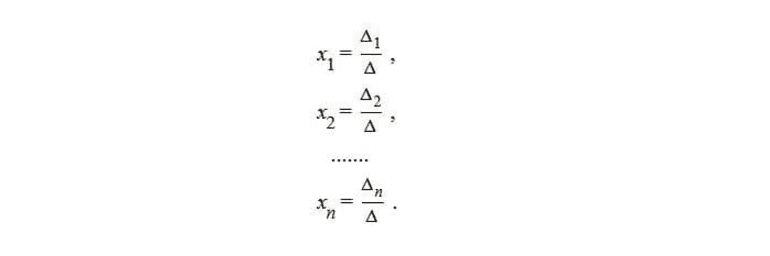
Метод Крамера не представляет сложности. Он может быть описан следующим алгоритмом:

Высчитывают определитель дельта базовой матрицы.
В матричной таблице А замещают первый столбец на вектор свободных элементов b.
Выполняют расчёт определителя дельта1 выявленной матрицы А1.
Определяют переменную Х1 = дельта1/дельта.
Повторяют шаги со 2 по 4 пункт в матрице А для столбов 2,3…n.

Проверить решение матрицы методом Крамера онлайн позволяет калькулятор автоматического расчёта. Для получения быстрого ответа в представленные поля подставляют переменные числа и их количество. Дополнительно может потребоваться указание вычислительного метода разложения по строке или столбу. Другой вариант заключается в приведении к треугольному виду.

Указывается также представление чисел в виде целого числа, обыкновенной или десятичной дроби. После введения всех предусмотренных параметров и нажатия кнопки «Вычислить» получают готовое решение.

Предыдущая
АлгебраЧетность и нечетность функции как определить, примеры решения задач на исследование функции на определение четности и нечетности, условие
Следующая
АлгебраФункция y=k/х свойства и график, область определения функции, коэффициент в графике функции, примеры решения задач

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Что такое матрица распределения ответственности или RACI матрица?

RACI матрица – простой и удобный инструмент для наглядного отображения распределения полномочий и ответственности в рамках проекта или бизнес-процесса. Чаще всего RACI матрица представляет собой табличку, где по вертикали расположены задачи или конкретные результаты, ожидаемые в ходе проекта, а по горизонтали – конкретные люди или роли (роли, конечно, предпочтительнее).

Расшифровка RACI:

1. R (Responsible) – тот, кто будет делать работу. Например, модуль Х будет писать разработчик Вася. Для каждой задачи должен быть как минимум один “R”, можно больше.
2. A (Accountable) – тот, кто примет итоговую работу и будет нести за нее ответственность. Принимать у Васи модуль Х и отвечать перед руководителем проекта головой за то, что он заработает, будет его тимлид Петя. “А” для каждой задачи должен быть только один, отсутствовать “А”, также как и “R”, в задаче не может. В исключительных случаях (обычно для совсем маленьких команд) “А” и “R” будут одним и тем же человеком, тогда достаточно указать просто “А”. Но вообще это нехорошая практика.
3. C (Consulted) – тот, кто будет в обязательном порядке консультировать остальных при выполнении задачи. Чтобы модуль Х работал как надо, и Васе и Пете надо будет согласовать свои идеи по реализации с Инной, главной за информационную безопасность в компании, и Еленой, архитектором проекта. “C” в задаче может быть, а может и не быть.
4. I (Informed) – тот, кто должен быть в курсе принимаемых решений или хода выполнения задачи, но влиять на них никак не будет. Руководитель поддержки Иван, которого пользователи уже запинали в ожидании модуля Х, будет грустно читать статусы и рассылки о ходе разработки модуля, смотреть таски в JIRA и тяжело вздыхать. По аналогии с “C”, “I” в задаче может быть, а может и не быть.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами. На рисунке представлен метод решения:

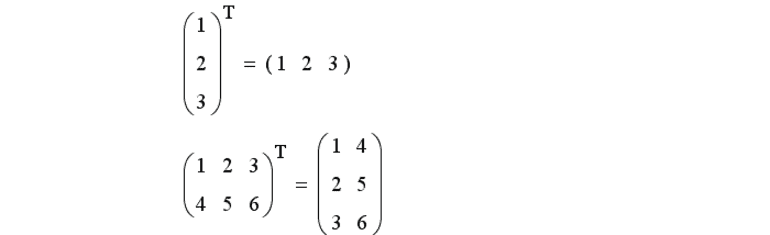
По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2. На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках.

При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

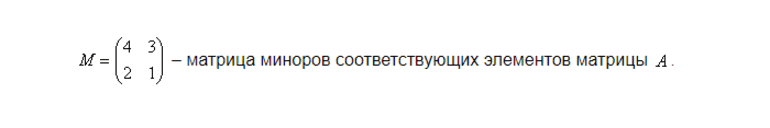
3 этап: находят алгебраические дополнения.

4 этап: определяют транспонированную матрицу.

Итогом будет:

Проверка решения: чтобы удостовериться, что обратная таблица чисел найдена верно, следует выполнить проверочную операцию.

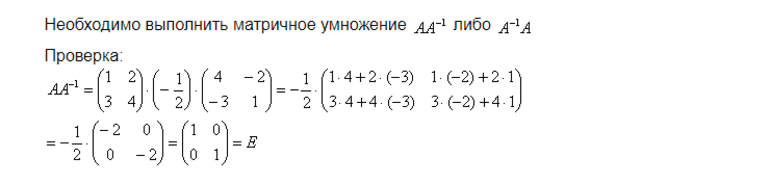
Статистические методы оценки инвестиционных проектов

В
основе процесса принятия управленческих
решений инвестиционного характера
лежат оценка и сравнение объема
предполагаемых инвестиций и будущих
денежных поступлений. Поскольку
сравниваемые показатели относятся к
различным моментам времени, ключевой
проблемой здесь является проблема их
сопоставимости. Воспринимать ее можно
по-разному в зависимости от существующих
объективных и субъективных условий:
темпа инфляции, размера инвестиций и
генерируемых поступлений, горизонта
прогнозирования, уровня квалификации
аналитика и т.п.

Методы,
используемые в анализе инвестиционной
деятельности, можно подразделить на
две группы:

1. основанные
   на учетных оценках («статистические»
   методы):

• срок
  окупаемости инвестиций – PP
  (Payback Period);

• коэффициент
  эффективности (рентабельности) инвестиций
  – ARR
  (Accounted Rate of Return).

1.  основанные
   на дисконтированных оценках («динамические»
   методы):

• чистая
  приведенная стоимость – NPV
  (Net Present Value);

• внутренняя
  норма прибыли – IRR
  (Internal Rate of Return);

• индекс
  рентабельности инвестиций – PI
  (Profitability
  Index);

• модифицированная
  внутренняя норма прибыли – MIRR
  (Modified Internal Rate of Return);

• дисконтированный
  срок окупаемости инвестиций – DPP
  (Discounted Payback Period).

Инвестиционные
проекты, анализируемые в процессе
составления бюджета капитальных
вложений, имеют определенную логику.

С
каждым инвестиционным проектом принято
связывать денежный поток (Cash Flow), элементы
которого представляют собой либо чистые
оттоки (Net Cash Outflow), либо чистые притоки
денежных средств (Net Cash Inflow). Под чистым
оттоком понимается превышение текущих
денежных расходов по проекту над
текущими денежными поступлениями (при
обратном соотношении имеет место чистый
приток). Денежный поток, в котором
притоки следуют за оттоками, называется
ординарным.
Если притоки и оттоки чередуются,
денежный поток называется неординарным.

• Чаще
  всего анализ ведется по годам, хотя это
  ограничение не является обязательным.
  Анализ можно проводить по равным
  периодам любой продолжительности
  (месяц, квартал, год и др.). При этом,
  однако, необходимо помнить о сопоставимости
  величин элементов денежного потока,
  процентной ставки и длины периода.

• Предполагается,
  что все вложения осуществляются в конце
  года, предшествующего первому году
  реализации проекта, хотя в принципе
  они могут осуществляться в течение
  ряда последующих лет.

• Приток
  (отток) денежных средств относится к
  концу очередного года.

• Коэффициент
  дисконтирования, используемый для
  оценки проектов с помощью методов,
  основанных на дисконтированных оценках,
  должен соответствовать длине периода,
  заложенного в основу инвестиционного
  проекта (например, годовая ставка
  берется только в том случае, если длина
  периода – год).

Необходимо
особо подчеркнуть, что применение
методов оценки и анализа проектов
предполагает множественность используемых
прогнозных оценок и расчетов.
Множественность определяется как
возможность применения ряда критериев,
так и безусловной целесообразностью
варьирования основными параметрами.
Это достигается использованием
имитационных моделей в среде электронных
таблиц.

Методы вычисления обратной матрицы

Вычисление обратной матрицы с помощью присоединённой матрицы

Теорема. Если справа к квадратной матрице дописать единичную матрицу того же порядка и с помощью элементарных преобразований над строками преобразовать полученную матрицу так, чтобы начальная матрица стала единичной, то матрица полученная из единичной будет обратной матрицей к исходной.

Замечание. Если при преобразованиях в левой части матрицы образуется нулевая строка (столбец), то исходная матрица не имеет обратной матрицы.

Пример 1. Найти обратную матрицу матрицы A

A =		2	4	1
2	1
2	1	1

Решение: Приписываем к матрице A справа единичную матрицу третьего порядка:

A|E =		2	4	1	1		~
2	1	1
2	1	1	1

Преобразуем левую часть полученной матрицы в единичную. Для этого от 3-тей строки отнимем 1-ую строку:

~		2	4	1	1		~
2	1	1
2 — 2	1 — 4	1 — 1	0 — 1	0 — 0	1 — 0

~		2	4	1	1		~
2	1	1
-3	-1	1

Третью строку поделим на (-3) и поменяем местами со второй строкой:

~		2	4	1	1		~
2	1	1
1	1/3	-1/3

~		2	4	1	1		~
1	1/3	-1/3
2	1	1

Отнимем он 1-ой строки 2-ую умноженную на 4; от 3-тей строки 2-ую умноженную на 2:

~		2 — 4·0	4 — 4·1	1 — 4·0	1 — 4·(1/3)	0 — 4·0	0 — 4·(-1/3)		~
1	1/3	-1/3
0 — 2·0	2 — 2·1	1 — 2·0	0 — 2·1/3	1 — 2·0	0 — 2·(-1/3)

~		2	1	-1/3	4/3		~
1	1/3	-1/3
1	-2/3	1	2/3

Отнимем он 1-ой строки 3-ую строку:

~		2 — 0	0 — 0	1 — 1	-1/3 — (-2/3)	0 — 1	4/3 — 2/3		~
1	1/3	-1/3
1	-2/3	1	2/3

~		2	1/3	-1	2/3		~
1	1/3	-1/3
1	-2/3	1	2/3

Разделим 1-ую строку на 2:

~		1	1/6	-1/2	1/3
1	1/3	-1/3
1	-2/3	1	2/3

Ответ: A-1 =		1/6	-1/2	1/3
1/3	-1/3
-2/3	1	2/3

Вычисление обратной матрицы с помощью союзной матрицы

Определение. Матрица Ã, элементы которой равны алгебраическим дополнениям соответствующих элементов матрицы A называется союзной матрицей.

A-1 =	1	ÃT
det(A)

Пример 1. Найти обратную матрицу матрицы A

A =		2	4	1
2	1
2	1	1

Решение: Найдем определитель матрицы A:

det(A) =	2	4	1	=
2	1
2	1	1

= 2·2·1 + 4·1·2 + 1·0·1 — 1·2·2 — 2·1·1 — 4·0·1 = 4 + 8 + 0 — 4 — 2 — 0 = 6

Найдем алгебраические дополнения матрицы A:

A11 = (-1)1 + 1·	2	1	= 2·1 — 1·1 = 1
1	1

A12 = (-1)1 + 2·	1	= -(0·1 — 1·2) = 2
2	1

A13 = (-1)1 + 3·	2	= 0·1 — 2·2 = -4
2	1

A21 = (-1)2 + 1·	4	1	= -(4·1 — 1·1) = -3
1	1

A22 = (-1)2 + 2·	2	1	= 2·1 — 1·2 = 0
2	1

A23 = (-1)2 + 3·	2	4	= -(2·1 — 4·2) = 6
2	1

A31 = (-1)3 + 1·	4	1	= 4·1 — 1·2 = 2
2	1

A32 = (-1)3 + 2·	2	1	= -(2·1 — 1·0) = -2
1

A33 = (-1)3 + 3·	2	4	= 2·2 — 4·0 = 4
2

Запишем союзную матрицу:

à =		1	2	-4
-3	6
2	-2	4

Найдем обратную матрицу:

A-1 =  1 ÃT  =  1 det(A) 6

1 -3 2 2 -2 -4 6 4

=

1/6 -1/2 1/3 1/3 -1/3 -2/3 1 2/3

Ответ: A-1 =		1/6	-1/2	1/3
1/3	-1/3
-2/3	1	2/3

Матрицы. вступление и оглавлениеМатрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матрицУмножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Ввод данных и функционал

• В качестве элементов используются обыкновенные правильные дроби (, , ), десятичные дроби (, , ), а также числа в экспоненциальной форме (, ).
• Длина вводимых чисел ничем не ограничена, вводите хоть 1000 цифр, правда, возможно, придётся подождать, пока будут идти вычисления!
• Используйте для работы одну или две матрицы (чтобы выполнять операции с двумя матрицами, передвиньте переключатель второй матрицы).
• Вставляйте результат в A или B с помощью кнопок «Вставить в A» и «Вставить в B».
• Перетаскивайте (drag-and-drop) матрицы из результата в A или B.
• Используйте стрелки (, , , ) для перемещения по элементам

Пример

1. Определяем цель составления матрицы приоритетов: уменьшить количество дефектов в изделии.

2. Формируем команду экспертов: для примера состав команды экспертов будет состоять из 3 человек. Каждый из них знаком с методом выработки решений на основе мозгового штурма.

3. Составляем список возможных решений проблемы: список решений поставленной проблемы сформированный командой экспертов.

изменить технологию изготовления;

увеличить число точек контроля;

провести обучение мастеров;

изменить конструкцию изделия;

4. Определяем состав критериев: состав критериев для оценки приоритетности решений.

требуется не более 100 чел\час на реализацию решения

низкая стоимость реализации решения

количество вовлекаемого персонала не более 50 чел.

снижение затрат на брак не менее чем в 1,5 раза.

5. Назначаем весовой коэффициент для каждого критерия. Рассмотри назначение критериев для каждого из 3-х методов — аналитического, метода консенсуса и матричного метода.

Для аналитического метода:

	Критерий	Весовой коэффициент
требуется не более 100 чел\час на реализацию решения	3
низкая стоимость реализации решения	9
количество вовлекаемого персонала не более 50 чел.	1
снижение затрат на брак не менее чем в 1,5 раза	9

Для метода консенсуса:

Устанавливаем, что каждый эксперт может распределить между критериями 4 балла.

Критерий	Эксперт 1	Эксперт 2	Эксперт 3	Весовой коэффициент
требуется не более 100 чел\час на реализацию решения	1	1
низкая стоимость реализации решения	2	3	1	6
количество вовлекаемого персонала не более 50 чел.	1	1
снижение затрат на брак не менее чем в 1,5 раза	1	3	4

Для матричного метода:

Критерии	требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза	Итого
требуется не более 100 чел\час на реализацию решения	Х	1	1
низкая стоимость реализации решения	2	Х	2	1	5
количество вовлекаемого персонала не более 50 чел.	1	Х	1
снижение затрат на брак не менее чем в 1,5 раза	2	1	2	Х	5

6. Определяем наиболее значимые критерии: т.к. количество выбранных для примера критериев составляет всего 4, то оставляем все критерии.

7. Выбираем метод подсчета значимости каждого из предложенных ранее (на шаге 3) решений. Для определения значимости воспользуемся шкалой «1»-«3»-«9», где 9 — наиболее значимое решение, 3 — значимое решение, 1 — малозначимое решение.

8. Проведем оценку значимости кадого решения по отношению к каждому критерию: для оценки значимости решений воспользуемся аналитическим методом. Весовые коэффициенты критериев определены на шаге 5.

Решения	Критерии
требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза
весовой коэффициент =3	весовой коэффициент =9	весовой коэффициент =1	весовой коэффициент =9
изменить технологию изготовления	3	1	1	9
увеличить число точек контроля	9	3	9	3
провести обучение мастеров	9	9	1	1
изменить конструкцию изделия	3	3	9	3

9. Определяем приоритетность каждого решения: оценка каждого решения перемножается на весовой коэффициент каждого критерия и значения суммируются.

Решения	Критерии	Итого
требуется не более 100 чел\час на реализацию решения	низкая стоимость реализации решения	количество вовлекаемого персонала не более 50 чел.	снижение затрат на брак не менее чем в 1,5 раза
весовой коэффициент =3	весовой коэффициент =9	весовой коэффициент =1	весовой коэффициент =9
изменить технологию изготовления	9	9	1	81	100
увеличить число точек контроля	27	27	9	27	90
провести обучение мастеров	27	81	1	9	119
изменить конструкцию изделия	9	27	9	27	72

10. Распределяем решения по порядку приоритетности:

1. Провести обучение мастеров — 118

2. Изменить технологию изготовления — 100

3. Увеличить число точек контроля — 90

4. Изменить конструкцию изделия — 72

Матрица приоритетов, по сравнению с другими метода ранжирования, дает возможность более объективно оценить значимость данных и установить величину этой значимости.

Вместе с тем, очевиден и недостаток этого инструмента качества – он достаточно трудоемкий, особенно когда необходимо провести ранжирование большого количества данных по большому количеству критериев.

Нахождение обратной матрицы методом исключения неизвестных Гаусса

Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса —
приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы
получим сдвоенную матрицу .
Умножим обе части этой матрицы на ,
тогда получим

,

но

и .

Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса

1. К матрице A приписать единичную матрицу того же порядка.

2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась
единичная матрица, тогда в правой части на месте
единичной матрицы автоматически получится обратная матрица. Матрица A в левой части
преобразуется в единичную матрицу путём элементарных преобразований матрицы.

2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо
строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен
нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом
случае дальнейшее нахождение обратной матрицы прекращается.

Пример 2. Для матрицы

найти обратную матрицу.

Решение. Составляем сдвоенную матрицу

и будем её преобразовывать, так чтобы в левой части получилась единичная матрица.
Начинаем преобразования.

Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой,
а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим

.

Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим
предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку
на 2 и вычтем из неё третью строку, тогда получим

.

Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её
с третьей строкой. Тогда получим

.

Разделим третью строку на 8, тогда

.

Умножим третью строку на 2 и сложим её со второй строкой. Получается:

.

Переставим местами вторую и третью строку, тогда окончательно получим:

.

Видим, что в левой части получилась единичная матрица, следовательно, в правой части
получилась обратная матрица .
Таким образом:

.

Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:

.

В результате должна получиться обратная матрица.

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Пример 3. Для матрицы

найти обратную матрицу.

Решение. Составляем сдвоенную матрицу

и будем её преобразовывать.

Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй,
а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим

.

Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки
вычитаем вторую, тогда получим

.

Видим, что в третьей строке в левой части все элементы получились равными нулю.
Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Шаг 4. Выбор решения

Затем каждому альтернативному варианту поставьте оценку соответствия критериям и умножьте на вес критерия, суммируйте и запишите в графе «Итог». Тот вариант решения, который, набрал большее количество баллов, будет более подходящим решением.

В общем виде матрица принятия решения выглядит так:

Альтернативные варианты	Критерий 1	Критерий 2	Критерий 3	Критерий 4	Критерий 5	Итог
Вес критерия	1	3	5	4	2
Вариант 1	3 (3×1)	5 (5×3)	4 (4×5)	3 (3×4)	5 (5×2)	60
Вариант 2	2 (2×1)	4 (4×3)	5 (5×5)	2 (2×4)	3 (3×2)	53
Вариант 3	4 (4×1)	3 (3×3)	2 (2×5)	1 (1×4)	5 (5×2)	37
Вариант 4	5 (5×1)	1 (1×3)	4 (4×5)	5 (5×4)	4 (4×2)	56
Вариант 5	3 (3×1)	4 (4×3)	3 (3×5)	4 (4×4)	2 (2×2)	50

Из таблицы мы видим, что вариант 1 набрал наибольшее количество баллов – 60, а вариант 4, набравший 56 баллов, будет запасным.

 Достоинства метода:

• объективность. В процессе анализа и оценки факторов, влияющих на выбор, субъективные ощущения сводятся к минимуму;
• математическая обоснованность и наглядность. Если вы покажете данные своего анализа другому человеку и четко обоснуете их, то вам гораздо легче будет убедить его в правильности принятого решения;
• возможность найти запасной вариант. Если по каким-то причинам реализовать выбранный вариант не получится, у вас будет запасной вариант – тот, который набрал чуть меньше баллов, чем первый.

На эту тему:

Как выйти из зоны комфорта Колесо баланса жизни, как составить и как использовать Решение личных повседневных проблем

Функции принятия управленческого решения в деятельности предпринимателя

Управленческая деятельность любого руководителя строится на нескольких важнейших элементах таких как:

• целеопределение,
• прогнозирование,
• планирование,
• мотивирование,
• организация,
• контроль,
• и многие другие.

Для успешной деятельности они все одинаково равны, однако, наиболее существенным аспектом работы любого руководителя, как считают многие специалисты в области менеджмента, является функция принятия управленческих решений. Отчасти, это связано с тем, что часть своих полномочий руководитель вполне может передать своим подчинённым, в то время как функцию принятия решений делегировать, таким образом, не получиться, т.к. руководитель сразу потеряет контроль, возможность управлять и перестанет быть руководителем в целом.

Решения, которые изо дня в день приходиться принимать руководителю, связаны с самыми различными сферами его деятельности. Зачастую ошибки в этом процессе могут быть безболезненно исправлены, однако иногда могут оказаться фатальными. Эффективная работа руководителя не представляется возможной без умения принимать грамотные решения, однако большинство руководителей приходят к такому умению сквозь долгий путь проб и ошибок. Из вышесказанного можно сделать вывод, что исследования в данной области носят важный, фундаментальный характер.

Замечание 1

Функцию принятия решений очень тяжело стандартизировать и свести к определённому набору алгоритмов. В связи с этим, роль субъективных, психологических факторов в ней крайне велика. В силу таких обстоятельств функция принятия решения является предметом изучения, как теории управления, так и психологии. Именно функция принятия решений заставляет прочувствовать суть управления, заключающуюся не столько в науке, сколько являющейся искусством.

Решение матричного уравнения вида

Алгоритм решения точно такой же с некоторыми содержательными и техническими отличиями:

Пример 5

Решить матричное уравнение, выполнить проверку найденного решения.

Решение: Уравнение имеет готовый вид , что позволяет сразу же заняться «иксом».

Для разрешения уравнения относительно  умножим обе его части на  справа:

При оформлении можно записать и короче: «Решение ищем в виде ».

Матрица «бэ» известна. Берём матрицу  и без комментариев исследуем обратную сторону Луны:

, где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

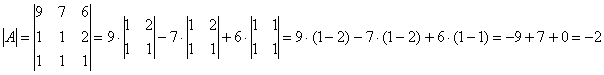
 – матрица миноров соответствующих элементов матрицы .

 – матрица алгебраических дополнений.

 – транспонированная матрица алгебраических дополнений.

Таким образом, обратная матрица:
Находим решение, при этом не забываем про порядок умножения матриц, обратная матрица едет во втором вагоне: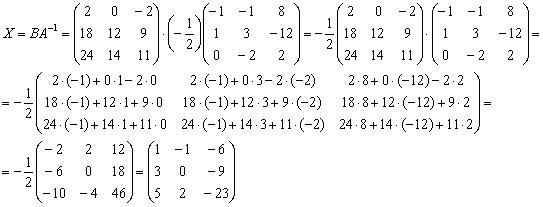

Ответ:

Проверка: Подставим найденное значение  в левую часть исходного уравнения: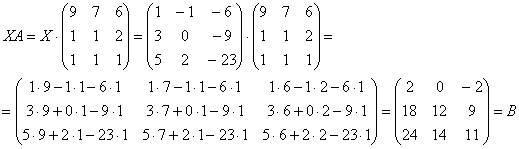

Получена правая часть исходного уравнения. Таким образом, решение найдено правильно.

Усложним задание:

Пример 6

Решить матричное уравнение, сделать проверку: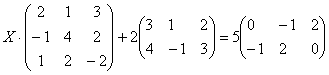

Решение: Незнакомец расположился слева от матрицы, поэтому уравнение сводится к виду . Упаковываем множители, переносим свободную матрицу в правую часть и выполняем вычитание матриц:

Для разрешения уравнения относительно  умножим обе его части на  справа:

Обратную матрицу найдем по формуле:, где  – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .

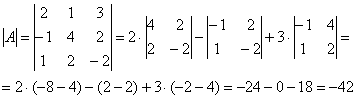
 – матрица миноров соответствующих элементов матрицы .

 – матрица алгебраических дополнений.

 – транспонированная матрица алгебраических дополнений.

Обратная матрица: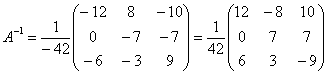

Здесь целесообразно внести минус в матрицу. Возможно, вам надоела однообразная картинка с нахождением обратной матрицы в каждом примере, я бы вполне мог пропускать данный пункт и сразу записывать: «обратная матрица такая-то…». Нет, полное решение приводится не случайно. Это отличная возможность потренироваться! Кроме того, у некоторых студентов действительно очень низкий уровень подготовки и полный трафарет того или иного примера будет как нельзя кстати. Да и сам Гугл, глядишь, научится решать матричные уравнения =)

Находим решение: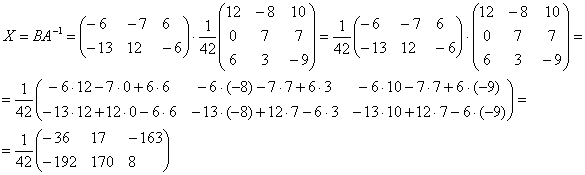

Ответ:

Проверка: Подставим найденное значение  в левую часть исходного уравнения: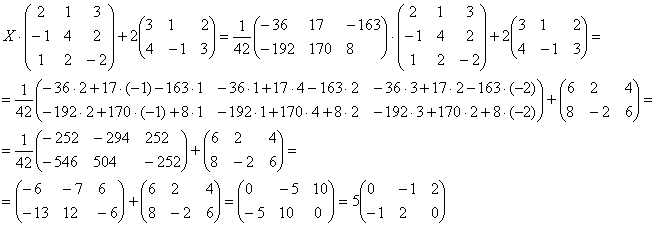
Получена правая часть исходного уравнения, таким образом, решение найдено верно.

Пример 7

Решить матричное уравнение и  сделать проверку: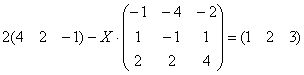

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

В заключение коротко рассмотрим ещё один тип матричного уравнения, который практически не встречается: , где  – известные матрицы. То есть, наш партизан залёг между двумя матрицами.

Разрешим данное уравнение относительно . Сначала умножим обе части на  слева:

Теперь умножим обе части на  справа:

Готового примера у себя в коллекции я не нашёл, но сейчас всё равно что-нибудь подберу из этой оперы….   Вот:

Да, работёнки здесь побольше. Раза в два. Как решить данное уравнение?

– для матрицы   находим обратную матрицу ;
– для матрицы   находим обратную матрицу ;
– перемножаем три матрицы  (см. статью про свойства матричных операций).

Желающие могут прорешать данный пример, верный ответ: .

Поздравляю ещё раз! Если вы читаете эти строки, то Конец Света так и не наступил! Конец Света как деньги – любит тишину =) На самом деле всё было так: летописцы майя составили свой календарь до дня зимнего солнцестояния 2012 года. А потом устали.

Но на всякий случай передаю привет следующей цивилизации. Когда-нибудь они откопают хорошо сохранившийся в вечной мерзлоте сервер и расшифруют нашу клинопись =)

Удачной сдачи зачётов и экзаменов!

Решения и ответы:

(Переход на главную страницу)