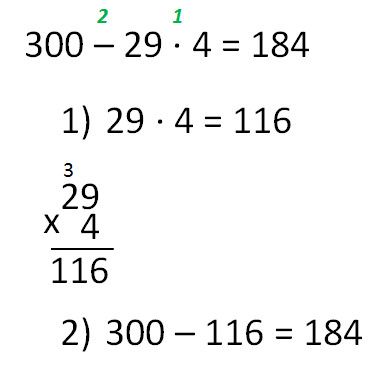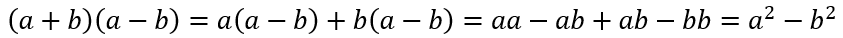Сложение и вычитание степеней

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Как посчитать квадратные метры стены с окном

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Как производится расчет

Рассмотрим расчет на примере даты 18.11.1991 года.

1. Суммируем все цифры даты рождения и получаем первое дополнительное число: 1+8+1+1+1+9+9+1=31
2. Суммируем цифры первого дополнительного числа и получаем второе дополнительное число: 3+1=4
3. Вычитаем из первого дополнительного числа первую цифру числа рождения, умноженную на 2. Получаем третье дополнительное число. 31-(1х2)=29
4. Суммируем цифры третьего дополнительного числа и получаем четвертое дополнительное число. 2+9=11

Делаем таблицу из 2 строк и 8 столбцов. В первую строку вписываем все цифры дня рождения в порядке «число-месяц-год», а во вторую – все дополнительные числа, с первого по четвертое. Если число рождения, месяц или рабочее число – однозначное, то записываем его в две ячейки, причем в первой ставим 0.

1	8	1	1	1	9	9	1
3	1	4	2	9	1	1

Считаем, сколько раз встречается каждая цифра в двух строках, и заполняем квадрат Пифагора.

11111111 характер, сила воли	4 здоровье, красота	— удача, везение
2 энергетика, харизма	— логика, интуиция	8 чувство долга
3 познание, творчество	— трудолюбие, мастерство	999 память, ум

Расчет готов. Переходим к расшифровке.

Квадрат (алгебра) — Википедия

Материал из Википедии — свободной энциклопедии

Квадра́т

Вычисление x2{\displaystyle x^{2}} — математическая операция, называемая возведе́нием в квадра́т. Эта операция представляет собой частный случай возведения в степень, а именно — возведение числа x{\displaystyle x} в степень 2.

Далее приведено начало числовой последовательности для квадратов целых неотрицательных чисел (последовательность A000290 в OEIS):

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, …

Исторически натуральные числа из этой последовательности называли «квадратными».

Квадрат натурального числа n{\displaystyle n} можно представить в виде суммы первых n{\displaystyle n} нечетных чисел:

1: 1=1{\displaystyle 1=1}

2: 4=1+3{\displaystyle 4=1+3}

…

7: 49=1+3+5+7+9+11+13{\displaystyle 49=1+3+5+7+9+11+13}

…

Ещё один способ представления квадрата натурального числа:n2=1+1+2+2+…+(n−1)+(n−1)+n{\displaystyle n^{2}=1+1+2+2+\ldots +(n-1)+(n-1)+n}Пример:

1: 1=1{\displaystyle 1=1}

2: 4=1+1+2{\displaystyle 4=1+1+2}

…

4: 16=1+1+2+2+3+3+4{\displaystyle 16=1+1+2+2+3+3+4}

…

Сумма квадратов первых n{\displaystyle n} натуральных чисел вычисляется по формуле:∑k=1nk2=12+22+32+…+n2=n(n+1)(2n+1)6{\displaystyle \sum _{k=1}^{n}k^{2}=1^{2}+2^{2}+3^{2}+\ldots +n^{2}={\frac {n(n+1)(2n+1)}{6}}}

Вывод

Способ 1, метод приведения:

Рассмотрим сумму кубов натуральных чисел от 1 до n+1{\displaystyle n+1}:

∑k=1nk3+(n+1)3=∑k=0n(k+1)3=∑k=0n(k3+3k2+3k+1)=∑k=0nk3+∑k=0n3k2+∑k=0n3k+∑k=0n1=∑k=0nk3+3∑k=0nk2+3∑k=0nk+∑k=0n1{\displaystyle \sum _{k=1}^{n}k^{3}+(n+1)^{3}=\sum _{k=0}^{n}(k+1)^{3}=\sum _{k=0}^{n}(k^{3}+3k^{2}+3k+1)=\sum _{k=0}^{n}k^{3}+\sum _{k=0}^{n}3k^{2}+\sum _{k=0}^{n}3k+\sum _{k=0}^{n}1=\sum _{k=0}^{n}k^{3}+3\sum _{k=0}^{n}k^{2}+3\sum _{k=0}^{n}k+\sum _{k=0}^{n}1}

Получим:

(n+1)3=3∑k=0nk2+3∑k=0nk+∑k=0n1=3∑k=0nk2+3(n+1)n2+(n+1){\displaystyle (n+1)^{3}=3\sum _{k=0}^{n}k^{2}+3\sum _{k=0}^{n}k+\sum _{k=0}^{n}1=3\sum _{k=0}^{n}k^{2}+3{\frac {(n+1)n}{2}}+(n+1)}

Умножим на 2 и перегруппируем:

6∑k=0nk2=2(n+1)3−3(n+1)n−2(n+1)=(n+1)(2(n+1)2−3n−2)=(n+1)(2n2+n)=n(n+1)(2n+1){\displaystyle 6\sum _{k=0}^{n}k^{2}=2(n+1)^{3}-3(n+1)n-2(n+1)=(n+1)(2(n+1)^{2}-3n-2)=(n+1)(2n^{2}+n)=n(n+1)(2n+1)}

∑k=0nk2=n(n+1)(2n+1)6{\displaystyle \sum _{k=0}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}}       (В рассуждениях использована формула: ∑k=0nk=(n+1)n2{\displaystyle \sum _{k=0}^{n}k={\frac {(n+1)n}{2}}}, вывод которой аналогичен приведенному)

Способ 2, метод неизвестных коэффициентов:

Заметим, что сумма функций степени N{\displaystyle N} может быть выражена как функция N+1{\displaystyle N+1} степени. Исходя из этого факта предположим:

∑k=0nk2=f(n)=An3+Bn2+Cn+D{\displaystyle \sum _{k=0}^{n}k^{2}=f(n)=An^{3}+Bn^{2}+Cn+D}

f(0)=0;f(1)=1;f(2)=5;f(3)=14{\displaystyle f(0)=0;f(1)=1;f(2)=5;f(3)=14}

Получим систему линейных уравнений относительно искомых коэффициентов:

{0A+0B+0C+D=0A+B+C+D=18A+4B+2C+D=527A+9B+3C+D=14{\displaystyle {\begin{cases}0A+0B+0C+D=0\\A+B+C+D=1\\8A+4B+2C+D=5\\27A+9B+3C+D=14\\\end{cases}}}

Решив её, получим A=13,B=12,C=16,D=0{\displaystyle A={\frac {1}{3}},B={\frac {1}{2}},C={\frac {1}{6}},D=0}

Таким образом:

∑k=0nk2=f(n)=13n3+12n2+16n+0=n(n+1)(2n+1)6{\displaystyle \sum _{k=0}^{n}k^{2}=f(n)={\frac {1}{3}}n^{3}+{\frac {1}{2}}n^{2}+{\frac {1}{6}}n+0={\frac {n(n+1)(2n+1)}{6}}}

Квадрат комплексного числа в алгебраической форме можно вычислить по формуле:

(a+bi)2=(a2−b2)+2abi.{\displaystyle \left(a+bi\right)^{2}=\left(a^{2}-b^{2}\right)+2abi.}

Аналогичная формула для комплексного числа в тригонометрической форме:

(r(cos⁡ϕ+isin⁡ϕ))2=r2(cos⁡2ϕ+isin⁡2ϕ).{\displaystyle \left(r\left(\cos \phi +i\sin \phi \right)\right)^{2}=r^{2}\left(\cos {2\phi }+i\sin {2\phi }\right).}

Квадрат числа равен площади квадрата со стороной, равной этому числу.

Грэхем Р., Кнут Д., Паташник О. — Конкретная математика. Основание информатики. Пер. с англ. —М.: Мир, 1998. —703 с.

Примеры

Последовательность квадратов начинается так:

0, 1, , , , , , , , , , , , , , , , , , , , , , , , , , , 784, 841, 900, 961, , , 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, … (последовательность A000290 в OEIS)

Таблица квадратов

	_0	_1	_2	_3	_4	_5	_6	_7	_8	_9
0_	1	4	9	16	25	36	49	64	81
1_	100	121	144	169	196	225	256	289	324	361
2_	400	441	484	529	576	625	676	729	784	841
3_	900	961	1024	1089	1156	1225	1296	1369	1444	1521
4_	1600	1681	1764	1849	1936	2025	2116	2209	2304	2401
5_	2500	2601	2704	2809	2916	3025	3136	3249	3364	3481
6_	3600	3721	3844	3969	4096	4225	4356	4489	4624	4761
7_	4900	5041	5184	5329	5476	5625	5776	5929	6084	6241
8_	6400	6561	6724	6889	7056	7225	7396	7569	7744	7921
9_	8100	8281	8464	8649	8836	9025	9216	9409	9604	9801

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 51 человек(а). Количество просмотров этой статьи: 653 660.

Категории: Математика

English:Calculate a Square Root by Hand

Italiano:Calcolare la Radice Quadrata a Mano

Español:calcular una raíz cuadrada

Deutsch:Die Quadratwurzel von Hand berechnen

Português:Calcular uma Raiz Quadrada à Mão

Français:calculer une racine carrée à la main

中文:手算平方根

Nederlands:De wortel van een getal uitrekenen zonder rekenmachine

Bahasa Indonesia:Menghitung Akar Kuadrat Secara Manual

Čeština:Jak vypočítat odmocninu bez kalkulačky

ไทย:คำนวณหารากที่สองด้วยมือ

Türkçe:Karekök Elle Nasıl Hesaplanır

हिन्दी:हाथों से वर्गमूल की गणना करें

한국어:손으로 루트 값 계산하기

العربية:حساب الجذر التربيعي يدويا

Печать

Как определять точные углы для цены при помощи Квадрата 9 Ганна

Допустим по какому либо вымышленному финансовому инструменту цена равна 14,30$.

Первое, что нам нужно сделать это привести цену к формату чисел не использующих запятую – 14,30$ = 143

Приведение цены к числам без запятой

В данном примере мы переносим запятую на один знак вправо. В итоге получаем число 143.

Отмечаем ячейку с числом 143 на Квадрате 9 Ганна.

Следующий шаг который мы должны сделать, это определить ячейку на диагональном или координальном крестах с числом наиболее близко раположенном к искомому. В данном случае искомое число 145, которое расположено в ячейке на диагональном кресте.

Ищем на крестах ближайшее к искомой цене число

Теперь нам нужно определить цикл в котором находится данная ячейка. Ячейка с числом 143 находится в 6 цикле.

Определяем номер цикла в котором находится наша цена

Это как мы уже знаем означает то, что в данном цикле есть по 6 цифр между каждыми 45 градусами.

Теперь вычисляем размер на который увеличивается число при перемещении на один градус. В дальнейшем будем называть такое перемещение – одноградусной фракцией цикла. Для этого разделим количество ячеек между углами на 45 градусов. 6 делим на 45 и получаем количество одноградусной фракции используемой для этого цикла.

Вычисляем количество одноградусной фракции для цикла 6

Теперь считаем разницу между нашим искомым числом и числом 145 – она равна двум.

Разница между искомым числом и диагональным

Разделим полученный результат на одноградусную фракцию нашего цикла.

Делим разницу на фракцию цикла

Получаем 15 градусов.

Теперь прибавляем это количество градусов к 45, либо отнимаем от 135, в зависимости от того какую точку мы используем для начала отсчёта, то есть слева или справа от оси.

Так как ближайшее число находится именно на этом градусе, 45+15 получается 60. 135-15 получается 120. Точный угол для цены 14,30$ либо 60, либо 120 градусам. Так как вычислять такие углы мы будем часто, а цены могут иметь больше цифр, чем в приведённом нами примере после перемещения запятой. К примеру для пары EUR/USD цена может составлять и пять и шесть цифр, а увеличивать Квадрат девяти не  всегда удобно. Предлагаем заранее подготовить расчеты и записать их в отдельную таблицу. А при необходимости просто использовать готовые данные.

Точка отсчета углов для цены

Как уже было сказано ранее, нет большой разницы какую из трёх предлагаемых Ганном точек для начала отсчета градусов на окружности использовать. Поэтому для будущих своих вычислений определитесь с какой-нибудь одной и постоянно используйте её, чтобы не происходило разного рода путаниц с числовыми обозначениями углов.

Нечетные и четные квадратные числа

Квадраты четных чисел четные (и на самом деле делятся на 4), так как (2 n ) 2 = 4 n 2 .

Квадраты нечетных чисел нечетные, так как (2 n + 1) 2 = 4 ( n 2 + n ) + 1 .

Отсюда следует, что квадратные корни из четных квадратных чисел четны, а квадратные корни из нечетных квадратных чисел нечетны.

Поскольку все четные квадратные числа делятся на 4, четные числа в форме 4 n + 2 не являются квадратными числами.

Поскольку все нечетные квадратные числа имеют форму 4 n + 1 , нечетные числа формы 4 n + 3 не являются квадратными числами.

Квадраты нечетных чисел имеют форму 8 n + 1 , поскольку (2 n + 1) 2 = 4 n ( n + 1) + 1 и n ( n + 1) является четным числом.

Каждый нечетный совершенный квадрат представляет собой восьмиугольное число с центром . Разница между любыми двумя нечетными полными квадратами кратна 8. Разница между 1 и любым большим нечетным совершенным квадратом всегда в восемь раз больше треугольного числа, в то время как разница между 9 и любым большим нечетным полным квадратом в восемь раз больше треугольного числа минус восемь. Поскольку все треугольные числа имеют нечетный множитель, но никакие два значения 2 n не отличаются на величину, содержащую нечетный множитель, единственный полный квадрат формы 2 n — 1 равен 1, а единственный полный квадрат формы 2 n + 1 равно 9.

Обратные операции

Извлечение корня

У возведения в степень две обратные операции. Первая – извлечение корня. Подробнее о корнях в Python вы можете почитать в нашей статье. Отметим лишь, что корень в питоне вычисляется с помощью той же функции pow():

Либо с применением оператора «**»:

Для извлечения квадратного корня справедливы оба вышеуказанных способа, но существует и третий, специализированный. Для его применения требуется импортировать модуль

Логарифмирование

Логарифмирование – вторая обратная операция.

Здесь – логарифм. Пример из математики – найдем значение выражения:

Легче всего эта запись читается в формате вопроса: «В какую степень нужно возвести 2, чтобы получить 16?». Очевидно, в 4-ю. Следовательно,

В питоне операция нахождения логарифма так же заложена в функционал модуля math:

Как в Excel написать число в степени?

Часто вам важно, чтобы число в степени корректно отображалось при распечатывании и красиво выглядело в таблице. Как в Excel написать число в степени? Здесь необходимо использовать вкладку «Формат ячеек»

В нашем примере мы записали цифру «3» в ячейку «А1», которую нужно представить в -2 степени.

Последовательность действий следующая:

1. Правой кнопкой мыши щелкаем по ячейке с числом и выбираем из выскакивающего меню вкладку «Формат ячеек». Если не получилось – находим вкладку «Формат ячеек» в верхней панели или жмем комбинацию клавиш CTRL+1.
2. В появившемся меню выбираем вкладку «Число» и задаем формат для ячейки «Текстовый». Жмем ОК.
3. В ячейке A1 вводим рядом с числом «3» число «-2» и выделяем его.
4. Снова вызываем формат ячеек (например, комбинацией горячих клавиш CTRL+1) и теперь для нас только доступна вкладка «Шрифт», в которой отмечаем галочкой опцию «надстрочный». И жмем ОК.
5. В результате должно отображаться следующее значение:

Пользоваться возможностями Excel просто и удобно. С ними вы экономите время на осуществлении математических подсчетов и поисках необходимых формул.

Форма рассчитываемого помещения

Квадрат и прямоугольник

Это чуть ли не самые встречаемые в строительстве формами комнат. По вышеописанному принципу можно узнать их площади. В том случае, если есть выступы, колонны или другие архитектурные нюансы – нужно их обмерить и перемножить. В результате из общей площади вычитаются результаты замеров строительных элементов. Полученная цифра и является верной величиной.

Помимо часто встречаемых квадратных и прямоугольных комнат существуют еще и помещения «неправильной формы». К ним относятся следующие.

Чтобы рассчитать площадь квадратной комнаты, нужны школьные знания и минимальный набор инструментов.

Трапециевидные

Как считать площадь комнаты трапеции? Для этого нужно измерить две ее параллельные стены и высоту (Н), перпендикулярную им.

Высоту следует измерить в нескольких местах, чтобы убедиться в параллельности стен.

Формула, по которой затем вычисляется площадь трапеции:

S=1/2(A+B)*H

Вам понадобится рулетка, карандаш или ручка и лист бумаги.

С выступом

1. Измерить длину и ширину комнаты без выступа.
2. Измерить длину и ширину самого выступа.
3. Вычислить обе площади и сложить.

В результате получается показатель общей площади.

С нишей

1. Измерить длину и ширину общей площади.
2. Измерить длину и ширину ниши.
3. Рассчитать оба показателя и из общей площади вычесть площадь ниши.

Измерить площадь помещения не так уж и сложно. Главное, придерживаться всех правил.

Круглая

Для того, чтобы рассчитать площадь круга, нужно найти его радиус, высоту, длину хорды. Для расчета значения используется формула: S=n(R*R)/2, где S – площадь, n – число пи (3,14) и R – радиус.

Если у имеющейся квадратуры есть круглые элементы или колонны и их площадь нужно вычесть, при этом нельзя изменить радиус или диаметр, тогда измеряется длина окружности и применяется формула S=(P*P)/4n.

Чтобы рассчитать площадь круглого помещения, нужно найти радиус, высоту и длину хорды.

Полукруглая

Как высчитать квадратные метры комнаты, если она содержит в себе полукруг? Расчеты требуется производить после того, как этот элемент разбит на полукруг и прямоугольник. Посчитать обе площади и сложить сумму.

Части помещения с круглой и полукруглой формой можно измерить гибкой рулеткой или веревкой.

Такие формы жилищ встречаются с арками, эркерами, полукруглыми балконами и т.д.

Круглые или полукруглые формы можно измерить гибкой рулеткой или веревкой.

Чтение по диагонали

В квадрате две диагонали. Одна идет сверху слева вниз направо, вторая справа сверху вниз налево. Им соответствую ячейки 1-5-9 и 3-5-7.

Диагональ 3-5-7 отображает сексуальный темперамент носителя. Чем больше там цифр, тем выше сексуальность.

Однако это не выдает развязный характер хозяина, а просто определяет его темперамент.

Вторая диагональ, 1-5-9, посвящена духовности. Об ее высоком развитии говорит показатель равный 5. Если чисел больше, речь о фанатизме, сектантстве. А вот отсутствие чисел выдает бездуховную натуру.

Теперь толкование квадрата Пифагора можно обратить и на выявление степени близости с избранником. Для этого следует сложить количество чисел по столбцам, строкам и диагонали. Чем меньше расхождение в обоих квадратах, тем гармоничнее будет союз. Но все это не значит, что над своей жизнью уже можно не работать совсем – толкования лишь предупреждают.

Специальная вставка

Степень «Квадрат» при желании можно вставить в качестве отдельного символа, но на деле подобный прием почти не встречается. В Word’е есть функция под названием «Вставка». Если ее правильно использовать, юзер сможет осуществлять грамотное форматирование текстовых документов. И возвести число в степень не составит никакого труда.

В нашем случае необходимо выполнить следующие операции:

1. Зайти в текстовый редактор и установить курсор в месте печати степени.
2. Перейти во вкладку «Вставка». Она располагается на панели инструментов «Ворда» в верхней части строки.
3. Выбрать опцию «Символ».
4. Отыскать цифру 2, смещенную в сторону верхней границы «ячейки». Например, можно без труда обнаружить символ степени «Квадрат» в наборе шрифта Vani.
5. Дважды нажать ЛКМ по миниатюре выбранного символа.
6. Закрыть маленькое диалоговое окно посреди текстового редактора.

Такой расклад позволяет вставить символ «квадрата» в текст, но встречается в реальной жизни он не слишком часто. Связано это с трудностями поиска необходимого знака. Кроме того, юзеры могут воспользоваться более простыми и универсальными приемами.

Степень

Целочисленная

В целочисленную степень можно возводить положительные и отрицательные и числа:

И функция и оператор «**» умеют возводить комплексные числа:

Показатель степени может быть положительным, отрицательным и нулевым:

Результат не определён, когда 0 возводят в отрицательную степень:

Ошибка деления на ноль возникает из-за следующего свойства степени:

Рациональная

Возведение числа в рациональную степень напрямую связано с извлечением корня из этого числа отношением:

Если рациональный показатель отрицательный, а основание равно нулю, то Питон все ещё будет выдавать ошибку:

В случае, когда основание меньше нуля, числитель показателя нечётный, а знаменатель, напротив, чётный, результат получается комплексным. Но это свойство рациональных степеней учитывается только в функции

В остальном возведение в рациональную степень работает, как и для целочисленной:

Вещественная

В начале автор объявил, что возведение в степень – штука несложная. Так вот, для вещественных степеней это уже не совсем так. Идеи, заложенные в эту операцию, хоть и просты, но их много, и каждая из них достойна собственной статьи. Описать вкратце разложение в ряд Тейлора и численное интегрирование не получится. Это будет не справедливо, как по отношению к вам, так и к математике. Поэтому, выделим главное:

Python умеет возводить в вещественную степень даже вещественные числа (пусть и псевдо)

Сделать такое инструментами математики ой как непросто:

Шаблонный калькулятор цены и времени

Квадрат 9 Ганна – шаблонный калькулятор цены и времени

В 1920 году Ганном был создан квадрат девяти (Квадрат Ганна). Это своего рода финансовый калькулятор для исследований и торговли. Квдрат девяти Ганн называл шаблонным калькулятором цены и времени. Квдрат девяти бессомненно является одним из самых популярных и таинственных инструментов рынка. Есть в нём нечто такое, что заинтриговывает абсолютно всех, кто с ним хоть раз сталкивался. Будь то профессионал или начинающий трейдер.

Про методы использования квадрата 9 Ганна написано много всевозможных статей и материалов. Но практически не в одной из этих работ не дано полного объяснения по работе с этим уникадьным инструментом. Каждый кто пытался изучать квадрат 9-ти наверняка задавался вопросом: Что это ? Просто обещание больших заработков для тех кто поймёт секретный код, заложенный в калькуляторе легендарного трейдера? Или это намного больше нежели просто калькулятор – нечто, что откроет путь великого познания окружающей нас действительности, включая финансовые рынки.

Во время знакомства с Квадратом 9-ти, начинаешь понимать, что его использование простирается далеко вне того, что бы быть просто интересным торговым инструментом легендарного предсказателя

Который можно использовать не только в качестве математического, но и что не мало важно, в качестве астрономического калькулятора предсказывающего будущее

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

Схема комнаты с нанесенными измерениями

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

• Считаем большой прямоугольник: 5 м * 4,35 м = 21,75 м².
• Находим квадратуру маленького: 2,5 м * 2,65 м = 6,625 м².
• Площадь пола в этом помещении равна сумме 21,75 м² + 6,625 м² = 28,375 м².

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

• Большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Для простоты округлим до 3,38 м².
• Средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м².  Снова округлим до 0,67 м².
• Самый маленький прямоугольник (в нашем случае это будет квадрат): 0,57 м *0,57 м = 0,3249 м2, после округления имеем 0,33 м².
• Чтобы найти общую площадь складываем квадратуру двух прямоугольников и добавляем половину площади последнего, самого маленького участка. 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

https://youtube.com/watch?v=YL07nZH5ueY

Вычислительные приёмы

На олимпиаде Кенгуру и на Внешнем независимом тестировании запрещено пользоваться калькуляторами

Поэтому очень важно научиться тратить на вычисления как можно меньше времени, чтобы использовать его на обдумывание задач

Умножение двузначного числа на 11

Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.

Примеры: 45х11

Складываем 4+5=9. Поэтому результатом будет 495.

76х11 Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.

Математическое обоснование: Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b

Умножение и деление на 5 и 25

Чтобы число умножить число на 5, его нужно разделить на 2 и умножить на 10. Чтобы число разделить на 5, его нужно умножить на 2 и разделить на 10.

Аналогично, умножение/деление на 25 заменяется делением/умножением на 4 и умножением/делением на 100

Примеры: 36х5

Делим 36 на 2, получаем 18. Умножаем 18 на 10 и получаем 180.

3/5 Умножаем 3 на 2 и получаем 6. Делим 6 на 10 и получаем 0,6

45/25 Умножаем 45 на 4, получаем 180. Делим 180 на 100, получаем 1,8

84х25 Делим 84 на 4, получаем 21. Умножаем 21 на 100 и получаем 2100.

Математическое обоснование: Поскольку 5=10/2, умножение/деление на 2 можно свести к более простым умножениям/делениям на 2 и 10.

Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.

Примеры: 652 Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.

1152 Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.

Математическое обоснование: Возведём в квадрат число 10n+5. (10n+5)2 = 100n2+100n+25 = 100n(n+1)+25, откуда и следует данное правило.

Возведение в квадрат числа, близкого к круглому

Целесообразно воспользоваться формулами квадрата суммы или разности.

Примеры: 192 = (20-1)2 = 400–40+1=361

422 = (40+2)2 = 1600+160+4 = 1764

Математическое обоснование: Формула квадрата суммы: (a+b)2 = a2+2ab+b2 Формула квадрата разности: (a-b)2 = a2–2ab+b2

Вычитание из степени десятки

Для вычитания числа из степени десятки, нужно последнюю его цифру заменить дополнением до десяти, а остальные (включая первые виртуальные нули) – дополнениями до девяти.

Примеры: 1000-725 = (9-7)(9-2)(10-5) = 275

100000 – 1237 = 100000 – 01237 = (9-0)(9-1)(9-2)(9-3)(10-7) = 98763

Математическое обоснование: Правило следует из алгоритма вычитания столбиком.

Прибавление числа, близкого к степени десятки

Вместо прибавления числа, состоящего из девяток и оканчивающегося на 9 (8, 7, 6 и т.д.), прибавьте следующую большую степень десятки и вычтите 1 (2, 3, 4 и.т.д)

Примеры: 125+999 = 1125-1 = 1124

6528+996 =7258-4=7254

Математическое обоснование: Для k-значного числа 99…9 = 100..00 – 1

Упрощённые признаки делимости на 4 и 8

Обычно для проверки делимости на 4 применяется следующий признак: Если двуциферное окончание числа делится на 4, то и само число делится на 4.

Однако, использовав обобщённый признак делимости, заметим, что число 10 даёт остаток 2 при делении на 4. Поэтому переформулируем правило так: Если сумма последней цифры с удвоенной предпоследней делится на 4, то и само число делится на 4.

Аналогично для делимости на 8. Вместо проверки на делимость трёхциферного окончания, можно выполнять проверку суммы последней, удвоенной предпоследней и учетверённой третьей с конца цифры.

Примеры: Число 1324 4+2*2=8 – делится на 4.

4+2*2+3*4=20 – не делится на 8

Число 6328 8+2*2=12 – делится на 4.

8+2*2+3*4=24 – делится на 8

Математическое обоснование: Обобщённый признак делимости подробно рассмотрен в отдельной статье.

Как вычислить квадрат числа ? число в квадрате ? Математика

10 ноября 2011

Автор КакПросто!

«Квадратом» числа обычно называют результат математической операции возведения этого числа во вторую степень, то есть однократного умножения его на само себя. С точки зрения геометрии результат этой операции можно представить как площадь квадрата (геометрической фигуры) со стороной, длина которой равна исходному числу. Очевидно, именно это обстоятельство лежало в основе возникновения такого названия операции возведения во вторую степень.

Инструкция

Введите число, квадрат которого надо вычислить — просто наберите его на клавиатуре или пощелкайте по соответствующим кнопкам интерфейса калькулятора. Затем введите команду умножения — нажмите на клавиатуре клавишу со звездочкой или щелкните по такой же кнопке в интерфейсе. Вводить второй раз число не требуется, просто нажмите клавишу Enter и калькулятор покажет результат умножения числа на само себя.

Совет полезен?