Как сделать деревянные головоломки

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.
В таблице 8х8 эти области включают 4 элемента (2х2).
В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.
В центр второй горизонтальной строчки ставятся цифры 6 и 7.
В четвёртой строке слева пишется 13, а справа — 16.

https://youtube.com/watch?v=gB3IQNdUo-4

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

Предыдущая
МатематикаАлгоритм Евклида — формулы, правила и примеры решения задач
Следующая
МатематикаМинор матрицы — способы, порядок и примеры вычисления

Как рассчитать магический квадрат Пифагора самому?

Пифагор — математик, заложивший основы нумерологии. Ученый верил, что миром правят числа. Даже человеческая сущность зависит от них, ведь дата рождения не что иное, как число.

Магический квадрат Пифагора — фигура третьего порядка, клетки которой заполнены числами от 1 до 9. Он делится на 3 уровня: материальный, души и разума.

Цифры даты рождения вписываются в определенном порядке. Полученная комбинация рассказывает о заложенных природой способностях человека.

Материал может быть использован на занятии математического кружка, на внеклассном мероприятии. Цель — развить и расширить познавательный кругозор и логическое мышление.

Решаем магический квадрат Пифагора: пример

Дата рождения: 17.09.2005 г. Складываем эти цифры, не учитывая нули: 1 + 7 + 9 + 2 + 5 = 24. Аналогично поступаем с цифрами результата: 2 + 4 = 6.

Из первой суммы вычитаем удвоенную первую цифру дня рождения: 24 -2 = 22. Снова складываем: 2 + 2 = 4. Полученные числа: 17; 9; 25; 24; 6; 22; 4.

Цифры вписываем в магический квадрат так, чтобы все единицы оказались в первой клеточке, двойки — во второй и так далее. Нули не учитываем.

Результат:

Значение:

Задачи на составление магических квадратов часто включаются в сборники нестандартных заданий. Они встречаются на олимпиадах. Увлеченным математикой школьникам будет полезно узнать об этом классе задач. 

Об авторе: Филиппова Оксана, учитель математики, физики и информатики.

Есть мнение? Оставьте свой комментарий:

Средний слой

Ставим ребра среднего слоя на свои места.

Кубик следует перевернуть так, чтобы несобранная грань оказалась сверху. Самые крайние детали, выступающие за пределы кубика, нужно держать сверху до конца сборки.

На верхней грани необходимо найти самый большой прямоугольник и поставить его на угол. При этом могут быть два варианта:

Ребро должно перейти вниз и вправо. Сделать это можно с помощью такой комбинации:

• Верхняя часть – за часовой стрелкой;
• правая грань – за часовой стрелкой;
• верх – против часовой стрелки;
• правая часть – против часовой стрелки;
• верх – против часовой стрелки;
• передняя часть – против часовой стрелки;
• верх – за часовой стрелкой;
• передняя часть – за часовой стрелкой.

Во втором случае кубик с нужной деталью возьмите центром к себе. Ребро должно перейти вниз и влево таким способом:

• Верх – против часовой стрелки;
• левая грань – против часовой стрелки;
• верх – за часовой стрелкой;
• левая часть – за часовой стрелкой;
• верх – за часовой стрелкой;
• передняя часть – за часовой стрелкой;
• верх – против часовой стрелки;
• передняя грань – против часовой стрелки.

На уроках математики в школе

Решение магических квадратов на уроках математики и внеклассных занятиях вызывает интерес, способствует развитию мышления. Дети учатся планировать и контролировать свою работу. В клетки магических квадратов можно записывать не только числа, но и выражения. Все зависит от изучаемой темы. Задания с магическими квадратами часто дают как дополнительные или олимпиадные уже в начальной школе.

Один из способов решения магического квадрата

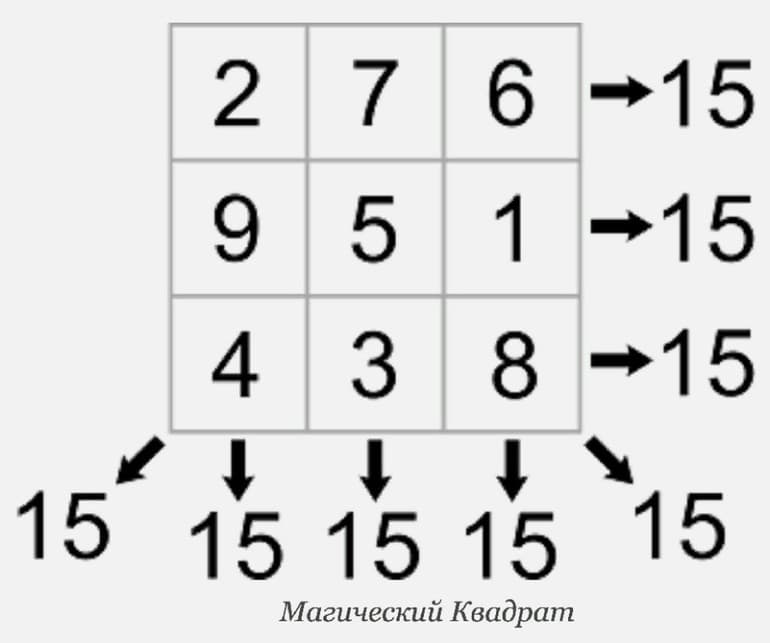
Нетрудно решить магический квадрат третьего порядка (у которого по три столбца и строки). Можно воспользоваться тем фактом, что число (выражение), стоящее на пересечении его диагоналей, всегда равно ⅓ волшебной суммы. Отсюда следует алгоритм построения:

1. Вписываем  в первую строку или столбец 3 любых числа.

1. Вычисляем магическую сумму (0 + 2 + 4 = 6).
2. Ищем ее третью часть (6/3 = 2).
3. Полученное число записываем на пересечении диагоналей.

1. Подбираем остальные числа и заполняем ими пустые клеточки квадрата.

Как изготовить игру

Итак, понадобится картон и цветная бумага. В идеале каждый квадратик должен быть своего цвета, поэтому и оттенков у цветной бумаги должно быть столько, сколько квадратиков вы планируете сделать. У Никитиных в книге 24 квадрата, но можно сделать и 20, и 30, и вообще любое количество, на которое хватит вашей фантазии при разметке деталей.

У нас было три комплекта по 36 квадратов.

Почему три? Все очень просто. В эту игру интересно играть на скорость — устроить соревнование, кто быстрее соберет заданное количество квадратиков. А соревнование подразумевает как минимум двоих, а лучше больше, участников.

Берем картон и аккуратно нарезаем его на квадраты. Сторона квадрата у Никитиных была задана и равнялась 8 см. Почему? Не знаю. У нас было три комплекта разных размеров — 5 см, 8 см и 10 см. Для малышей удобнее, конечно, более крупные детали, а для детей постарше — разницы нет.

На картонные квадраты наклеиваем цветную бумагу и сушим под прессом. Кстати, если у вас качественный картон, его можно просто покрасить!

На неокрашенную сторону наносим разметку, затем аккуратно разрезаем квадраты. Тут нельзя торопиться. Разрезав квадратик на детали, каждую из них нужно обязательно пронумеровать. Например, квадратик номер 7 состоит из 3 деталей. Их нужно так и подписать 7-1, 7-2, 7-3. Это поможет быстро найти нужные детали в общей куче.

Желательно заранее склеить или купить конвертики, по числу ваших квадратов. И каждый разрезанный квадрат поместить в свой конверт. Конверт тоже пронумеровать.

Варианты для разметки квадратов можно посмотреть здесь:

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: : 2 = (6 х 37): 2 = 222:2.

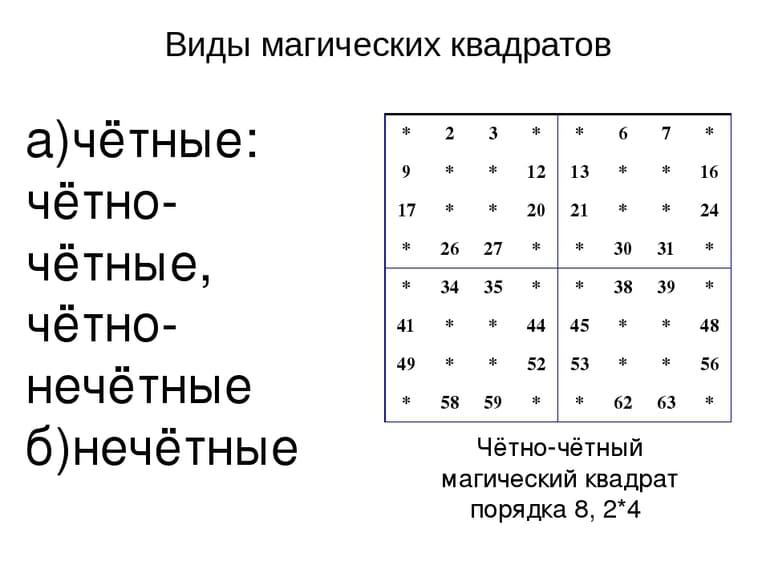
Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.
Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.

Алгоритм действий:

Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.
Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.
Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.
В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.
Таким же способом строят промежуточный квадрат А3.
Эти 3 промежуточных фигуры формируют выделенную область А.
Далее переходят в квадрант D и формируют обособленную область D.

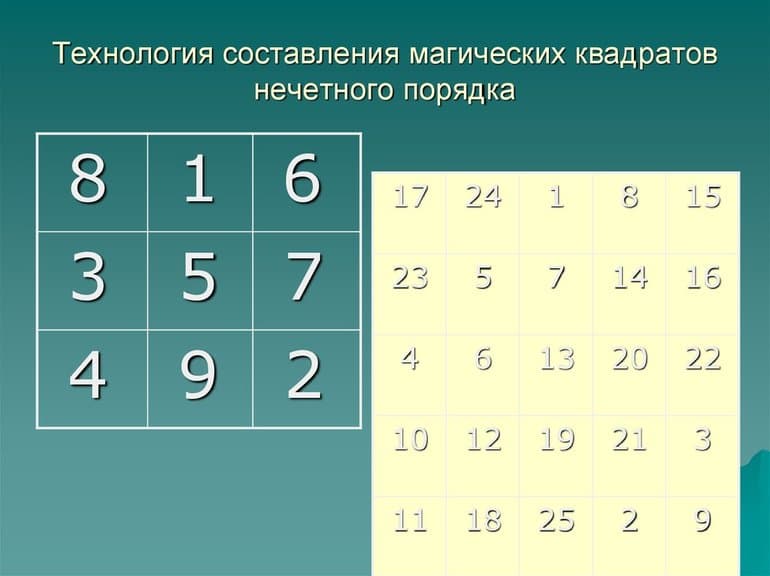
Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

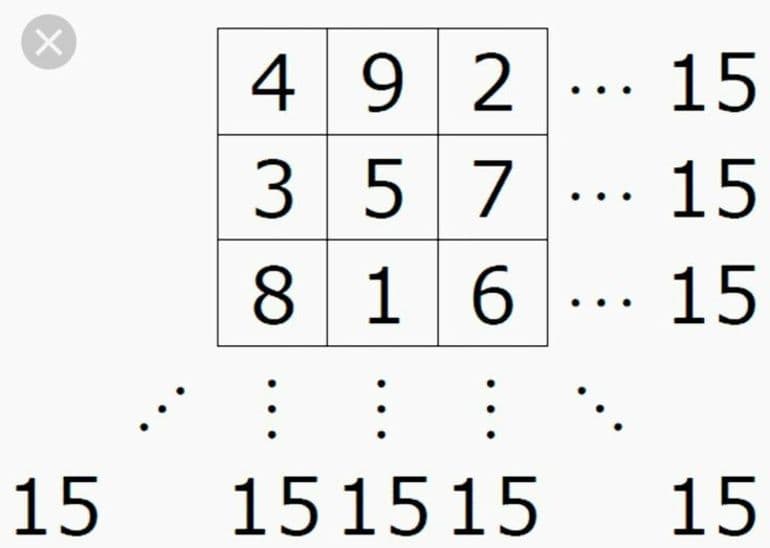
Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.
Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.
В средней клетке верхней строки вписывается 1.
Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.
По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.
Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.
Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.
Поскольку место цифры 7 уже занято, она вписывается ниже 6.
Восьмёрка занимает место в левом нижнем углу.
Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

https://youtube.com/watch?v=5W0aUXUzA14

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Общие сведения

В первую очередь следует сказать, что изготавливать головоломки из дерева своими руками не менее увлекательно, чем разгадывать. Причем в их изготовлении нет ничего сложного, поэтому справиться с этой задачей может каждый.

Единственное, для этого понадобится простой набор инструментов, который имеется у каждого домашнего мастера:

• Лобзик (желательно электролобзик);
• Стамески;
• Электродрель;
• Напильники и надфили;
• Наждачная бумага.

Что касается материалов, то чаще всего требуются:

• Небольшие досочки;
• Бруски;
• Листы фанеры;
• Лак по дереву.

Даже если под рукой этих материалов не оказалось, их можно приобрести в строительном магазине. Цена на них обычно невысокая.

Крест ОСС

Как играть в «Сложи квадрат»

В этой игре нет четких правил и требований.

Для самых маленьких можно придумать сказку-историю. Например, про строительство дороги из квадратов. Первый квадратик вынимаем из конверта. Он целый! Укладываем в начало дороги. Достаем второй.

-Ой, кто-то испортил наш квадратик. как бы нам его починить?

Для начала предлагаем ребенку детали, повернутые окрашенной стороной вверх, чтобы ему было легче ориентироваться. Затем, когда ребенок поймет, что надо из деталей сложить  квадратик, можно разрешить ему самому доставать детали из конверта.

Если ребенок уже различает цвета, можно смешать детали нескольких квадратов вместе, тем самым значительно усложнив задачу. Ведь в начале нужно выбрать все детали одного цвета!

Дети постарше с удовольствием устраивают соревнования на скорость.

Кстати, некоторые квадраты  не так-то просто будет сложить и вам, не смотря на то, что вы сами их изготовили!

Интересной и полезной игры ВАМ!