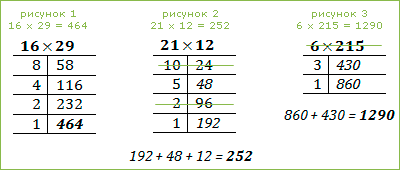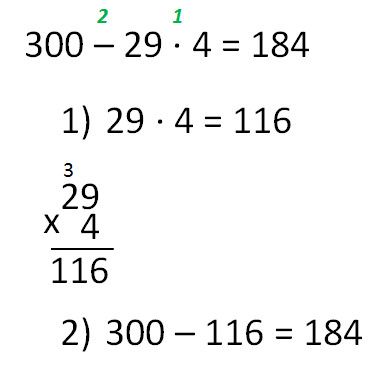Умножение на 11
Содержание:
- Таблица умножения на 11
- Ввод команд в наш онлайн-калькулятор с клавиатуры ПК
- Улучшаем навыки счета с помощью IQКлуб
- Умножение столбиком. Примеры умножения в столбик, нахождения решения онлайн.
- Таблица умножения до 20 и до 100
- Как быстро умножать двузначные числа в уме?
- Обратите внимание!
- Калькулятор умножение в столбик онлайн
- Как научить детей таблице умножения один раз и на всю жизнь
Таблица умножения на 11
| Множители | Произведение (Результат) |
|---|---|
| 11 * 1 = | 11 |
| 11 * 2 = | 22 |
| 11 * 3 = | 33 |
| 11 * 4 = | 44 |
| 11 * 5 = | 55 |
| 11 * 6 = | 66 |
| 11 * 7 = | 77 |
| 11 * 8 = | 88 |
| 11 * 9 = | 99 |
| 11 * 10 = | 110 |
| 11 * 11 = | 121 |
| 11 * 12 = | 132 |
| 11 * 13 = | 143 |
| 11 * 14 = | 154 |
| 11 * 15 = | 165 |
| 11 * 16 = | 176 |
| 11 * 17 = | 187 |
| 11 * 18 = | 198 |
| 11 * 19 = | 209 |
| 11 * 20 = | 220 |
| 11 * 21 = | 231 |
| 11 * 22 = | 242 |
| 11 * 23 = | 253 |
| 11 * 24 = | 264 |
| 11 * 25 = | 275 |
| 11 * 26 = | 286 |
| 11 * 27 = | 297 |
| 11 * 28 = | 308 |
| 11 * 29 = | 319 |
| 11 * 30 = | 330 |
| 11 * 31 = | 341 |
| 11 * 32 = | 352 |
| 11 * 33 = | 363 |
| 11 * 34 = | 374 |
| 11 * 35 = | 385 |
| 11 * 36 = | 396 |
| 11 * 37 = | 407 |
| 11 * 38 = | 418 |
| 11 * 39 = | 429 |
| 11 * 40 = | 440 |
| 11 * 41 = | 451 |
| 11 * 42 = | 462 |
| 11 * 43 = | 473 |
| 11 * 44 = | 484 |
| 11 * 45 = | 495 |
| 11 * 46 = | 506 |
| 11 * 47 = | 517 |
| 11 * 48 = | 528 |
| 11 * 49 = | 539 |
| 11 * 50 = | 550 |
| 11 * 51 = | 561 |
| 11 * 52 = | 572 |
| 11 * 53 = | 583 |
| 11 * 54 = | 594 |
| 11 * 55 = | 605 |
| 11 * 56 = | 616 |
| 11 * 57 = | 627 |
| 11 * 58 = | 638 |
| 11 * 59 = | 649 |
| 11 * 60 = | 660 |
| 11 * 61 = | 671 |
| 11 * 62 = | 682 |
| 11 * 63 = | 693 |
| 11 * 64 = | 704 |
| 11 * 65 = | 715 |
| 11 * 66 = | 726 |
| 11 * 67 = | 737 |
| 11 * 68 = | 748 |
| 11 * 69 = | 759 |
| 11 * 70 = | 770 |
| 11 * 71 = | 781 |
| 11 * 72 = | 792 |
| 11 * 73 = | 803 |
| 11 * 74 = | 814 |
| 11 * 75 = | 825 |
| 11 * 76 = | 836 |
| 11 * 77 = | 847 |
| 11 * 78 = | 858 |
| 11 * 79 = | 869 |
| 11 * 80 = | 880 |
| 11 * 81 = | 891 |
| 11 * 82 = | 902 |
| 11 * 83 = | 913 |
| 11 * 84 = | 924 |
| 11 * 85 = | 935 |
| 11 * 86 = | 946 |
| 11 * 87 = | 957 |
| 11 * 88 = | 968 |
| 11 * 89 = | 979 |
| 11 * 90 = | 990 |
| 11 * 91 = | 1001 |
| 11 * 92 = | 1012 |
| 11 * 93 = | 1023 |
| 11 * 94 = | 1034 |
| 11 * 95 = | 1045 |
| 11 * 96 = | 1056 |
| 11 * 97 = | 1067 |
| 11 * 98 = | 1078 |
| 11 * 99 = | 1089 |
| 11 * 100 = | 1100 |
| … * 101 = | … |
Ввод команд в наш онлайн-калькулятор с клавиатуры ПК
Работа с калькулятором довольно проста и не вызовет сложностей ни у кого. Для ввода цифр используются клавиши компьютерной клавиатуры с цифрами или цифровые клавиши справа на дополнительной панели.
Чтобы стереть неправильно введенный символ используйте клавишу .
Чтобы получить результат сложения или вычитания, жмите клавишу равно – используйте для этого .
Чтобы использовать знак «плюс», жмите на клавиатуре клавишу . Она расположена на дополнительной клавиатуре справа вверху.
Чтобы использовать знак «минус», жмите на клавиатуре клавишу . Она расположена сверху или на дополнительной клавиатуре.
Для умножения или деления используйте знаки и [ / ] соответственно, которые расположены на боковой клавиатуре.
Чтобы обнулить все расчеты или начать подсчет сначала, нажмите , на верхней клавиатуре или же используйте кнопку на боковой клавиатуре.
Простые примеры вычислений, используя калькулятор онлайн с корнями
Возвести число 2 в степень 3: 23. Результат — 8.
Вычисление квадратного корня числа 625: 625 . Результат — 25.
Вычисление процента от числа: 1000 20 . Результат — 200.
Прибавление процента к числу: 800 25 . Результат — 1000.
Вычитание процента из числа: 800 25 . Результат — 600.
Часто задаваемые вопросы
У пользователей достаточно часто возникает вопрос: почему если на калькуляторе посчитать 3+3х3=18, то калькулятор, вероятно, считает неверно? Нет, калькулятор считает абсолютно правильно. При вводе очередного математического действия онлайн калькулятор делает подитог
Рекомендуем при проведении подсчетов обращать внимание на дисплей текущих действий. Он расположен справа под основным дисплеем
А теперь попробуем посчитать:
3+3=6, подитог 6. Далее: 6х3=18. Правильный ответ – 18. Ошибок в данном случае нет.
Из истории возникновения калькуляторов
Основным прародителем современного калькулятора считается абак – доска со специальными углублениями, по которым перемещали счетные метки (в большинстве случаев это были косточки или камни). Впервые абак был замечен в Древнем Вавилоне около 3000 лет до н.э. В Древней Греции такой вычислительный прибор появился только в V веке до н.э.
В России абак появился только в 16 веке. Первые русские счеты были выполнены из натуральной древесины. Счетными метками были вишнёвые косточки.
Если вам понравились наши сервисы, поделитесь ими с друзьями! Нет ничего проще, когда за вас делает расчет онлайн калькулятор!
Помимо обычного калькулятора у нас на сайте вы можете встретить: калькулятор корней (в том числе вы можете выполнить умножение корней, деление, сложение и вычитание квадратных корней), калькулятор онлайн с корнями и дробями (математический) и прочие!
Улучшаем навыки счета с помощью IQКлуб
Если вашему ребенку от 3 до 14 лет, развить его интеллект, навыки счета, чтения, улучшить память и внимание помогут развивающие игры на сайте IQКлуб. К разработке игр со всей серьезностью подошли настоящие профессионалы: лучшие педагоги, психологи, ученые и дизайнеры
Они позаботились о том, чтобы игры не содержали рекламы и платного контента. Созданные программы учитывают возраст детей. Более того, для каждого маленького пользователя формируется индивидуальный план обучения. А родители в режиме онлайн могут наблюдать за ходом развития своего чада. Воспользовавшись сервисом IQКлуб, современные дети, без сомнения, останутся довольными, так как в их распоряжении будет интереснейший и познавательный игровой мир.
Умножение столбиком. Примеры умножения в столбик, нахождения решения онлайн.
Калькулятор
умножение чисел столбиком
Рассчитать
Очистить
|
\begin{align} |
Введите числа и калькулятор умножит числа столбиком и отобразит подробное решение.
Умножение в столбик
введение
Нахождение произведения чисел
Метод умножения столбиком, позволяет упростить умножения чисел.
Умножение столбиком предполагает последовательное умножения первого числа,
на все цифры второго числа последующего сложения полученных произведений с учетом отступа,
зависящего от положения цифры второго числа.
Рассмотрим как нужно умножать столбиком на примере нахождения произведения двух чисел
625 × 25.
-
1 Запишем числа одно под другим и проведем
черту . -
2 Число 25, состоит из
2 цифр, 2 и 5, будем умножать первое
число 625, на цифры второго числа в обратном порядке.
Начнем вычисление с нахождения произведения 625 × 5,
запишем результат ниже черты, начинаем запись с правой стороны, получим: . -
3 Теперь умножаем 625 на
2, и запишем результат на следующей строке, сместив запись на одну
клетку левее,
предыдущего произведения, получим .При большем количестве цифр во втором числе, мы получим что наши произведения
выстраиваются справа в виде «лесенки». -
4 В результате умножения получаем
2 произведения, 3125 и 1250,
будем последовательно справа на лево складывать их цифры между собой, в том порядке как
они идут, и записывать результат их сложения ниже. Если сумма цифр при сложение превысит
9, то делим сумму на 10,
остаток от деления записываем под текущими цифрами, а целую часть от деления перенесем
влево.В результате получаем .
Таблица умножения до 20 и до 100
Умножение до 100 в виде таблицы равенств из-за ее громоздкости, как правило, не представляют. Пользуются фрагментами большой квадратной таблицы с соответствующими значениями. Принцип поиска по этим таблицам точно такой же: число в ячейке на пересечении столбца и строки с нужными множителями — есть искомое значение. При необходимости из этих фрагментов составляется одна большая таблица умножения до 100. Приведем пример. Необходимо умножить 95 на 87. Видим, что оба этих значения есть в последней таблице. Находим в столбце число 95, в строке число 87. Смотрим, что на пересечении их находится значение 8265. Таким образом, 95х87= 8265. Подобные таблицы оказываются под рукой нечасто, поэтому для таких вычислений на практике люди чаще пользуются калькуляторами. Тем более, калькуляторы сейчас есть в каждом смартфоне. Кроме того существуют специальные способы счета, которые позволяют в том числе и выполнять умножение двузначных чисел, например ментальная арифметика и счет с помощью пальцев. О них мы напишем в специальном разделе. Тем не менее таблицы с уже посчитанными значениями приведены ниже для ознакомления. Также при желании их можно скачать и распечатать, для этого нужно использовать ссылку или же нажать правую кнопку мышки над картинкой и выбрать вариант «сохранить картинку как».





Как быстро умножать двузначные числа в уме?
Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.
Выбираем традиционные методы
Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.
Умножение с помощью разложения чисел
Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки. Четыре полученных числа суммируются
Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме
Например, для умножения 38 на 57 необходимо:
- разложить число на (30+8)*(50+7);
- 30*50 = 1500 – запомнить результат;
- 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
- (1500 + 610) + 8*7 = 2110 + 56 = 2166
Умножение в столбик в уме
Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:
- 47*1 = 47 – запомнить;
- 47*8 = 376 – запоминаем;
- 376*10 + 47 = 3807.
Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.
Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.
Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.
Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143
Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308
Главное — тренироваться непрерывно!
Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.
- Каждое число необходимо представить как разницу 100 и еще одного числа:(100 — 13)*(100 — 9)Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.87 – 9 = 7891 – 13 = 78
- Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
- В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.
https://youtube.com/watch?v=LHnFXJnLdKE
Поделиться статьей с друзьями!
Обратите внимание!
Правило про умножение на 11, которое мы выучили выше, «работает», если сумма первой и последней цифр – не больше 9. Если это число больше – нужно учесть важный нюанс.
Например, умножаем 67 на 11.
6_7
- Складываем 6 + 7 = 13.
- Из числа 13 единицу прибавляем к шестерке, а тройку вписываем посередине.
- Ответ: 737.
Не верите? Проверьте на калькуляторе.
В принципе, метод умножения любого числа на 11 состоит в том, что суммируются соседние числа.
Например, умножим число 32617 на 11:
- 3______7
- 3(3+2)(2+6)(6+1)(1+7)7
- Ответ: 358787
Если сумма в скобках больше 9, применяем тот же метод, что и с двухзначными числами.
Как видим, хоть ответ получился и «внушительным», получили мы его довольно просто.
Если придется умножать большие числа на 11, советуем:
- Легче считать, если цифры можно визуально зафиксировать.
- Обязательно проверяйте ответ, чтобы ничего не перепутать и не сбиться.
Вы спросите, а зачем вообще нужна такая «тренировка»? Отвечаем:
Во-первых, это интересно и познавательно. Кстати, и школьнику, и родителям.
Во-вторых, ваш ребенок может оказаться в ситуации (например, на олимпиаде), где не разрешат пользоваться калькулятором. А ваш ученик к этому уже готов.
В-третьих, умея решать такие занимательные примеры, ваш ребенок сможет и сам полюбить математику, и приобщить к ней своих друзей.
Калькулятор умножение в столбик онлайн
Не секрет, что знакомство с математикой начинается с важнейшей науки о числах — арифметики. Как утверждал великий ученый М. В. Ломоносов, с арифметикой мы входим «во врата учености», именно с нее начинается нелегкий, но заманчивый путь познания мира. Эта наука изучает числа и действия над ними. Одним из таких действий над цифрами является умножение столбиком. Без ясного понимания последовательности действий при совершении умножения двух чисел в математике нельзя двигаться дальше. Следует знать, что числа, которые умножаются, называются множителями, а полученный результат — произведением. В числах имеются разряды, самый маленький — единицы, затем десятки, после них сотни и т. д. Если вы умножаете в столбик, расположите оба множителя друг над другом, чтобы совпадали разряды чисел. Большее число расположите в верхней строке, меньшее — в нижней. Если оба множителя или один из них имеют на концах нули, то числа располагают так, чтобы цифры наименьшего разряда (кроме 0) находились в одном столбике. Нули в поле поэтапных операций не заносятся, они переносятся под черту в конечный результат. Это делается потому, что при умножении любого числа на 0, все равно получается 0. Слева от множителей ставим «х». Умножение в столбик — поразрядное умножение. Это значит, что каждый разряд 1-го множителя, начиная с последней цифры, умножается на последнюю цифру 2-го множителя. Следующей строкой будет результат умножения верхнего числа (1-го множителя) на следующую цифру нижнего числа (2-го множителя). Следует помнить, что полученный после умножения на вторую цифру результат, следует размещать под второй цифрой полученного результата от первого умножения. Поэтапные произведения (разрядные) складываются по разрядам, результат заносится под черту, начиная с самой правой стороны. Слева от полученных произведений, которые складываются, ставим «+».
Как научить детей таблице умножения один раз и на всю жизнь

Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,что открываете эту
красоту. Спасибо за вдохновение и мурашки.Присоединяйтесь к нам в
и
Таблица умножения — базовое понятие в математике, с которым мы знакомимся еще в начальной школе и которое потом используем всю жизнь вне зависимости от профессии. Вот только дети не спешат заучивать бесконечные столбики наизусть, особенно если задание пришлось на каникулы.
AdMe.ru даст советы, как легко выучить таблицу вместе с детьми и сделать этот процесс увлекательным.
Таблица Пифагора
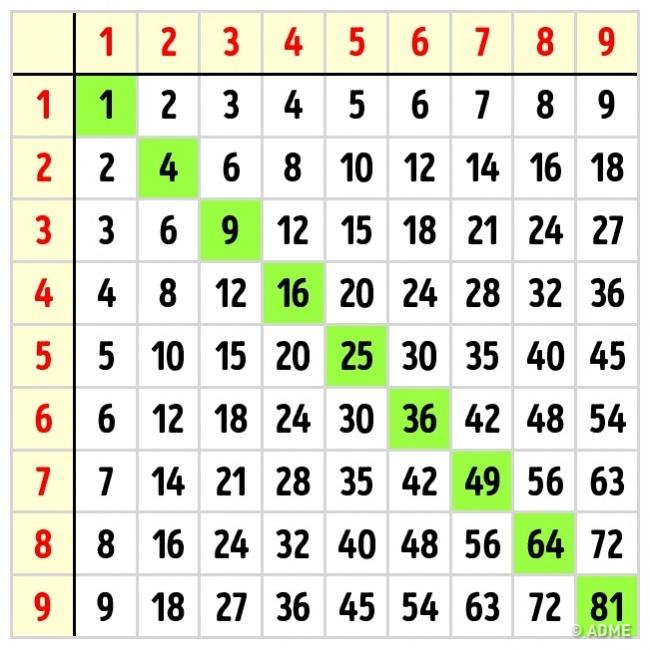
Несмотря на то что задача — выучить, то есть заучить, таблицу наизусть, прежде всего важно понять суть самого действия. Для этого можно заменить умножение сложением: одинаковые числа складываются столько раз, на сколько мы умножаем
Например, 6×8 — это сложить 8 раз по 6.
Выделяем цветом одинаковые значения
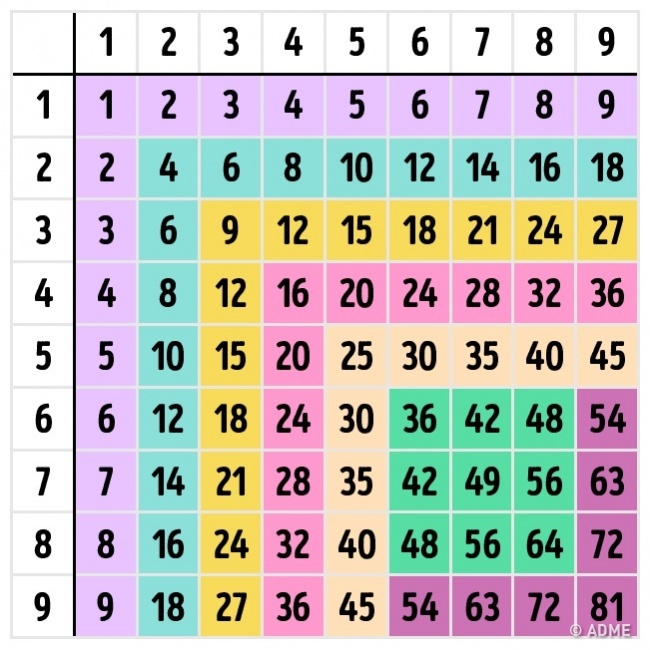
Отличным помощником для изучения умножения станет таблица Пифагора, которая также демонстрирует некоторые закономерности. Например то, что от перемены мест множителей произведение не меняется: 4×6 = 6×4. Отметьте такие «зеркальные» ответы определенным цветом — это поможет запомнить и не запутаться при повторении.
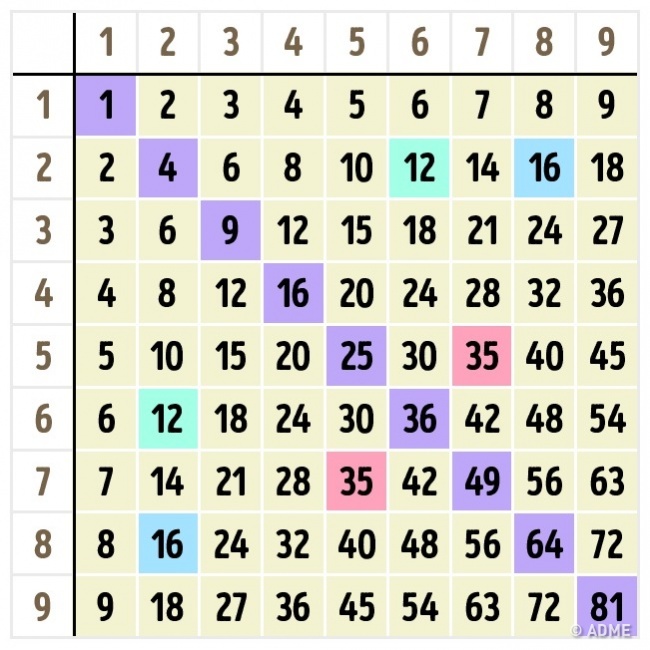
Начинать изучение таблицы Пифагора лучше с самых простых и понятных частей: умножения на 1, 2, 5 и 10. При умножении на единицу число остается неизменным, а умножение на 2 дает нам удвоенное значение. Все ответы умножения на 5 оканчиваются либо на 0, либо на 5. А вот умножив на 10, в ответе мы получим двузначное число из цифры, которую умножали, и нуля.
Таблица для закрепления результата
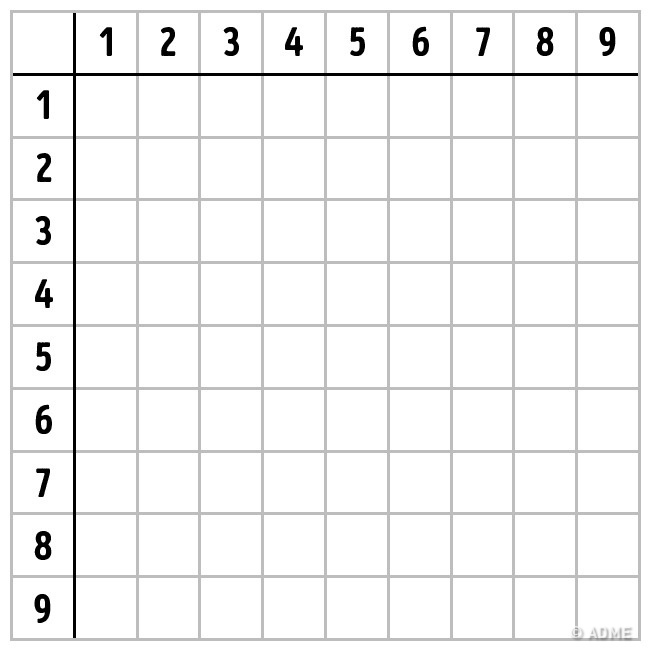
Для закрепления результатов нарисуйте с ребенком пустую таблицу Пифагора и предложите ему заполнить клеточки правильными ответами. Для этого вам понадобится всего лишь листок бумаги, карандаш и линейка. Нужно нарисовать квадрат и поделить его на 10 частей по вертикали и горизонтали. А затем заполнить верхнюю строч