Закон больших чисел

Доказательство слабого закона

Рассмотрим бесконечную последовательность X1,X2,…{\displaystyle X_{1},X_{2},…} независимых и одинаково распределенных случайных величин с конечным математическим ожиданием E(X1)=E(X2)=…=μ<∞{\displaystyle E(X_{1})=E(X_{2})=…=\mu <\infty }, нас интересует сходимость по вероятности

X¯n=1n(X1+⋯+Xn).{\displaystyle {\overline {X}}_{n}={\tfrac {1}{n}}(X_{1}+\cdots +X_{n}).}

Теорема: X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }

Предположение о конечной дисперсии D(X1)=D(X2)=…=σ2<∞{\displaystyle D(X_{1})=D(X_{2})=…=\sigma ^{2}<\infty } не является обязательным. Большая или бесконечная дисперсия замедляет сходимость, но ЗБЧ выполняется в любом случае.

Это доказательство использует предположение о конечной дисперсии D⁡(Xi)=σ2{\displaystyle \operatorname {D} (X_{i})=\sigma ^{2}} (для всех i{\displaystyle i}). Независимость случайных величин не предполагает корреляции между ними, мы имеем

D⁡(X¯n)=D⁡(1n(X1+⋯+Xn))=1n2D⁡(X1+⋯+Xn)=nσ2n2=σ2n.{\displaystyle \operatorname {D} ({\overline {X}}_{n})=\operatorname {D} ({\tfrac {1}{n}}(X_{1}+\cdots +X_{n}))={\frac {1}{n^{2}}}\operatorname {D} (X_{1}+\cdots +X_{n})={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}.}

Математическое ожидание последовательности μ{\displaystyle \mu } представляет собой среднее значение выборочного среднего:

E(X¯n)=μ.{\displaystyle E({\overline {X}}_{n})=\mu .}

Используя неравенство Чебышева для X¯n{\displaystyle {\overline {X}}_{n}}, получаем

P⁡(|X¯n−μ|≥ε)≤σ2nε2.{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geq \varepsilon )\leq {\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.}

Это неравенство используем для получения следующего:

P⁡(|X¯n−μ|<ε)=1−P⁡(|X¯n−μ|≥ε)≥1−σ2nε2,{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|<\varepsilon )=1-\operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geq \varepsilon )\geq 1-{\frac {\sigma ^{2}}{n\varepsilon ^{2}}},}

при n→∞{\displaystyle n\rightarrow \infty }, выражение стремится к 1{\displaystyle {\mathit {1}}},

теперь по определению сходимости по вероятности мы получим:

X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }.

Доказательство с использованием сходимости характеристических функций

По теореме Тейлора для комплексных функций, характеристическая функция любой случайной величины X{\displaystyle X} с конечным средним μ{\displaystyle \mu } может быть записана как

φX(t)=1+itμ+o(t),t→{\displaystyle \varphi _{X}(t)=1+it\mu +o(t),\quad t\rightarrow 0.}

Все X1,X2,…{\displaystyle X_{1},X_{2},…} имеют одну и ту же характеристическую функцию, обозначим её как φX{\displaystyle \varphi _{X}}.

Среди основных свойств характеристических функций выделим два свойства

φ1nX(t)=φX(tn){\displaystyle \varphi _{{\frac {1}{n}}X}(t)=\varphi _{X}({\tfrac {t}{n}})} и φX+Y(t)=φX(t)φY(t){\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)}, X{\displaystyle X} и Y{\displaystyle Y}независимы

Эти правила могут быть использованы для вычисления характеристической функции X¯n{\displaystyle {\overline {X}}_{n}} в терминах φX{\displaystyle \varphi _{X}}

φX¯n(t)=φX(tn)n=1+iμtn+o(tn)n→eitμ,{\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left^{n}=\left^{n}\,\rightarrow \,e^{it\mu },} при n→∞.{\displaystyle n\rightarrow \infty .}

Предел eitμ{\displaystyle e^{it\mu }}является характеристической функцией непрерывной случайной величины μ{\displaystyle \mu } и, следовательно, по теореме непрерывности Леви, X¯n{\displaystyle {\overline {X}}_{n}}сходится по распределению к μ{\displaystyle \mu }:

X¯n→Dμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {D}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Поскольку μ{\displaystyle \mu }- константа, то отсюда следует, что сходимость по распределению к μ{\displaystyle \mu } и сходимость по вероятности к μ{\displaystyle \mu } эквивалентны. Поэтому,

X¯n→Pμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {P}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Это показывает, что среднее значение выборки по вероятности сходится к производной характеристической функции в начале координат, если она существует.

Объяснение для того, кто всё же не понял

Бросая монету в игре «орёл или решка» вы вправе ожидать равного числа выпадений любой стороны монеты. Если вдруг монета пять раз подряд выпала «решкой» — о чём это говорит? Или если одна команда обыгрывает равную ей по силе уже пять сезонов подряд – что в этом результате?

Ровным счётом ничего. У монеты нет памяти, которая подсказала бы ей, что решка была в последнее время в фаворе. А состав любой команды за несколько лет может обновиться более чем наполовину. Перед каждым событием вероятность того или иного исхода никак не зависит от предыдущего. Естественно, с точки зрения математики. Вероятность – хорошо видимая на небе звезда, по ней можно ориентироваться в сумрачном мире беттинга, но расстояние до неё слишком велико, чтобы дотянуться или рассмотреть поближе.

Это важно повторить. События в своей последовательности никак не влияют друг на друга, но если их становится много, противоположные исходы стараются разойтись равными группами по разным сторонам

Притом, если у монеты есть два абсолютно равных между собой исхода, то для статистики встречи равных команд перекос всё же имеется, пусть и незначительный. Да и не стоит забывать про возможность ничьи.

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Высшая математика мини-справочник для ВУЗов

Закон больших чисел — ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Закон больших чисел — это совокупность предложений, в которых утверждается, что с вероятностью сколь угодно близкой к единице отклонение средней арифметической достаточно большого числа случайных величин от постоянной величины, равной средней арифметической их математических ожиданий, не превзойдет заданного сколь угодно малого числа ε > 0.

Неравенство Маркова. Если случайная величина X не принимает отрицательных значений и δ — произвольная положительная величина, то вероятность того, что значения случайной величины X не превзойдут величины δ, не превысит 1 – a/δ, где а есть математическое ожидание X

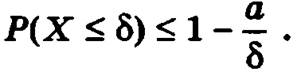
Неравенство Чебышева. Вероятность того, что отклонение случайной величины от ее математического ожидания превзойдет по модулю положительное число 5, не больше дроби, числитель которой есть дисперсия случайной величины, а знаменатель — квадрат δ:

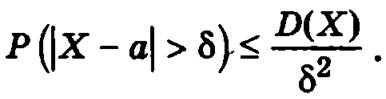
Теорема Чебышева. Если дисперсия попарно независимых случайных величин не превосходит заданного положительного числа С, то вероятность того, что абсолютное отклонение средней арифметической таких величин от средней арифметической их математических ожиданий меньше некоторого числа е, с возрастанием количества случайных величин становится сколь угодно близкой к единице

где X1, Х2, …, Xn — случайные величины, a1, a2, …, an — их математические ожидания, ε > 0, δ > 0.

Следствие из теоремы Чебышева. Если независимые случайные величины имеют одинаковые равные а математические ожидания, дисперсии их ограничены одной и той же постоянной С, а их число достаточно велико, то, как бы ни было мало данное число ε > 0, вероятность того, что отклонение средней арифметической этих случайных величин от а не превысит по абсолютной величине ε, сколь угодно близка к единице

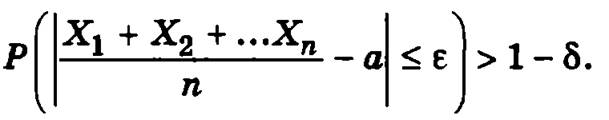
Теорема Пуассона. Если вероятность рi наступления события А в i-м испытании (i = 1, 2, …, n) не меняется, когда становится известным исход предыдущих испытаний, а число испытанийn достаточно велико, то вероятность того, что относительная частота события А будет сколь угодно мало отличаться от средней арифметической вероятностей pi, сколь угодно мала.

Теорема Бернулли. Если вероятность p наступления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что относительная частота события А будет сколь угодно мало отличаться от его вероятности, сколь угодно близка к единице.

Теорема Ляпунова. Если имеется п независимых случайных величин X1, Х2, …, Хn с математическими ожиданиями a1, а2, …, аn и с дисперсиями D(X1), D(X2), …, D(Xn), причем отклонения всех случайных величин от их математических ожиданий не превышают по абсолютной величине одного и того же числа ε > 0:

|Xi – ai| ≤ ε,

а все дисперсии ограничены одним и тем же числом С:

D(Хi) ≤ С,

то при достаточно большом п сумма случайных величин X1, Х2, …, Хn будет подчинена закону распределения, как угодно близкому к закону нормального распределения.

Предыдущая

Следующая

Алгебраическая теория чисел

Основная статья: Алгебраическая теория чисел

В алгебраической теории чисел понятие целого числа расширяется, в качестве алгебраических чисел рассматривают корни многочленов с рациональными коэффициентами. Была разработана общая теория алгебраических и трансцендентных чисел. При этом аналогом целых чисел выступают целые алгебраические числа, то есть корни унитарных многочленов с целыми коэффициентами. В отличие от целых чисел, в кольце целых алгебраических чисел не обязательно выполняется свойство факториальности, то есть единственности разложения на простые множители.

Теория алгебраических чисел обязана своим появлением изучению диофантовых уравнений, и в том числе попыткам доказать теорему Ферма. Куммеру принадлежит равенство

xn=zn−yn=∏i=1n(z−aiy),{\displaystyle x^{n}=z^{n}-y^{n}=\prod _{i=1}^{n}(z-a_{i}y),}

где ai{\displaystyle a_{i}} — корни степени n{\displaystyle n} из единицы.
Таким образом Куммер определил новые целые числа вида z+aiy{\displaystyle z+a_{i}y}. Позднее Лиувилль показал, что если алгебраическое число является корнем уравнения степени n{\displaystyle n}, то к нему нельзя подойти ближе чем на Q−n{\displaystyle Q^{-n}}, приближаясь дробями вида PQ{\displaystyle P/Q}, где P{\displaystyle P} и Q{\displaystyle Q} — целые взаимно простые числа.

После определения алгебраических и трансцендентных чисел в алгебраической теории чисел выделилось направление, которое занимается доказательством трансцендентности конкретных чисел, и направление, которое занимается алгебраическими числами и изучает степень их приближения рациональными и алгебраическими.

Алгебраическая теория чисел включает в себя такие разделы, как теорию дивизоров, теорию Галуа, теорию полей классов, дзета- и L-функции Дирихле, когомологии групп и многое другое.[источник не указан 1556 дней]

Одним из основных приёмов является вложение поля алгебраических чисел в своё пополнение по какой-то из метрик — архимедовой (например, в поле вещественных или комплексных чисел) или неархимедовой (например, в поле p-адических чисел).

Геометрия чисел.

В общих чертах можно сказать, что геометрия чисел включает в себя все приложения геометрических понятий и методов к теоретико-числовым проблемам. Отдельные соображения такого рода появились в 19 в. в работах Гаусса, П.Дирихле, Ш.Эрмита и Г.Минковского, в которых для решения некоторых неравенств или систем неравенств в целых числах использовались их геометрические интерпретации. Минковский (1864–1909) систематизировал и унифицировал все, сделанное в этой области до него, и нашел новые важные приложения, особенно в теории линейных и квадратичных форм. Он рассматривал n неизвестных как координаты в n-мерном пространстве. Множество точек с целыми координатами получило название решетки. Все точки с координатами, удовлетворяющими требуемым неравенствам, Минковский интерпретировал как внутренность некоторого «тела», и задача состояла в том, чтобы определить, содержит ли данное тело какие-либо точки решетки. Фундаментальная теорема Минковского утверждает, что если тело выпукло и симметрично относительно начала координат, то оно содержит хотя бы одну точку решетки, отличную от начала координат, при условии, что n-мерный объем тела (при n = 2 это площадь) больше, чем 2n.

Многие вопросы естественно приводят к теории выпуклых тел, и именно эта теория была развита Минковским наиболее полно. Затем на долгое время опять наступил застой, но с 1940, в основном благодаря работам английских математиков, наметился прогресс в развитии теории невыпуклых тел.

Варианты

Доказательство слабого закона

Рассмотрим бесконечную последовательность X1,X2,…{\displaystyle X_{1},X_{2},…} независимых и одинаково распределенных случайных величин с конечным математическим ожиданием E(X1)=E(X2)=…=μ<∞{\displaystyle \mathbb {E} (X_{1})=\mathbb {E} (X_{2})=\ldots =\mu <\infty }, нас интересует сходимость по вероятности

X¯n=1n(X1+⋯+Xn).{\displaystyle {\overline {X}}_{n}={\tfrac {1}{n}}(X_{1}+\cdots +X_{n}).}

Теорема: X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }

Предположение о конечной дисперсии D(X1)=D(X2)=…=σ2<∞{\displaystyle D(X_{1})=D(X_{2})=\ldots =\sigma ^{2}<\infty } не является обязательным. Большая или бесконечная дисперсия замедляет сходимость, но ЗБЧ выполняется в любом случае.

Это доказательство использует предположение о конечной дисперсии D⁡(Xi)=σ2{\displaystyle \operatorname {D} (X_{i})=\sigma ^{2}} (для всех i{\displaystyle i}). Независимость случайных величин не предполагает корреляции между ними, мы имеем

D⁡(X¯n)=D⁡(1n(X1+⋯+Xn))=1n2D⁡(X1+⋯+Xn)=nσ2n2=σ2n.{\displaystyle \operatorname {D} ({\overline {X}}_{n})=\operatorname {D} ({\tfrac {1}{n}}(X_{1}+\cdots +X_{n}))={\frac {1}{n^{2}}}\operatorname {D} (X_{1}+\cdots +X_{n})={\frac {n\sigma ^{2}}{n^{2}}}={\frac {\sigma ^{2}}{n}}.}

Математическое ожидание последовательности μ{\displaystyle \mu } представляет собой среднее значение выборочного среднего:

E(X¯n)=μ.{\displaystyle \mathbb {E} ({\overline {X}}_{n})=\mu .}

Используя неравенство Чебышёва для X¯n{\displaystyle {\overline {X}}_{n}}, получаем

P⁡(|X¯n−μ|⩾ε)⩽σ2nε2.{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geqslant \varepsilon )\leqslant {\frac {\sigma ^{2}}{n\varepsilon ^{2}}}.}

Это неравенство используем для получения следующего:

P⁡(|X¯n−μ|<ε)=1−P⁡(|X¯n−μ|⩾ε)⩾1−σ2nε2,{\displaystyle \operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|<\varepsilon )=1-\operatorname {P} (\left|{\overline {X}}_{n}-\mu \right|\geqslant \varepsilon )\geqslant 1-{\frac {\sigma ^{2}}{n\varepsilon ^{2}}},}

при n→∞{\displaystyle n\rightarrow \infty }, выражение стремится к 1{\displaystyle {\mathit {1}}},

теперь по определению сходимости по вероятности мы получим:

X¯n →P μ{\displaystyle {\overline {X}}_{n}\ {\xrightarrow {P}}\ \mu }, при n→∞{\displaystyle n\rightarrow \infty }.

Доказательство с использованием сходимости характеристических функций

По теореме Тейлора для комплексных функций, характеристическая функция любой случайной величины X{\displaystyle X} с конечным средним μ{\displaystyle \mu } может быть записана как

φX(t)=1+itμ+o(t),t→{\displaystyle \varphi _{X}(t)=1+it\mu +o(t),\quad t\rightarrow 0.}

Все X1,X2,…{\displaystyle X_{1},X_{2},…} имеют одну и ту же характеристическую функцию, обозначим её как φX{\displaystyle \varphi _{X}}.

Среди основных свойств характеристических функций выделим два свойства

φ1nX(t)=φX(tn){\displaystyle \varphi _{{\frac {1}{n}}X}(t)=\varphi _{X}({\tfrac {t}{n}})} и φX+Y(t)=φX(t)φY(t){\displaystyle \varphi _{X+Y}(t)=\varphi _{X}(t)\varphi _{Y}(t)}, X{\displaystyle X} и Y{\displaystyle Y}независимы

Эти правила могут быть использованы для вычисления характеристической функции X¯n{\displaystyle {\overline {X}}_{n}} в терминах φX{\displaystyle \varphi _{X}}

φX¯n(t)=φX(tn)n=1+iμtn+o(tn)n→eitμ,{\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left^{n}=\left^{n}\,\rightarrow \,e^{it\mu },} при n→∞.{\displaystyle n\rightarrow \infty .}

Предел eitμ{\displaystyle e^{it\mu }}является характеристической функцией константы μ{\displaystyle \mu } и, следовательно, по теореме непрерывности Леви, X¯n{\displaystyle {\overline {X}}_{n}}сходится по распределению к μ{\displaystyle \mu }:

X¯n→Dμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {D}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Поскольку μ{\displaystyle \mu }- константа, то отсюда следует, что сходимость по распределению к μ{\displaystyle \mu } и сходимость по вероятности к μ{\displaystyle \mu } эквивалентны. Поэтому,

X¯n→Pμ{\displaystyle {\overline {X}}_{n}\,{\xrightarrow {\mathcal {P}}}\,\mu }, при n→∞.{\displaystyle n\to \infty .}

Это показывает, что среднее значение выборки по вероятности сходится к производной характеристической функции в начале координат, если она существует.

Куда лететь в отпуск и встречу ли я динозавра?

Структура общего решения линейного неоднородного дифференциального уравнения (ДУ). Метод Лагранжа. Метод Лагранжа (Метод вариации произвольных постоянных(МВПП)). 2) Согласно методу вариации произвольных постоянных (Лагранжа), решение уравнения (1) отыскивается в виде (3), в котором и — новые неизвестные функции. Сходимость называется сходимостью последовательности функции распределения к функции распределения или слабой сходимостью последовательности СВ к СВ : для слабой сходимости. Статистические гипотезы относительно неизвестных значений параметров распределения называют параметрическими, все другие гипотезы называются непараметрическими.

И в заключение известный вопрос о вероятности встретить на улице динозавра. Вы за жизнь провели 10 тысяч экспериментов – выходили на улицу и динозавра не встретили. Вероятность встретить динозавра, следовательно, близка к нулю, и нет особых оснований предполагать, что сегодня, выйдя на улицу в 10001 раз, вы его встретите.

Решение.Пусть случайная величинаX– срок службы мотора. Бернулли без доказательства.

Если первый раз герб выпадет при r-ом подбрасывании, r = 1, 2,…, m, игрок получает за партию 2r рублей. Согласно теореме 2, т.е. То есть почти всегда прибыль организаторов игры при взносе А=m мало отличается от нуля (в ту и другую сторону), если число сыгранных партий n велико. Этот результат не зависит от того, постоянно число подбрасываний m в каждой партии или может меняться по желанию игроков.

Рассмотрим пример: пусть вероятность поступления заказа в магазин А равна 0,2 или каждый 5-й звонящий делает заказ. Составим закон распределения поступления 5-ти заказов. Из графика (рис.2) можно увидеть, что вероятность поступления 3-х заказов составляет чуть больше 0,05, а 4-х и 5-ти — очень низкая. Числа 3, 4, 5 будут выпадать очень редко. Число 5 — практически невозможное событие.

Результат каждого опыта в отдельности случаен и непредсказуем, Так средний результат подчиняется закономерностям и предсказуем. Пусть Х — число «успехов» в схеме Бернулли с испытаниями, р — вероятность “успеха” в одном испытании. Он используется в тех случаях, когда неприменима схема случаев, т.е. нам неизвестна симметрия задачи.

Предположим, что в городе Н. предстоят выборы мэра, и число избирателей равно 100 тысячам. Более точным предсказание результата окажется при случайном отборе 1000 человек, и т.д.

Как и любой математический закон, закон больших чисел может быть применим к реальному миру только при известных допущениях, которые могут выполняться лишь с некоторой степенью точности. Так, например, условия последовательных испытаний часто не могут сохраняться бесконечно долго и с абсолютной точностью.

Он же впервые употребил термин «закон больших чисел». Теорему примем без доказательства. Маркову и крупным советским ученым С. Н. Бернштейну и А. Я. Хинчину.

Дополнительные статьи

Частота

Частота это число, которое показывает сколько раз в выборке встречается тот или иной элемент.

Предположим, что в школе проходят соревнования по подтягиваниям. В соревнованиях участвует 36 школьников. Составим таблицу в которую будем заносить число подтягиваний, а также число участников, которые выполнили столько подтягиваний.

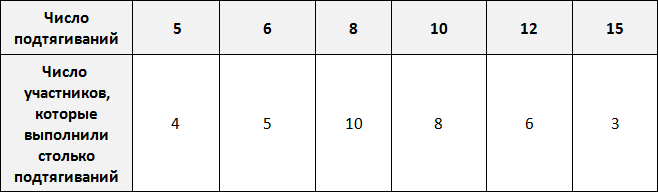
По таблице можно узнать сколько человек выполнило 5, 10 или 15 подтягиваний. Так, 5 подтягиваний выполнили четыре человека, 10 подтягиваний выполнили восемь человек, 15 подтягиваний выполнили три человека.

Количество человек, повторяющих одно и то же число подтягиваний в данном случае являются частотой. Поэтому вторую строку таблицы переименуем в название «частота»:

Такие таблицы называют таблицами частот.

Частота обладает следующим свойством: сумма частот равна общему числу данных в выборке.

Это означает, что сумма частот равна общему числу школьников, участвующих в соревнованиях, то есть тридцати шести. Проверим так ли это. Сложим частоты, приведенные в таблице:

4 + 5 + 10 + 8 + 6 + 3 = 36

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Ограничение

Среднее значение результатов, полученных в результате большого количества испытаний, в некоторых случаях может не совпадать. Например, среднее значение n результатов, взятых из распределения Коши или некоторых распределений Парето (α <1), не будет сходиться при увеличении n ; Причина — тяжелые хвосты . Распределение Коши и распределение Парето представляют два случая: распределение Коши не имеет математического ожидания, тогда как математическое ожидание распределения Парето (α <1) бесконечно. Другой пример: случайные числа равны касательной к углу, равномерно распределенному между -90 ° и + 90 °. Медиана равна нулю, но ожидаемое значение не существует, и на самом деле среднее значение п такие переменные имеют такое же распределение , как одной такой переменной. Оно не сходится по вероятности к нулю (или любому другому значению), когда n стремится к бесконечности.

Примеры

Например, один бросок правильной шестигранной кости дает одно из чисел 1, 2, 3, 4, 5 или 6, каждое с равной вероятностью . Таким образом, ожидаемое значение среднего бросков составляет:

1+2+3+4+5+66знак равно3.5{\ displaystyle {\ frac {1 + 2 + 3 + 4 + 5 + 6} {6}} = 3,5}

Согласно закону больших чисел, если бросается большое количество шестигранных игральных костей, среднее из их значений (иногда называемое выборочным средним ), вероятно, будет близко к 3,5, причем точность возрастает по мере того, как бросается больше кубиков.

Из закона больших чисел следует, что эмпирическая вероятность успеха в серии испытаний Бернулли будет сходиться с теоретической вероятностью. Для случайной величины Бернулли ожидаемое значение — это теоретическая вероятность успеха, а среднее значение n таких переменных (при условии, что они независимы и одинаково распределены (iid) ) — это именно относительная частота.

Например, справедливое подбрасывание монеты — это испытание Бернулли. Когда справедливая монета переворачивается раз, теоретическая вероятность того, что результат будет головки равен 1 / ₂ . Таким образом, в соответствии с законом больших чисел, доля голов в «большом» количестве бросков монеты «должно быть» примерно 1 / ₂ . В частности, доля головок после п переворачивает будет почти наверняка сходится к 1 / ₂ , как п стремится к бесконечности.

Хотя пропорция орла (и решки) приближается к 1/2, почти наверняка абсолютная разница в количестве орлов и решек станет большой по мере того, как количество флипов становится большим. То есть вероятность того, что абсолютная разница является малым числом, приближается к нулю, когда количество переворотов становится большим. Кроме того, почти наверняка отношение абсолютной разницы к количеству флипов будет приближаться к нулю. Интуитивно ожидаемая разница растет, но медленнее, чем количество переворотов.

Еще один хороший пример LLN — метод Монте-Карло . Эти методы представляют собой широкий класс вычислительных алгоритмов, которые полагаются на повторную случайную выборку для получения численных результатов. Чем больше количество повторений, тем лучше приближение. Причина, по которой этот метод важен, в основном состоит в том, что иногда трудно или невозможно использовать другие подходы.

Относительная частота

Относительная частота это в принципе та же самая частота, которая была рассмотрена ранее, но только выраженная в процентах.

Относительная частота равна отношению частоты на общее число элементов выборки.

Вернемся к нашей таблице:

Пять подтягиваний выполнили 4 человека из 36. Шесть подтягиваний выполнили 5 человек из 36. Восемь подтягиваний выполнили 10 человек из 36 и так далее. Давайте заполним таблицу с помощью таких отношений:

Выполним деление в этих дробях:

Выразим эти частоты в процентах. Для этого умножим их на 100. Умножение на 100 удобно выполнить передвижением запятой на две цифры вправо:

Теперь можно сказать, что пять подтягиваний выполнили 11% участников, 6 подтягиваний выполнили 14% участников, 8 подтягиваний выполнили 28% участников и так далее.

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Мода и медиана

Модой называют элемент, который встречается в выборке чаще других.

Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров

Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.

Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат

Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.

Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.

Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:

Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 183, 184, 185, 188, 190

В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.

Медианой упорядоченной выборки называют элемент, располагающийся посередине.

Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.

В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану

Но возможны случаи, когда количество элементов выборки чётно.

К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:

Построим этих шестерых спортсменов по росту:

Выпишем рост спортсменов отдельно:

180, 182, 184, 186, 188, 190

В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.

В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.

Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186

Найдем среднее арифметическое элементов 184 и 186

Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.

Поэтому более точное определение медианы зависит от количества элементов в выборке.

Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.

Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.

Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190

Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:

Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:

0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1

Определим среднее арифметическое для данной выборки — получим значение 2,2

По данному значению можно сказать, что в среднем у спортсменов 2,2 очка

Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:

0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6

В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.