Загадки на логику для детей: 100 занимательных задач

В словаре Д.Н. Ушакова

ЗАДА́ЧА, задачи, ·жен.1. Вопрос, требующий разрешения, то, что задано для решения, разрешения. Неразрешимая задача для философа.| Математический вопрос, для разрешения которого требуется путем вычислений найти какие-нибудь величины (мат.). Арифметическая, алгебраическая задача. Задачи на правило процентов.2. Цель; то, что необходимо осуществить, чего необходимо достигнуть; поручение, как заданная кому-нибудь цель. «Вслед за задачами военными встает задача хозяйственная.» Ленин. Задача построения фундамента социалистической экономики выполнена. Задача построить внеклассовое социалистическое общество — основная политическая задача второй пятилетки. Ставить себе, перед собой задачу. Иметь что-нибудь своей задачей. Задача сводится к чему-нибудь, к тому, чтобы… (см. сводиться» title=’что такое сводиться, значение слова сводиться в словаре Ушакова’>сводиться). «Задай лишь мне задачу: без дела, знаешь, от тебя не должен отлучиться я.» Пушкин.3. Удача, успех, счастье; ант. незадача (·обл. ). «Во всем-то ему задача, что дивится народ даже.» Л.Толстой.

Логика — это вкусняшка для ума

Именно так написали на доске ученики перед началом одного из занятий нашего кружка по логике. В чём же прелесть логических задач?

• они будут одинаково интересны и увлечённым математикой детям, и «гуманитариям»;
• многие из них не требуют знаний школьной программы;
• их может решать даже дошкольник без навыков чтения (например, судоку, ребусы, головоломки со спичками, «шестерёнки» и другие задачи в картинках).

Только системный и комплексный подход создаёт благоприятные предпосылки для формирования нестандартного мышления. «Пища для ума» тоже должна быть сбалансированной и разнообразной. Попробуйте сами и предложите вашим детям решить именно такую подборку задач. Это поможет выявить те звенья в логике, над которыми стоит поработать усерднее.

Задача про хитрого электрика

Одна­жды в сек­рет­ном каби­не­те что-то слу­чи­лось с про­вод­кой, и охра­на вызва­ла элек­три­ка, что­бы он всё почи­нил. Ему ска­за­ли, что три выклю­ча­те­ля нахо­дят­ся сна­ру­жи, а три лам­поч­ки — внут­ри. Лам­поч­ки сей­час не горят. Каж­дый выклю­ча­тель отве­ча­ет толь­ко за свою лам­поч­ку, но точ­ной схе­мы не зна­ет никто.

Элек­три­ку ска­за­ли как угод­но щёл­кать выклю­ча­те­ля­ми сна­ру­жи, но внутрь зай­ти раз­ре­ши­ли толь­ко один раз. Внут­ри с лам­поч­ка­ми тоже мож­но было делать что угод­но, но по сооб­ра­же­ни­ям сек­рет­но­сти воз­вра­щать­ся к выклю­ча­те­лям уже нель­зя. Элек­трик ухмыль­нул­ся, пощёл­кал выклю­ча­те­ля­ми, зашёл в ком­на­ту и сра­зу ска­зал, какой выклю­ча­тель отве­ча­ет за каж­дую лам­поч­ку. Как он это сде­лал?

Решение

Если решать зада­чу в лоб, то сра­зу напра­ши­ва­ет­ся такое реше­ние: вклю­чить одну лам­пу и выклю­чить дру­гую. В ито­ге, когда мы зай­дём в ком­на­ту, одна будет гореть, а дру­гая — нет, и мы пой­мём, какой выклю­ча­тель за что отве­ча­ет.

Но что делать с тре­тьей лам­пой? Если мы вклю­чим и её, то как отли­чим от такой же пер­вой? А если выклю­чим, то как отли­чим от нера­бо­та­ю­щей вто­рой? Нуж­но научить­ся раз­ли­чать две оди­на­ко­вые рабо­та­ю­щие или нера­бо­та­ю­щие лам­пы.

Самый про­стой спо­соб это сде­лать — раз­де­лить сами лам­пы допол­ни­тель­но на тёп­лые и холод­ные. Лам­па ста­но­вит­ся тёп­лой, когда пора­бо­та­ет, и даже если её выклю­чить, она всё рав­но какое-то вре­мя оста­нет­ся тёп­лой.

По усло­вию мы зна­ем, что все три лам­пы выклю­че­ны. Но вдруг они недав­но вклю­ча­лись и ещё не успе­ли остыть? Зна­чит, пер­вое, что мы дела­ем, — ждём неко­то­рое вре­мя, что­бы все лам­пы осты­ли.

Теперь щёл­ка­ем любым выклю­ча­те­лем и нагре­ва­ем одну лам­пу. После того, как она пора­бо­та­ла доста­точ­но вре­ме­ни, что­бы нагреть­ся, мы её выклю­ча­ем. Полу­ча­ет­ся, что у нас все три лам­пы выклю­че­ны, но две из них холод­ные, а одна — тёп­лая.

Затем, что­бы раз­ли­чить две холод­ные лам­пы, щёл­ка­ем любым дру­гим выклю­ча­те­лем и захо­дим в ком­на­ту. В ито­ге мы уви­дим:

• одну рабо­та­ю­щую лам­поч­ку, кото­рую мы вклю­чи­ли толь­ко что;
• одну нера­бо­та­ю­щую, но тёп­лую лам­поч­ку, кото­рую мы нагре­ли до это­го;
• и одну нера­бо­та­ю­щую и холод­ную лам­поч­ку, выклю­ча­тель от кото­рой мы ни разу не тро­га­ли.

Теп­ло и логи­ка!

Загадки

1. Вор вошёл в хорошо охраняемое здание, не потревожив сигнализацию, и его не задержала охрана. Он пробыл там длительное время и беспрепятственно вышел. Если бы он пробыл в этом здании хотя бы немного меньше, его бы задержали. Где был вор?

2. Человек стрелял в зайца, а домой принес медведя. Как так?

3. Не раз привлекавшийся к суду Эдди по кличке «Одноглазый» был задержан ночью за нарушение порядка. На следующее утро в этом же городе в прихожей собственной квартиры был обнаружен труп вдовы Бремер. Инспектор вызвал на допрос одноглазого Эдди, который заявил, что вечером он действительно побывал у некоторых своих «клиентов». На вопрос инспектора, принадлежала ли к числу его «клиентов» вдова Бремер, Эдди заявил, что смерть вдовы к нему не имеет отношения. Тогда инспектор спросил его, откуда он знает о смерти вдовы. Эдди ответил, что, проходя мимо ее дома, заглянул в замочную скважину и увидел ее лежащей на полу. Он позвонил, но на звонок никто не вышел. После осмотра квартиры вдовы инспектор приказал арестовать Эдди.

Как инспектор понял, что Эдди врет?

Загадки

9

Примите жизненно важное решение. В комнате без света есть три двери: за первой спряталась ядовитая змея, за второй – лев, который не ел пару дней, в третьей вас ждет экзекуция на электрическом столе

Какую дверь безопаснее всего открыть?

10. Разминка на логику и память. В названии какого города спрятались имена ста девушек и одного парня?

11. Логическая загадка: у отца Фрэнка 5 сыновей. Имена его четырех сыновей — Фефе, Фифи, Фофо, Фуфу. Соответственно, как зовут его пятого сына?

12. Знаменитая загадка: по пути в Сент-Айвз я увидел мужчину с 7 женами. У каждой жены было 7 мешков. В каждом мешке было по 7 кошек. У каждого кота было 7 котят. Котенок, кошки, мешки, жены – сколько их направляются в Сент-Айвс?

Функции и цели общения

Существует три функции общения:

• регулятивная – изменение поведения одним лицом у другого (например, начальник дает подчиненному какое-либо распоряжение);
• информационная – передача информации друг другу;
• аффективная – взаимообмен эмоциями.

Цели общения можно подразделить на функциональные и объектные.

К функциональным целям общения относится:

• изменение мнения, намерения, поведения другого человека;
• поиск человека, который может дать поддержку, похвалу, сочувствие, понимание, эмоциональный отклик;
• оказание помощи другому человеку;
• получение помощи;
• самовыражение (общение с теми, кто дает возможность проявить свои умения, находчивость, смекалку, способности);
• поиск партнера для совместной деятельности, беседы, игры и так далее (т. е. партнера для взаимодействия);
• приобщение другого (других) к своим или общечеловеческим ценностям (воспитание, обучение).

Готовые работы на аналогичную тему

• Курсовая работа Цели общения в психологии 480 руб.
• Реферат Цели общения в психологии 270 руб.
• Контрольная работа Цели общения в психологии 200 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость К объектным целям общения относится поиск собеседника – человека, который может дать именно то, что нужно.

Что касается функций общения, их можно подразделить на следующие типы:

• информационная;
• экспрессивная;
• регулятивная;
• социализации;
• социального контроля.

Советский психолог Борис Федорович Ломов выделяет также другие функции общения, которые другими специалистами определяются как цели общения. К ним относится:

• устанавливание и развитие межличностных отношений;
• организация совместной деятельности;
• познание личностных особенностей собеседника.

Если рассматривать общепринятые функции общения, то информационная отвечает за прием и передачу информации от одного человека к другому. Экспрессивная функция отвечает за перенимание эмоционального состояния другого человека, т.к. часто человек нуждается в общении для того, чтобы изменить свое эмоциональное состояние. Регулятивная функция нужна для того, чтобы воздействовать на участника межличностного общения для того, чтобы изменить его поведение в лучшую сторону, однако это воздействие обязательно должно быть обоюдным. Функция социализации важна по причине формирования единого целого в коллективе. Для успешного «выживания» необходимо учитывать интересы других, выражать доброжелательность, производить действия, направленные на улучшение отношений в коллективе. Функция социального контроля отвечает за установления норм поведения и наказаний за их несоблюдение.

Лень читать?

Задай вопрос специалистам и получи ответ уже через 15 минут!

Задать вопрос

Загадки на логику для детей 7-8 лет

Загадки на логику для детей 7-8 лет это загадки для первоклассников, которые уже учатся в школе.Загадка №50

В зоопарке живёт столько жёлтых попугаев, сколько и голубых.Голубых столько же, сколько и красных. Посчитай, сколько всего попугаев, если красных три.

(Ответ: Всего попугаев 9. Жёлтые = голубые. Голубые = красные. Красные = 3. 3 красных + 3 голубых + 3 желтых = 9.)

***

Загадка №51

Вася, Гоша и Витя едят мороженое. Ребята поедают эскимо, фруктовый лёд, и пломбир в вафельном стаканчике. Догадайся, кто какое мороженое ест, если известно, что Вася не любит эскимо, а Витя лакомится фруктовым льдом.

(Ответ: Вася, Гоша и Витя едят мороженое. Ребята поедают эскимо, фруктовый лёд, и пломбир в вафельном стаканчике. Догадайся, кто какое мороженое ест, если известно, что Вася не любит эскимо, а Витя лакомится фруктовым льдом.)

***

Загадка №52

Что делает сторож, когда у него на шапке сидит воробей?

(Ответ: Спит)

***

Загадка №53

Бежит без ног, не зная горя, И добирается до моря.

(Ответ: Река)

***

Загадка №54

В воде она живет, Нет клюва, а клюет.

(Ответ: Рыба)

***

Загадка №55

Три, три, три и три…Что будет?

(Ответ: Дырка)

***

Загадка №56

Накормишь – живет, Напоишь – умрет.

(Ответ: Огонь)

***

Загадка №57

Гусеница не длиннее червяка. Червяк не длиннее гусеницы. Кто длиннее?

(Ответ: Одинаковые)

***

Загадка №58

У бабушки Ани внук Сережа, кот Пушок, собака Бобик. Сколько у бабушки внуков?

(Ответ: Один)

***

Загадка №59

Какой прибор человек перед сном включает, а утром выключает?

(Ответ: Будильник)

***

Загадка №60

Как отыскать черную кошку в комнате, где выключен свет?

(Ответ: Включить свет)

***

Загадка №61

У бабушки живут три кошки – кошка Мурка, кошка Клава и кошка Лиза. Обычно они спят на трех разных подушках – желтой, розовой и синей. Кошка Клава любит спать на розовой подушке. Кошка Мурка никогда не выбирает ни розовую, ни синюю. Подумай и скажи, на какой подушке должна спать каждая из кошек?

(Ответ: Клава – на розовой, Мурка – на желтой, Лиза – на синей.)

***

Загадка №62

Какое число уменьшится на треть, если его перевернуть?

(Ответ: 9)

***

Загадка №63

На дереве висело восемь яблок: три красных и пять зеленых. Через два дня покраснели еще два яблока. Сколько теперь яблок на дереве?

(Ответ: 8)

***

Загадка №64

За что обычно учеников выгоняют из класса?

(Ответ: За дверь)

***

Загадки с подвохом

Задача 7. Отгадайте, кому принадлежит кукла: у Леры и Рады куклы с голубыми волосами, а у Дины и Стаси – со светлыми. У Рады и Стаси куклы в платьях, а у Леры и Дины – в юбках и блузах.

Определите хозяйку каждой куклы.

Задача 8. Хитрая загадка: есть подвал, в котором находятся 3 лампочки. Выключатели от этих лампочек находятся вне подвала так, что даже при открытых дверях в подвал не видно, горят ли лампочки. Как, войдя всего 1 раз в подвал, определить, который из 3-х выключателей какой лампочке соответствует?

Задача 9. Математическая загадка: у Кристины есть 4 разных платья и 3 разных пары туфель. Она собирается на вечеринку и думает, что ей надеть. Сколько у Кристины вариантов образа?

Смышлёный малыш

Три брата получили 24 яблока, причём каждому досталось столько яблок, сколько ему было лет три года назад. Самый младший, мальчик очень смышлёный, предложил братьям такой обмен яблоками:

— Я, — сказал он, — оставлю себе только половину имеющихся у меня яблок, а остальные разделю между вами поровну. После этого пусть средний брат тоже оставит себе половину, а остальные яблоки даст мне и старшему брату поровну, а затем и старший брат пусть оставит себе половину всех имеющихся у него яблок, а остальные разделит между мной и средним братом поровну.

Братья, не подозревая коварства в таком предложении, согласились удовлетворить желание младшего. В результате… у всех оказалось яблок поровну. Сколько же лет было малышу и каждому из остальных братьев?

Показать ответ

Скрыть ответ

В конце обмена у каждого из братьев оказалось по 8 яблок. Следовательно, у старшего перед тем, как он отдал половину яблок своим братьям, было 16 яблок, а у среднего и младшего — по 4 яблока.

Далее, перед тем как делил свои яблоки средний брат, у него было 8 яблок, а у старшего — 14 яблок, у младшего — 2. Отсюда, перед тем как делил свои яблоки младший брат, у него оказалось 4 яблока, у среднего — 7 яблок и у старшего — 13.

Так как каждый получил вначале столько яблок, сколько ему было три года назад, то младшему сейчас 7 лет, среднему брату 10 лет, а старшему 16.

Математические задачи на логику для дошкольников

Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей

Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет

1. На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
2. Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.

3. Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.

   Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.

4. Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
5. Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
6. На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.
7. Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
8. У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.

9. Какие камни есть в море? Ответ: мокрые.

   Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.

10. Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
11. В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
12. Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
13. Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.
14. Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
15. Что все дети на земле делают одновременно? Ответ: взрослеют.

Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.

Возможные проблемы

Как не выйти замуж

Однажды хозяин мелкой лавки в Италии задолжал ростовщику крупную сумму. Возможности отдать долг у него не было. Зато была красавица‑дочь, которая давно нравилась кредитору.

Но девушка не хотела выходить замуж за старого и некрасивого мужчину. Поэтому лавочник ответил отказом. Однако потенциальный зять уловил в его голосе колебание и сделал новое предложение.

Сделка выглядела справедливой, и на этот раз отец согласился. Ростовщик наклонился к дорожке, усыпанной галькой, быстро поднял камни и положил их в мешочек. Но дочь заметила ужасное: оба камушка были чёрными! Какой бы она ни вытащила, ей пришлось бы выходить замуж. Конечно, можно было уличить ростовщика в обмане, вынув сразу оба камня. Но тот мог бы прийти в ярость и отменить сделку, затребовав долг в полном объёме.

Подумав пару секунд, девушка уверенно протянула руку к мешочку. И сделала кое‑что, что избавило её отца от долга, а её саму — от необходимости замужества. Справедливость её поступка признал даже ростовщик. Что именно она сделала?

Посмотреть ответ

Скрыть

Девушка вытащила камень и, не успев показать никому, будто случайно уронила его на дорожку. Камушек тут же смешался с остальной галькой.

Конечно же, когда все заглянули в мешок, там обнаружился чёрный камень. Даже ростовщик был вынужден согласиться: это означает, что девушка вытащила белый. А раз так — свадьбы не будет и долг придётся простить.

Посылки для повстанцев

Мария отвечает за поставку важных ресурсов на базу повстанцев, которая расположена в самом сердце вражеской территории. На таможне все посылки проверяют по чёткому протоколу: если на дне коробки стоит чётное число, её нужно запечатать красной крышкой.

Партию коробок уже начали загружать в транспорт, когда Мария получила срочное сообщение: одна из четырёх коробок помечена неправильно, но какая именно — неизвестно.

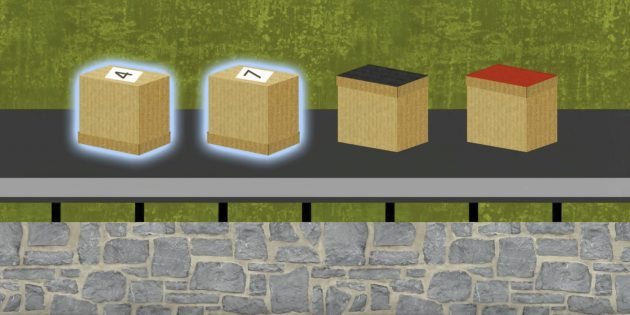
Коробки всё ещё на конвейерной ленте. Две стоят дном вверх: на одной указана цифра 4, на второй — цифра 7. Две другие коробки стоят дном вниз: у одной чёрная крышка, у второй — красная.

YouTube-канал TED-Ed

Мария знает, что из-за любого нарушения протокола партию конфискуют, а её союзники окажутся в смертельной опасности

Взяв коробку на проверку, девушка уже не сможет вернуть её на конвейер и лишит мятежников жизненно важной поставки. Транспорт скоро отправляется — с грузом или без него

Какую коробку или коробки нужно снять с конвейерной ленты?

Посмотреть решение

Скрыть решение

Сначала кажется, что нужно проверить обратную сторону каждой коробки, но на самом деле Марии нужны только две.

Чтобы понять, в чём разгадка, вернёмся к протоколу. Там говорится, что у коробок с чётными числами должна быть красная крышка. О коробках с нечётными числами там не сказано ни слова, поэтому пропускаем коробку с цифрой 7.

А как же коробка с красной крышкой? Разве не нужно проверить число у неё на дне? Получается, что нет. Согласно протоколу, у коробок с чётными числами на дне должна быть красная крышка. Это не значит, что красная крышка может быть только у коробок с чётным числом или что коробки с красной крышкой обязательно помечены чётным числом. Требование здесь одностороннее, поэтому не нужно проверять коробку с красной крышкой.

Однако нужно проверить коробку с чёрной крышкой, чтобы убедиться, что ей по ошибке не накрыли коробку с чётным числом. Значит, Марии нужно снять с конвейера две коробки: ту, на которой написана цифра 4, и ту, у которой чёрная крышка.

Если вы подумали, что красные крышки могут быть только на коробках с чётными числами, вы не одиноки. Это заблуждение встречается настолько часто, что даже получило название «ошибка утверждения следствия».

Её суть в следующем: определённое условие является не только необходимым для конкретного результата, но и достаточным. Например, наличие атмосферы необходимо, чтобы планета была пригодна для жизни. Но это условие не является достаточным. Например, у Венеры есть атмосфера, но это не делает её пригодной для жизни.

Отзывы

Новые приключения хитрого электрика

Один про­вай­дер решил про­ве­сти интер­нет через реку — от лево­го бере­га до пра­во­го. Для это­го он под водой про­ло­жил 49 про­во­дов, по кото­рым пере­да­ют­ся сиг­на­лы и элек­три­че­ский ток.

Все про­во­да ока­за­лись оди­на­ко­во­го цве­та, а под­ряд­чик забыл про­мар­ки­ро­вать их, что­бы понять, где какие кон­цы про­во­дов на обо­их бере­гах.

Что­бы выяс­нить, где что, позва­ли элек­три­ка и ска­за­ли ему под­пи­сать все про­во­да чис­ла­ми от 1 до 49 с каж­дой сто­ро­ны. Его зада­ча — про­ну­ме­ро­вать про­во­да на левом бере­гу и на пра­вом, разу­ме­ет­ся, что­бы чис­ла сов­па­ли.

Ему предо­ста­ви­ли катер, кото­рый может возить его сколь­ко угод­но раз с одно­го бере­га на дру­гой, линию с током на исход­ном бере­гу и муль­ти­метр, кото­рый пока­зы­ва­ет напря­же­ние в про­во­де.

Все дума­ли, что элек­трик пере­се­чёт реку как мини­мум 49 раз, но ему хва­ти­ло все­го двух раз — туда и обрат­но. Потом он про­сто сидел на бере­гу и задум­чи­во смот­рел на воду. Как ему это уда­лось?

Решение

На исход­ном бере­гу элек­трик пода­ёт напря­же­ние на любой про­вод и поме­ча­ет его как № 1. Все осталь­ные 48 он попар­но соеди­ня­ет меж­ду собой, что­бы на этой сто­роне полу­чил­ся один про­вод под напря­же­ни­ем и 24 пары. Как он это дела­ет — вооб­ще не важ­но, поря­док пар сей­час роли не игра­ет. После это­го элек­трик отправ­ля­ет­ся на пра­вый берег (пер­вая поезд­ка).

При­плыв на место, он нахо­дит про­вод под напря­же­ни­ем с помо­щью тесте­ра — это про­вод № 1, он его так и поме­ча­ет. А даль­ше начи­на­ет­ся элек­три­че­ская магия.

Элек­трик берёт про­вод № 1 под напря­же­ни­ем, соеди­ня­ет его с любым дру­гим про­во­дом и под­пи­сы­ва­ет его как № 2. Но мы пом­ним, что на левом бере­гу все про­во­да соеди­не­ны попар­но, зна­чит, про­вод № 2 с той сто­ро­ны тоже с чем-то соеди­нён, а зна­чит, ток вер­нёт­ся обрат­но и появит­ся в новом про­во­де, кото­рый элек­трик под­пи­шет как № 3.

Даль­ше всё то же самое: он берёт про­вод с током № 3, соеди­ня­ет его с любым остав­шим­ся про­во­дом и под­пи­сы­ва­ет новый про­вод как № 4. А ещё он пом­нит про пары на том бере­гу, поэто­му ищет про­вод, в кото­ром сно­ва появил­ся ток и под­пи­сы­ва­ет его как № 5. Таким же обра­зом он соеди­ня­ет остав­ши­е­ся про­во­да и нуме­ру­ет все жилы на пра­вой сто­роне от 1 до 49. Сде­лав это, элек­трик воз­вра­ща­ет­ся на левый берег (вто­рая поезд­ка).

Оста­лось самое инте­рес­ное: как на этом бере­гу про­ста­вить те же самые чис­ла на про­во­дах. Элек­трик зна­ет, как выгля­дит про­вод № 1, пото­му что он его под­пи­сал, но не зна­ет, как выгля­дит про­вод № 2.

Но он пом­нит, что про­вод № 1 соеди­нён на том бере­гу с про­во­дом № 2, кото­рый на этом бере­гу соеди­нён с про­во­дом № 3. Зна­чит, зада­ча элек­три­ка в том, что­бы най­ти это соеди­не­ние на левом бере­гу, где он нахо­дит­ся. Для это­го он разъ­еди­ня­ет по оче­ре­ди все соеди­не­ния и смот­рит, про­пал ли ток во всех осталь­ных про­во­дах. Если не про­пал во всех осталь­ных — зна­чит, разъ­еди­нил не ту пару и воз­вра­ща­ет её на место. А если про­пал — зна­чит, элек­трик нашёл соеди­не­ние про­во­дов № 2 и № 3. При этом тот неиз­вест­ный про­вод, кото­рый остал­ся под напря­же­ни­ем, будет про­вод № 2, а тот, с кото­рым он соеди­нял­ся, будет № 3.

После это­го элек­трик соеди­ня­ет под­пи­сан­ную пару обрат­но и начи­на­ет искать сле­ду­ю­щую точ­ку, кото­рая отклю­ча­ет все осталь­ные жилы — это будут про­во­да № 4 и № 5. Дей­ствуя по этой схе­ме, хит­рый элек­трик под­пи­шет все остав­ши­е­ся про­во­да. Про­вай­де­ру оста­нет­ся толь­ко разъ­еди­нить пары на каж­дом бере­гу.

Система подсказок

Чтобы оптимально активизировать мыслительную деятельность обучающихся, рекомендуется использовать дидактический приём под названием «Система подсказок». Данная техника состоит из второстепенных заданий или вопросов, что придают правильное направление мыслительному потоку, делая поиск решения упорядоченным. Решение заданий требует наличия комбинационных способностей, то есть умений делать правильный выбор в условиях перенасыщенности знаний. Этот поиск и подбор должен быть целенаправленным. Выбор будет осуществляться гораздо быстрее и легче, если обратиться к подходящей аналогии. Например, можно задать вопрос: «Где ранее встречалось что-то похожее?» Используя метод аналогии при решении заданий, рекомендуется изменять их формулировку. Применять эту технику лучше всего на начальной стадии решения задач. Если именно здесь удается сравнить данное задание с теми, что решались ранее, то сходство условий и методов решения направляет обучающихся на правильный путь, развивает появление плодотворных идей при составлении плана решения.

График мероприятий

Олимпиады и конкурсы составлены высококвалифицированными преподавателями, которые разработали и провели более тысячи различных мероприятий В мероприятиях участвуют тысячи учащихся школ, лицеев, гимназий, училищ, образовательных центров, детских садов, что обеспечивает всероссийский масштаб Вас ожидают интересные, разнообразные, увлекательные и творческие задания Участники: развивают свои интеллектуальные способности, логику и мышление проверяют, закрепляют и систематизируют знания по главным предметам узнают результат и получают дипломы победителей или сертификаты участников в течение 5 дней со дня получения нами работы Учителя получают сертификаты куратора и благодарственные письма Мы компенсируем затраты кураторов на печать заданий для участников (при пополнении счёта от 1000 руб.) Вы пополняете свои портфолио новыми наградами Мы официально зарегистрированы в Роскомнадзоре и имеем Свидетельство СМИ ЭЛ № ФС77-67689 от 10.11.2016

Как принять участие в мероприятии

Уважаемые педагоги, школьники и родители! Если вы решили участвовать в наших дистанционных школьных олимпиадах, конкурсах или викторинах, вам необходимо сделать всего несколько шагов:

1. Ознакомьтесь с правилами участия и договором-офертой.
2. Зарегистрируйтесь на нашем сайте и войдите в личный кабинет.
3. Заполните список участников.
4. Создайте заявку на участие в творческом конкурсе или интеллектуальной олимпиаде.
5. Оплатите заявку со счета на сайте.

Как пополнить счёт на сайте:
Создайте заявку на пополнение вашего счёта на сайте в разделе все заявки.
Оплатите заявку на пополнение счёта в банке или с помощью ROBOKASSA (инструкция по оплате).
После пополнения счета самостоятельно оплатите заявки на участие в мероприятии.

После оплаты заявки на участие в мероприятии в личном кабинете размещаются задания выбранной школьной олимпиады, конкурса или викторины (при наличии таких заданий).
После выполнения заданий дистанционного мероприятия участник или куратор в установленные сроки и в установленном формате загружает работы для проверки через специальную форму, доступную из созданной заявки.

Участники мероприятия:
В дистанционном мероприятии могут принять участие ученики школ, образовательных центров, лицеев, гимназий, колледжей и других образовательных учреждений.

Уважаемые педагоги и школьники!
Участвуйте в наших всероссийских дистанционных школьных олимпиадах, конкурсах и викторинах! Это блестящая возможность постигнуть очередную ступень саморазвития и пополнить свои портфолио!

Как рассадить интровертов в баре

А вот задач­ка на струк­ту­ры дан­ных, сор­ти­ров­ку и алго­рит­ми­ку, кото­рая воз­мож­на толь­ко в нашей стране.

В Петер­бур­ге на ули­це Рубин­штей­на есть один бар, в кото­рый ходят лишь необ­щи­тель­ные люди, назо­вём их интро­вер­та­ми. (На самом деле интро­вер­ты общи­тель­ные, необ­щи­тель­ность — это миф. Но это задач­ка, поэто­му упро­стим.)

Интро­вер­ты садят­ся вдоль бар­ной стой­ки, где есть 25 мест. Когда вхо­дит новый посе­ти­тель, он все­гда садит­ся у стой­ки как мож­но даль­ше от осталь­ных гостей. Никто не садит­ся на сосед­нее место рядом с дру­гим интро­вер­том: если кто-то вхо­дит и видит, что сво­бод­ных мест мало и надо сесть рядом с кем-то, то он ухо­дит.

Бар­мен хочет полу­чить как мож­но боль­ше кли­ен­тов. У него есть пра­во поса­дить само­го пер­во­го посе­ти­те­ля на любое место у стой­ки. Куда выгод­нее поса­дить пер­во­го интро­вер­та с точ­ки зре­ния бар­ме­на?

Решение

Для нача­ла най­дём иде­аль­ный вари­ант, кото­рый устро­ил бы бар­ме­на. Для это­го нари­су­ем 25 квад­ра­тов в ряд и закра­сим те, на кото­рых кто-то сидит. Помни­те, что ни один интро­верт по зада­че не сядет на сосед­нее место к дру­го­му.

Полу­ча­ет­ся, что это самая плот­ная рас­сад­ка, кото­рая воз­мож­на в этом баре. Так у стой­ки сидят 13 чело­век. Оста­лось толь­ко най­ти место для само­го пер­во­го посе­ти­те­ля.

Для нача­ла попро­бу­ем решить эту зада­чу в лоб и поса­дим пер­во­го посе­ти­те­ля на пер­вый стул:

Теперь вто­рой посе­ти­тель дол­жен сесть на сво­бод­ное место как мож­но даль­ше от него, то есть занять стул № 25:

Тре­тье­му доста­ёт­ся стул № 13, так как он ров­но посе­ре­дине меж­ду эти­ми дву­мя:

Два сле­ду­ю­щих зай­мут сво­бод­ные места точ­но посе­ре­дине меж­ду цен­траль­ным и боко­вы­ми:

И вот тут наста­ёт момент исти­ны: четы­ре сле­ду­ю­щих посе­ти­те­ля тоже сядут точ­но посе­ре­дине меж­ду заня­ты­ми места­ми. Это зна­чит, что меж­ду каж­дым будет по 2 пустых места:

В ито­ге у нас заня­то все­го 9 мест, но сесть боль­ше нику­да нель­зя: у каж­до­го сво­бод­но­го сту­ла есть как мини­мум один заня­тый сосед. Зна­чит, этот вари­ант не под­хо­дит. Нужен дру­гой.

Что­бы прий­ти к пра­виль­но­му отве­ту, попро­бу­ем решать зада­чу с кон­ца.

Вспом­ним иде­аль­ную рас­сад­ку:

Здесь сидит мак­си­маль­ное коли­че­ство гостей — 13, и меж­ду каж­дым из них есть сво­бод­ное место. Отмо­та­ем на шаг назад и посмот­рим, как мог­ли бы сидеть интро­вер­ты, что­бы новые гости сели точ­но меж­ду ними:

В этом слу­чае 6 новых гостей садят­ся точ­но посе­ре­дине меж­ду заня­ты­ми сту­лья­ми и иде­аль­но запол­ня­ют все места.

Теперь сде­ла­ем ещё шаг назад и посмот­рим, как долж­ны сидеть гости, что­бы новые кли­ен­ты сели на нуж­ные сту­лья:

Полу­ча­ет­ся, что если мы поса­дим пер­вых четы­рёх гостей так, как на рисун­ке выше, то даль­ше всё будет хоро­шо. Сде­ла­ем ещё шаг назад, что­бы понять, как они смог­ли так сесть:

Из рисун­ка вид­но, что два новых посе­ти­те­ля долж­ны сесть как мож­но даль­ше от заня­тых мест. Для это­го один садит­ся ров­но посе­ре­дине меж­ду дву­мя заня­ты­ми, а вто­рой — с само­го края, на пер­вое место. Таким обра­зом, меж­ду все­ми ними будет мак­си­маль­но воз­мож­ное рас­сто­я­ние. Оста­лось понять, как сели эти пер­вые два интро­вер­та.

Если бы пер­вый гость сел с краю на стул № 25, вто­ро­му бы при­шлось сесть с про­ти­во­по­лож­но­го края на стул № 1 (мы это разо­бра­ли в самом нача­ле, в непра­виль­ном вари­ан­те). Зна­чит, пер­вый гость сел на стул № 9, а вто­ро­му при­шлось сесть мак­си­маль­но дале­ко от него — на самый послед­ний стул:

Полу­ча­ет­ся, само­го пер­во­го гостя бар­мен дол­жен поса­дить на стул № 9.

Как так вышло? Про­сто посчи­та­ли от обрат­но­го. Про­грам­ми­сты назы­ва­ют это Test-First Development, хех.

1) Метод графов.

Даны отношения между предметами и следуя по цепочке этих отношений, мы приходим к правильному результату. Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками. Рассмотрим метод графов на примере решения задачи.Задача “Любимые мультфильмы”: Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам?Решение.Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками.
Поэтому граф на рисунке будет выглядеть следующим образом:

Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. Поэтому нужно найти единственно возможное соответствие между элементами двух множеств.

Правилоесли какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной.
Поэтому граф на рисунке будет выглядеть следующим образом:

Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обеих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри».

Задача решена.2) Круги Эйлера. Второй способ, которым решаются такие задачи круги Эйлера – задачи на пересечение или объединение множеств.Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.