Методологическое сомнение в философии р. декарта

Прямоугольные координаты вектора

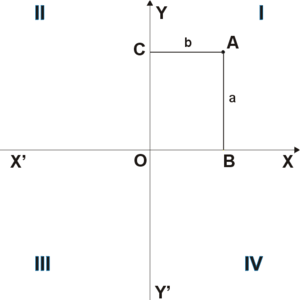
Рис. 1

Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца.

Таким образом, например, координаты (x,y){\displaystyle (x,y)} на рис.1 являются координатами вектора OA→{\displaystyle {\vec {OA}}}.

Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:

1. Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
2. Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.

Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.

В прямоугольных координатах очень просто записываются все операции над векторами:

Сложение и умножение на скаляр:

a+b=(a1+b1,a2+b2,a3+b3,…,an+bn){\displaystyle \mathbf {a} +\mathbf {b} =(a_{1}+b_{1},a_{2}+b_{2},a_{3}+b_{3},\dots ,a_{n}+b_{n})}

или

(a+b)i=ai+bi,{\displaystyle (\mathbf {a} +\mathbf {b} )_{i}=a_{i}+b_{i},}

c a=(c a1,c a2,c a3,…,c an){\displaystyle c\ \mathbf {a} =(c\ a_{1},c\ a_{2},c\ a_{3},\dots ,c\ a_{n})}

или

(c a)i=c ai.{\displaystyle (c\ \mathbf {a} )_{i}=c\ a_{i}.}

а отсюда и вычитание и деление на скаляр:

a−b=(a1−b1,a2−b2,a3−b3,…,an−bn){\displaystyle \mathbf {a} -\mathbf {b} =(a_{1}-b_{1},a_{2}-b_{2},a_{3}-b_{3},\dots ,a_{n}-b_{n})}

или

(a−b)i=ai−bi,{\displaystyle (\mathbf {a} -\mathbf {b} )_{i}=a_{i}-b_{i},}

aλ=(a1λ,a2λ,a3λ,…,anλ){\displaystyle {\frac {\mathbf {a} }{\lambda }}={\Big (}{\frac {a_{1}}{\lambda }},{\frac {a_{2}}{\lambda }},{\frac {a_{3}}{\lambda }},\dots ,{\frac {a_{n}}{\lambda }}{\Big )}}

или

(aλ)i=aiλ.{\displaystyle {\Big (}{\frac {\mathbf {a} }{\lambda }}{\Big )}_{i}={\frac {a_{i}}{\lambda }}.}

(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).

Скалярное произведение:

a⋅b=a1b1+a2b2+a3b3+⋯+anbn{\displaystyle \mathbf {a} \cdot \mathbf {b} =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}+\dots +a_{n}b_{n}}

или

a⋅b=∑i=1naibi,{\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum \limits _{i=1}^{n}a_{i}b_{i},}

(Только в прямоугольных координатах с единичным масштабом по всем осям).

Через скалярное произведение можно вычислить длину вектора

|a|=a⋅a{\displaystyle |\mathbf {a} |={\sqrt {\mathbf {a} \cdot \mathbf {a} }}}

и угол между векторами

∠(a,b)=arccosa⋅b|a|⋅|b|{\displaystyle \angle {(\mathbf {a} ,\mathbf {b} )}=\mathrm {arccos} {\frac {\mathbf {a} \cdot \mathbf {b} }{|\mathbf {a} |\cdot |\mathbf {b} |}}}

Внешнее произведение:

(a∧b)ij=aibj−ajbi{\displaystyle (\mathbf {a} \land \mathbf {b} )_{ij}=a_{i}b_{j}-a_{j}b_{i}}

для любой размерности пространства,

Векторное произведение (только для трехмерного же пространства, на котором оно и определено):

(a×b)x=aybz−azby{\displaystyle (\mathbf {a} \times \mathbf {b} )_{x}=a_{y}b_{z}-a_{z}b_{y}}

(a×b)y=azbx−axbz{\displaystyle (\mathbf {a} \times \mathbf {b} )_{y}=a_{z}b_{x}-a_{x}b_{z}}

(a×b)z=axby−aybx{\displaystyle (\mathbf {a} \times \mathbf {b} )_{z}=a_{x}b_{y}-a_{y}b_{x}}

Очевидно, всё это позволяет, если надо, свести все операции над векторами к достаточно простым операциям над числами.

Метод Декарта

Ученый полагал, что опыт необходим лишь для помощи разуму в тех ситуациях, когда прийти к истине исключительно размышлениями невозможно. Через всю научную жизнь Декарт пронес четыре основные составляющие метода поиска истины:

1. Начинать необходимо из наиболее очевидного, не подлежащего сомнениям. С того, противоположное чему даже невозможно допустить.
2. Любая проблема должна разделяться на столько мелких частей, сколько потребуется, чтобы добиться ее продуктивного решения.
3. Начинать следует с простого, от которого нужно постепенно передвигаться ко все более сложному.
4. На каждом этапе необходимо перепроверять правильность составленных умозаключений, чтобы по результатам исследования быть уверенным в объективности полученных знаний.

Исследователи отмечают, что эти правила, которые Декарт неизменно использовал, создавая труды, ярко демонстрируют стремление европейской культуры XVII века к отказу от устаревших правил и к построению новой, прогрессивной и объективной науки.

Скептицизм сделает вас счастливым (или нет)

Основоположник школы скептицизма Пиррон советовал всем, кто стремится к счастью, обратить внимание на три обстоятельства: во-первых, какова природа вещей; во-вторых, как следует к ним относиться; и в-третьих, к чему это должно привести. Вещи сами по себе, пишет Секст Эмпирик, «безразличны, неопределенны и неподсудны»

Мы не знаем, что они собой представляют, потому что видим не вещи, а лишь явления вещей

Вещи сами по себе, пишет Секст Эмпирик, «безразличны, неопределенны и неподсудны». Мы не знаем, что они собой представляют, потому что видим не вещи, а лишь явления вещей.

Воздерживаясь от суждений, скептик достигает желанной невозмутимости — а для греков это и есть главное условие счастья.

Греческий культ невозмутимости кажется прямой противоположностью современных представлений о счастье. Но на самом деле скептики пытаются сообщить нам одну важную вещь: жить можно как угодно, но к философии и науке это не имеет никакого отношения.

Античный скептик может жить, как все остальные люди: есть, когда захочется; спать, когда возникнет потребность; надевать клетчатые рубашки, если ему нравится именно этот узор. Ни одно из этих действий невозможно обосновать, основываясь лишь на разуме. Теоретически можно доказать, что движения не существует, как это сделал Зенон в знаменитом парадоксе об Ахиллесе и черепахе. Но люди, пишет Секст Эмпирик, «предпринимают путешествия пешком и морем, строят корабли и дома и рожают детей, не обращая внимания на рассуждения против движения и возникновения».

Теоретически мы можем сомневаться во всем. Но на практике сделать это невозможно.

Человек следует не за вещами, а за феноменами, отражениями вещей, утверждают скептики. Он руководствуется не знаниями, а соматическими маркерами, мог бы добавить Дамасио.

В своем крайнем виде скептицизм всегда приводит к иррационализму. Если ничего нельзя доказать, то все абсурдно. А если все абсурдно, в реальность можно только верить. Неудивительно, что аргументы скептиков охотно использовали Отцы Церкви в полемике против древней философии и языческих верований.

В XVI веке в Европе впервые опубликовали немногие сохранившиеся сочинения скептиков. С этого началась мода на пирронизм, которая могла приобретать самые разные формы. Автор знаменитых «Опытов» Мишель Монтень, признавая слабость человеческих познаний, вовсе не отвергает веру. Не делает этого и Рене Декарт, который строит основу научной философии, пользуясь методом радикального сомнения.

Орты

Прямоугольная система координат (любой размерности) также описывается набором ортов (единичных векторов), сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты составляют базис, притом ортонормированный.

В трёхмерном случае такие орты обычно обозначаются

i{\displaystyle \mathbf {i} }, j{\displaystyle \mathbf {j} } и k{\displaystyle \mathbf {k} }

или

ex{\displaystyle \mathbf {e} _{x}}, ey{\displaystyle \mathbf {e} _{y}} и ez{\displaystyle \mathbf {e} _{z}}.

Могут также применяться обозначения со стрелками (i→{\displaystyle {\vec {i}}}, j→{\displaystyle {\vec {j}}} и k→{\displaystyle {\vec {k}}} или e→x{\displaystyle {\vec {e}}_{x}}, e→y{\displaystyle {\vec {e}}_{y}} и e→z{\displaystyle {\vec {e}}_{z}}) или другие в соответствии с обычным способом обозначения векторов в той или иной литературе.

При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:

• i,j=k;{\displaystyle =\mathbf {k} ;}
• j,k=i;{\displaystyle =\mathbf {i} ;}
• k,i=j.{\displaystyle =\mathbf {j} .}

Для более высоких, чем 3, размерностей (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто это

e1,e2,e3,…en,{\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3},\dots \mathbf {e} _{n},}

где n — размерность пространства.

Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):

a=a1e1+a2e2+a3e3+⋯+anen{\displaystyle \mathbf {a} =a_{1}\mathbf {e} _{1}+a_{2}\mathbf {e} _{2}+a_{3}\mathbf {e} _{3}+\dots +a_{n}\mathbf {e} _{n}}

или

a=∑i=1naiei,{\displaystyle \mathbf {a} =\sum \limits _{i=1}^{n}a_{i}\mathbf {e} _{i},}

а для ортонормированного базиса координаты еще и очень легко найти через скалярные произведения с ортами:

ai=a⋅ei.{\displaystyle a_{i}=\mathbf {a} \cdot \mathbf {e} _{i}.}

Технические характеристики

приведены соответственно в таблице 2 и таблице 3.

Таблица 2 — Метрологические характеристики

Наименование характеристики	Значение характеристики
Диапазон измерений скорости движения ТС, км/ч — при измерении скорости в зоне контроля	от 1 до 300
— при измерении скорости на контролируемом участке дороги	от 1 до 300
Пределы допускаемой абсолютной погрешности измерений скорости ТС, км/ч: — в зоне контроля — в диапазоне от 1 до 100 км/ч включ.	±1
— в диапазоне св. 100 до 300 км/ч	±2
— на контролируемом участке дороги — в диапазоне от 1 до 100 км/ч включ.	±1
— в диапазоне св. 100 до 300 км/ч	±2
Минимальная протяженность контролируемого участка дороги, м	300
Пределы допускаемой абсолютной погрешности синхронизации времени относительно шкалы UTC (SU), мс	±1
Границы допускаемой абсолютной инструментальной погрешности (при доверительной вероятности 0,95) определения координат в плане, м	±3

Наименование характеристики	Значение характеристики
Время установления рабочего режима, мин, не более:
в летнее время	5
в зимнее время	40
Условия эксплуатации:
Для ИК:
— температура окружающей среды, °С	от -50 до +60
— относительная влажность при температуре 35 °С, %, не более	95
— атмосферное давление, кПа	от 60 до 106,7
Для ВС:
— температура окружающей среды, °С	от +10 до +35
— относительная влажность при температуре 35 °С, %, не более	80
— атмосферное давление, кПа	от 84 до 106,7
Степень защиты по ГОСТ 14254-96
— ИК	IP65
— ВС	IP44
Напряжение питания от сети переменного тока частотой (5 0± 1) Гц, В	от 187 до 268
Потребляемая мощность, В • А, не более
ИК	100
ВС	1000
Габаритные размеры составных частей комплексов (длинах
ширинахвысота), мм, не более:
— ИК:
распознающая камера	150x100x300
управляющий блок	400x300x300
инфракрасный осветитель	70x80x120
— ВС	500x200x500
Масса составных частей систем, кг, не более:
— ИК:
распознающая камера	5
управляющий блок	27
инфракрасный осветитель	2
— ВС	5

Максимы

На этом «Рассуждения о методе» Рене Декарта не заканчиваются. Философ использует аналогию с восстановлением дома на основе надежного фундамента и связывает ее с идеей необходимости временного проживания, когда его собственный дом перестраивается. Декарт принял следующие три максимы, чтобы эффективно функционировать в реальном мире, экспериментируя со своим методом радикальных сомнений. Они сформировали рудиментарную систему убеждений, из которой можно было действовать до того, как он разработал новую систему, основанную на истинах, которые он открыл с помощью своего метода.

Первая максима заключалась в том, чтобы подчиняться законам и обычаям своей страны, твердо придерживаясь веры, в которой, по милости Божьей, его воспитывали с детства и регулировали его поведение во всех других вопросах в соответствии с самыми умеренными требованиями. Декарт советует быть таким же решительным, каким был и он сам, особенно в своих сомнениях. Всегда старайтесь побеждать себя, а не удачу, и меняйте свои желания, а не порядок мира, и вообще приучите себя к убеждению, что кроме наших собственных мыслей нет ничего абсолютного в нашей власти. Так что когда мы сделаем все, что в наших силах, любой результат не может считаться неудачей.

Главные идеи и понятия

В первую очередь необходимо разобраться в основных взглядах учёного. Под рационализмом понимается мнение с позиции разума, а с философской точки зрения — это единое целое из всех направлений, ставящих во главу угла основные пункты анализа:

• Субъективно — мышление и рассудок.
• Объективно — логику и разумность.

Этот метод говорит, что человеческий ум наделён врождёнными идеями, или интуицией, которые определяют итоги познания. А ещё заслугой философа стало предложение двух принципов для всех исследователей:

• Внешний мир движется исключительно механистически.
• Внутренний — рассматривается только с позиции здравого рассудка и самосознания.

Двойственность материального и идеального

Декарт много работал над основным вопросом философии, и в своих суждениях демонстрировал дуализм – то есть, принятие сразу двух начал, материального и идеального. Но несмотря на это, ученый был материалистом в вопросах, касающихся объяснений природы. Вселенная устроена из материи и движения, в ней нет божественной силы. Так же он рассуждал и о животных, называя их сложными машинами.

Но, что касается человека, то здесь речь идет о нематериальной душе и участии Бога. В этой концепции и заключалось дуалистическое отношение ученого. Декарт полагал, что деятельность души человека невозможно объяснить, исходя из механических принципов. Мышление не отождествимо с телесными органами, оно представляет собой чистый дух. Пластичность и способность адаптации души доказывает ее божественное происхождение. Основным отличием человеческого мышления является универсальность, способность служить при различных обстоятельствах.

Не менее важным отличием человека от машины (в том числе, и от животных), Декарт считал наличие осмысленной речи. Он рассуждал, что даже слабоумные люди могут пользоваться осмысленной речью. Глухонемые изобретают осмысленный язык жестов. Животные же, даже если они здоровы и выращены в идеальных условиях, неспособны на подобное. У животных есть органы для произнесения слов, но нет мышления, как у людей.

Философия Декарта

Французский дворянин, вдохновившись работами своих современников, хотел разработать универсальный метод научного познания жизни.

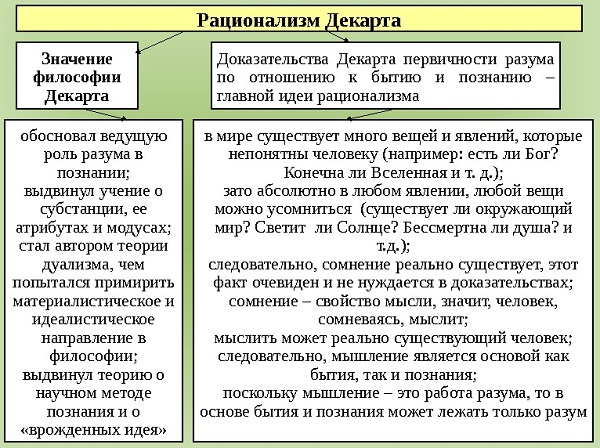
В своих трактатах он использовал антисхоластический метод, поскольку Декарт критиковал схоластику и шел рационалистическим путем по пути познания картины мира, в отличие от своего друга Бекона, который изучал природу эмпирическим методом.

Рене говорил, что открытия делаются не чувствами, а разумом. Именно он направляет опыт в нужное русло и делает процесс изучения реальности рациональным. Отсюда его теории рационализма.

Суть его философских трактатов, учения и теории познания в следующем:

1. Познание появляется от незнания и инертным образом достигает правды.
2. Разум должен быть основой дедуктивного знания для выведения всех необходимых следствий. Дедукция требуется, поскольку вывод не всегда понятен. Она является движением мысли от общего к частному и действием разума, с помощью которого делаются все заключения и неизвестное становится известным.

На основе своих суждений Декарту удалось вывести три правила:

• все вопросы обязаны содержать неизвестное звено;
• неизвестное звено обязано обладать характерными особенностями для правильного истолкования метода;
• каждый вопрос обязан содержать и некое известное.

По его мнению, сомнение — исходный путь рационалистического метода познания. Его философия была направлена не на уничтожение знаний, а на избавление человечества от идолов с предрассудками.

К тому же, мышление является исходной точкой интеллектуального мышления, и только оно позволяет выявить абсолютную и непосредственную достоверность знания. Только рационалистический метод поможет науке развиваться и превратить ее в важную сферу деятельности людей.

Несмотря на развернутость и ясность его философского течения, его методология имеет противоречия. Дело в том, что Декарт был гносеологом, но хотел уйти от гносеологии и перейти к онтологии. Мышление, по его мнению, открыто внешнему миру.

Также, несмотря на отрицание некоторых идей современников, он брал идеи платонизма как главный атрибут знаний и ввел учение о врожденной идее — божественной, числовой, фигурной идее.

Обозначения и соглашения

Декартовы координаты точки обычно записываются в круглых скобках и разделяются запятыми, как в (10, 5) или (3, 5, 7) . Происхождение часто называют с заглавной буквой O . В аналитической геометрии неизвестные или общие координаты часто обозначаются буквами ( x , y ) на плоскости и ( x , y , z ) в трехмерном пространстве. Этот обычай исходит из соглашения об алгебре, которое использует буквы в конце алфавита для неизвестных значений (таких как координаты точек во многих геометрических задачах) и буквы в начале для заданных величин.

Эти обычные имена часто используются в других областях, таких как физика и инженерия, хотя могут использоваться и другие буквы. Например, на графике, показывающем, как давление изменяется со временем , координаты графика могут быть обозначены p и t . Каждая ось обычно называется в честь координаты, которая измеряется вдоль нее; так что один говорит ось х , то ось у , то т-оси и т.д.

Другое распространенное соглашение для именования координат — использовать индексы, как ( x ₁ , x ₂ , …, x _n ) для n координат в n -мерном пространстве, особенно когда n больше 3 или не указано. Некоторые авторы предпочитают нумерацию ( x , x ₁ , …, x _{n −1} ). Эти обозначения особенно полезны в компьютерном программировании : сохраняя координаты точки в виде массива , вместо записи , нижний индекс может служить для индексации координат.

В математических иллюстрациях двумерных декартовых систем первая координата (традиционно называемая абсциссой ) измеряется по горизонтальной оси, ориентированной слева направо. Вторая координата ( ордината ) затем измеряется по вертикальной оси, обычно ориентированной снизу вверх. Маленькие дети, изучающие декартову систему, обычно изучают порядок чтения значений перед закреплением концепций осей x -, y — и z , начиная с двумерной мнемоники (например, «Пройдите по коридору, затем поднимайтесь по лестнице», похожую на прямую поперек оси x, затем вверх вертикально вдоль оси y ).

Однако компьютерная графика и обработка изображений часто используют систему координат с осью Y, ориентированной вниз на экране компьютера. Это соглашение было разработано в 1960-х (или ранее) из того способа, которым изображения изначально хранились в буферах дисплея .

Для трехмерных систем принято изображать плоскость xy горизонтально с добавлением оси z для обозначения высоты (положительное значение вверх). Кроме того, существует соглашение об ориентации оси x по направлению к наблюдателю, смещенной вправо или влево. Если диаграмма ( трехмерная проекция или двухмерный перспективный чертеж ) показывает оси x и y по горизонтали и вертикали, соответственно, тогда ось z должна быть показана направленной «за пределы страницы» к зрителю или камере. На такой двухмерной диаграмме трехмерной системы координат ось z будет выглядеть как линия или луч, указывающий вниз и влево или вниз и вправо, в зависимости от предполагаемого зрителя или перспективы камеры . На любой диаграмме или отображении ориентация трех осей в целом произвольна. Однако ориентация осей относительно друг друга всегда должна соответствовать правилу правой руки , если специально не указано иное. Все законы физики и математики предполагают эту , что обеспечивает последовательность.

Для трехмерных диаграмм имена «абсцисса» и «ордината» редко используются для x и y соответственно. Когда они есть, координату z иногда называют аппликатой . Слова абсцисса , ордината и аппликата иногда используются для обозначения осей координат, а не значений координат.

Квадранты и октанты

Четыре квадранта декартовой системы координат

Оси двумерной декартовой системы делят плоскость на четыре бесконечные области, называемые квадрантами , каждая из которых ограничена двумя полуосями. Они часто нумеруются с 1-го по 4-й и обозначаются римскими цифрами : I (где знаки двух координат — I (+, +), II (-, +), III (-, -) и IV (+, -). Когда оси строятся по математическому обычаю, нумерация идет против часовой стрелки, начиная с правого верхнего («северо-восточного») квадранта.

Точно так же трехмерная декартова система определяет разделение пространства на восемь областей или октантов в соответствии со знаками координат точек. Условие, используемое для наименования конкретного октанта, состоит в перечислении его знаков, например (+ + +) или (- + -) . Обобщение квадранта и октанта до произвольного числа измерений — это ортант , и применяется аналогичная система именования.

Философия

Философскому учению Рене Декарта был свойственен дуализм: он полагал, что существует и идеальная субстанция, и материальная. И то, и другое начала признавались им самостоятельными. Концепция Рене Декарта также предполагает признание наличия в нашем мире двух видов сущностей: мыслящей и протяженной. Ученый полагал, что источником обеих сущностей является Бог. Он формирует их по одинаковым законам, творит материю параллельно с ее покоем и движением, а также сохраняет субстанции.

Философский трактат Рене Декарта

Своеобразный универсальный метод познания Рене Декарт видел в рационализме. При этом само познание ученый считал предпосылкой к тому, что человек будет господствовать над силами природы. Возможности разума по Декарту скованы несовершенством человека, его отличиями от совершенного Бога. Рассуждение Рене о познании в таком ключе, по сути, заложило базу рационализма.

Рене Декарт в молодости

Исходным пунктом большинства поисков Рене Декарта в области философии было сомнение в правдивости, безошибочности знаний, относящихся к общепризнанным. Цитата Декарта «Я мыслю – следовательно, я существую» обусловлена этими рассуждениями. Философ заявлял, что каждый человек может сомневаться в существовании своего тела и даже внешнего мира в целом. Но при этом однозначно существующим останется это сомнение.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Краткая биография

Рене Декарт (Rene Descartes) (годы жизни 1596 — 1650) — знаменитый француз Нового времени, изучавший разделы математики, философии, физики, физиологии, метафизики, человек, который изучал аналитический вид геометрии, алгебраический вид символики и новоевропейский рационализм.

Его биография, как и всех современников, интересна. Он родился на свет в конце марта 1596 года в небольшом французском городке Лаэ на востоке Турень. Жил в семье советника и причислялся к членам древнего, но разорившегося рода дворян де Карт, который позднее дал название новому течению в философии — картезианскому сомнению или картезий.

По жизни он был классический представитель дворянства. С малых лет обучался в иезуитской коллегии Ла Флеш. Здесь его обучали не естественным наукам, а религии. Именно поэтому Декарт пародоксально потерял интерес к схоластическому течению философии.

В коллегии он завел дружбу с будущим математиком Мерсенном, и они вместе стали участниками научного сообщества. Окончив коллегию, Рене стал студентом Пуатьейского университета и в 1616 году получил бакалавриат по праву. В 1617 году он встал в ряды армии и исследовал Европу.

В 1618 году философ познакомился с человеком, который смог повлиять на его взгляды. Этим человеком стал Исаак Бекман, считавшийся физиком и натурфилософом. Именно он повлиял на молодого человека и тот стал углубляться в математический вид рассуждений и универсальных методов познания.

В 1628 году иезуиты узнали о вольнолюбии Декарта, и он был осужден за ересь. Именно тогда преследуемый ученый покидает французскую землю и переезжает в голландский городок. Однако и здесь он не нашел свой дом и стал часто переезжать.

В 1634 году Рене написал первый трактат «Мир», но не стал его публиковать, боясь расправы от церкви. В 1637 году ученый опубликовал «Рассуждение о методе», которую позднее назвали трудом философской мысли Новой Европы.

Основной его труд был издан в 1641 году — «Размышления о первой философии», а спустя 3 года вышла работа «Первоначала философии». Последняя работа была издана за год до смерти — в 1649 году. «Страсти души» сильно смогли повлиять на мысль Европы.

Кроме философских трактатов, Рене занимался математикой и издавал по ней свои труды. В 1637 году он издал труд по геометрии и ввел новый метод изучения координат.

В 1650 году ученый переезжает в Стокгольм по приглашению шведской королевы. Из-за жесткого графика работы в королевстве и холодного климата, он умер от пневмонии. Есть версия, что Рене погиб из-за отравления мышьяком, чтобы королева не стала еретичкой.

После смерти его работы долго не публиковались. Более того, их запрещали читать и изучать. Только спустя столетие люди познакомились с его публикациями. В 1667 году тело ученого отвезли на родину и захоронили там.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат OX{\displaystyle OX}, OY{\displaystyle OY} и OZ{\displaystyle OZ}. Оси координат пересекаются в точке O{\displaystyle O}, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно (не обязательно) одинаковы для всех осей. OX{\displaystyle OX} — ось абсцисс, OY{\displaystyle OY} — ось ординат, OZ{\displaystyle OZ} — ось аппликат.

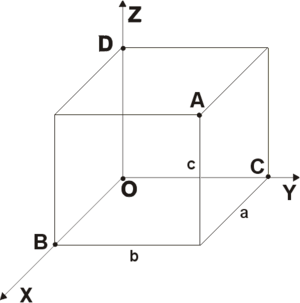
Рис. 2

Положение точки A{\displaystyle A} в пространстве определяется тремя координатами x{\displaystyle x}, y{\displaystyle y} и z{\displaystyle z}. Координата x{\displaystyle x} равна длине отрезка OB{\displaystyle OB}, координата y{\displaystyle y} — длине отрезка OC{\displaystyle OC}, координата z{\displaystyle z} — длине отрезка OD{\displaystyle OD} в выбранных единицах измерения. Отрезки OB{\displaystyle OB}, OC{\displaystyle OC} и OD{\displaystyle OD} определяются плоскостями, проведёнными из точки A{\displaystyle A} параллельно плоскостям YOZ{\displaystyle YOZ}, XOZ{\displaystyle XOZ} и XOY{\displaystyle XOY} соответственно.

Координата x{\displaystyle x} называется абсциссой точки A{\displaystyle A},

координата y{\displaystyle y} — ординатой точки A{\displaystyle A},

координата z{\displaystyle z} — аппликатой точки A{\displaystyle A}.

Символически это записывают так:

A(x,y,z){\displaystyle A(x,\;y,\;z)}

или

A=(x,y,z){\displaystyle A=(x,\;y,\;z)}

или привязывают запись координат к конкретной точке с помощью индекса:

xA,yA,zA{\displaystyle x_{A},\;y_{A},\;z_{A}}

и т. п.

Каждая ось рассматривается как числовая прямая, т. е. имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка B{\displaystyle B} лежала не как на рисунке — на луче OX{\displaystyle OX}, а на его продолжении в обратную сторону от точки O{\displaystyle O} (на отрицательной части оси OX{\displaystyle OX}), то абсцисса x{\displaystyle x} точки A{\displaystyle A} была бы отрицательной (минус расстоянию OB{\displaystyle OB}). Аналогично и для двух других осей.

Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси OX{\displaystyle OX} против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY{\displaystyle OY}, если этот поворот наблюдать со стороны положительного направления оси OZ{\displaystyle OZ}).

Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.

Формулировка Править

В первых главах Декарт постоянно упоминает то Бога, то «злого гения», обманывающего его, из-за чего нижеприведённый отрывок не всем является первоисточником. Однако автор статьи данной решил привести именно его, так как именно он ведёт к идеи «Cogito ergo sum» и при том несёт в себе большую часть написанных ранее Декартом шагов размышления:

«Итак, я допускаю, что все видимое мною ложно; я предполагаю никогда не существовавшим все, что являет мне обманчивая память; я полностью лишен чувств; мои тело, очертания (figura), протяженность, движения и место – химеры. Но что же тогда остается истинным? Быть может, одно лишь то, что не существует ничего достоверного.

Однако откуда мне известно, будто, помимо перечисленных, не существует других вещей, относительно которых не может быть ни малейшего сомнения? Ведь, возможно, есть некий Бог – или как бы мы это ни именовали, – внушивший мне эти самые мысли? И прав ли я в данном случае – ведь я и сам могу быть их виновником? Так не являюсь ли, по крайней мере, и я чем-то сущим? Но ведь только что я отверг в себе всякие чувства и всякое тело. Тем не менее я колеблюсь; что же из этого следует? Так ли я тесно сопряжен с телом и чувствами, что без них немыслимо мое бытие? Но ведь я убедил себя в том, что на свете ничего нет – ни неба, ни земли, ни мыслей, ни тел; итак, меня самого также не существует? Однако, коль скоро я себя в чем-то убедил, значит, я все же существовал? Но существует также некий неведомый мне обманщик, чрезвычайно могущественный и хитрый, который всегда намеренно вводит меня в заблуждение. А раз он меня обманывает, значит, я существую; ну и пусть обманывает меня, сколько сумеет, он все равно никогда не отнимет у меня бытие, пока я буду считать, что я – нечто. Таким образом, после более чем тщательного взвешивания всех «за» и «против» я должен в конце концов выдвинуть следующую посылку: всякий раз, как я произношу слова Я есть, я существую или воспринимаю это изречение умом, оно по необходимости будет истинным»