Эвристический метод обучения
Содержание:
- Практические советы
- Что такое методы исследования?
- Угостите напитком
- Уточнение корней
- Метод Гаусса-Зейделя
- Методы эффективного принятия групповых управленческих решений
- Метод половинного деления (метод дихотомии)
- Матрица Кано
- Выделите время на обдумывание
- Её друг/подружка случайно оказалась рядом с тобой на танцполе
- Способы принятия управленческих решений
- Определение причин проблем с помощью ответов на вопрос “почему”
- Метод Ньютона (метод касательных)
- Особенности алгоритма метода искусственного базиса
Практические советы
Независимо от возраста и социального статуса, люди попадают в трудные ситуации, выход из которых связан с принятием решения. Веками совершенствовались правила и стратегии формирования выбора и знакомство с ними наверняка не станет откровением, но, возможно, будет полезным в экстренных обстоятельствах.
Комплекс рекомендаций для правильного решения:
Владение информацией расширяет возможности выбора. Необходимы факты, четкие данные без эмоций и приукрашивания.
В потоке сведений присутствует много лишнего, такие элементы отсеивают. Все, что не подтверждено надежным источником, откидывают в сторону, оставляя суть.
Концентрация внимания в точке затруднений помогает найти выход
Важно сохранять спокойствие.
Использование опыта и знаний предыдущих поколений не стоит игнорировать. Иногда, прислушиваясь к тому, что говорят близкие, можно получить готовое решение и применить его к ситуации.
Изменение обстоятельств сбивает с толку
В таких случаях проявляют гибкость, варьируя возможности решения проблемы.
Трезвая оценка сложившейся обстановки помогает быстрее разрешить ее. Нельзя допускать эмоций, даже когда дело касается личности.
Приняв решение, необходимо сохранять последовательность и действовать так, как было задумано. Четко сформированная стратегия поддерживает порядок и баланс в мыслях и чувствах.
Психологи дают советы способные упростить выбор и помогающие разобраться в себе. Но главным аспектом легкого принятия решения является отсутствие страха. Не нужно бояться делать ошибки. Даже правильные действия иногда приводят к неожиданным и не всегда приятным последствиям.
Что такое методы исследования?
Это первый вопрос, в котором следует разобраться. Итак, методы исследования – это те шаги, которые мы выполняем на пути к цели своей работы. Это способы, которые помогают нам решить поставленные задачи.
По причине их огромного количества существуют разные классификации методов исследования, подразделения на виды, объединения в группы. Прежде всего, их принято разделять на две категории: универсальные и частные. Первая категория применима для всех отраслей знания, а вторая отличается более узкой направленностью и охватывает те методы, которые применяются строго в той или иной сфере науки.
Следующую классификацию рассмотрим более подробно и выделим их виды: эмпирические, теоретические, количественные и качественные. Далее рассмотрим методы, применимые в конкретных сферах познания: педагогике, психологии, социологии и прочих.
Угостите напитком

Отличный повод начать знакомство — предложить девушке угостить ее напитком. Но есть большой риск, что она просто использует этот шанс, ради бесплатного алкоголя, но не общения с парнем, и когда выпивка закончится или надоест, то она найдет повод уйти. Поэтому тратить деньги на неизвестную девушку не разумно, потому как вложения могут оказаться напрасными.
Уточнение корней
Для уточнения корней может использоваться один из следующих методов:
Метод Гаусса-Зейделя
Сущность этого метода состоит в том, что в нём переносятся в правые части все члены уравнений, индекс при которых больше индекса, выражаемого $x$.
В краткой форме это можно записать так:
$(L + D) \cdot \overrightarrow{x} = -U\overrightarrow{x} + \overrightarrow{b}$
Сами итерации в методе Гаусса-Зейделя производятся по формуле:
$(L +D)\overrightarrow{x}^{(k+1)}=-U\overrightarrow{x}^{(k)} + \overrightarrow{b}$
Метод Гаусса-Зейделя похож на метод Якоби, но здесь полученные значения переменных используются не исключительно для следующей итерации, а сразу для следующего вычисления значения $x$.
Пример 1
Метод простых итераций: пример решения
Дана система уравнений:
$\begin{cases} 10x_1 – x_2 + 2x_3 = 6 \\ -x_1 + 11x_2 – x_3 + 3x_4 = 25 \\ 2x_1- x_2 + 10x_3 -x_4 = -11 \\ 3x_2 – x_3 + 8x_4 = 15 \end{cases}$
Решите данную систему с помощью метода простых итераций.
Выберем в качестве нулевого приближения корни $(0; 0; 0; 0)$ и подставим их в преобразованную систему:
$\begin{cases} x_1 = (6 + 0 – (2 \cdot 0))/10 = 0,6 \\ x_2 = (25 + 0 – 0 – (3 \cdot 0))/11 = 25/11 = 2,2727 // x_3 = (-11 – (2 \cdot 0) + 0 + 0) /10 = -1,1 \\ x_4 = (15 – (3 \cdot 0) + 0) / 8 = 1,875\\ \end{cases}$
Проведём 5 итераций, используя на каждой результат, полученный с предыдущей и для них получим следующую таблицу:
Рисунок 1. Таблица итераций для решения СЛАУ. Автор24 — интернет-биржа студенческих работ
Продолжать вычисление можно до достижения заданной требуемой точности. Точный ответ системы — $(1; 2; -1; 1)$.
Методы эффективного принятия групповых управленческих решений
Как мы уже писали, принятие решений в группах имеет свои преимущества и недостатки. Чтобы данный процесс проходил максимально гладко, вы можете использовать один из методов, описанных в этой главе. Мы определили семь методов группового принятия решений, поэтому есть большая вероятность, что один из этих вариантов будет правильным для ваших нужд.
Модель принятия решений Хоя-Тартера. Изначально созданная для использования в школьной системе, модель принятия решений Хоя-Тартера может фактически применяться в ряде различных условий. Если вы владелец или руководитель какой-либо организации, вы уже знаете, насколько сложно принимать решения. В частности, может быть трудно решить, как принимать эти решения, с точки зрения того, кого вы должны привлечь, что вы должны учитывать в процессе и многое другое.
В данной модели основная цель состоит в том, чтобы точно определить, кто должен быть включен в процесс принятия управленческих решений. Разные решения требуют разного вклада от разных людей, поэтому определить, кого следует включить в принятие решения, а кого не учитывать, является ключевым шагом, который нельзя игнорировать. Включение не тех людей или отсутствие правильных людей – ошибка, которая может иметь серьезные последствия.
Данная модель требует от вас создание матрицы, которая будет заполнена оценками опыта и того, будет ли человек лично заинтересован в решении. Чтобы понять, как именно работает эта модель, может потребоваться некоторое время, но это стоит усилий из-за ее эффективности.
Метод множественного голосования. Если вы хотите использовать голосование, чтобы время от времени принимать важные управленческие решения, вы можете использовать популярный метод принятия решений с несколькими голосами. С помощью этого метода вы можете выбрать наиболее популярные варианты из списка, чтобы получить представление о консенсусе группы. Множественное голосование – это не всегда правильное заключение, но оно может быть идеальным в определенных обстоятельствах.
Если вы хотите использовать метод множественного голосования, первое, что вам нужно сделать – это составить список идей, которые станут предметом вашего голосования. Попросите команду, которая работает над этим проектом, сотрудничать в создании списка. Сначала вы можете поместить любую идею в список, но вам необходимо немного сузить и «очистить» его, прежде чем он пойдет на голосование.
Перед тем как принять участие в голосовании, вы должны решить, сколько именно голосов может отдать каждый участник. Обычно каждому человеку разрешается голосовать примерно за 1/3 идей из списка. Таким образом, при наличии списка из 15 пунктов каждому человеку будет разрешено отдать пять голосов.
После того как все голоса поданы и собраны, все, что вам нужно сделать, это подсчитать итоги и определить идеи-победители. Если хотите, вы можете сузить список идей-претендентов и провести повторное голосование, дополнительно сконцентрировав свой список лишь на нескольких самых сильных вариантах. Множественное голосование – это идеальный способ оценить мнение большой группы, когда имеются несколько идей.
Модифицированный метод Борда. Данный метод является так называемым расширением множественного голосования. Он работает аналогичным образом, взвешиваются только голоса, чтобы потенциально достичь более значимого результата. Вместо того чтобы голосовать только за один элемент или голосовать за несколько пунктов, как в случае системы с множественным голосованием, вы будете предлагать каждому избирателю присваивать очки выбранным им идеям.
Перед началом голосования вам нужно будет проинформировать каждого человека о том, сколько идей они могут поддержать в своем бюллетене. Например, при голосовании 10-ти пунктов каждый избиратель может поддержать 5 из 10 идей.
Таким образом, каждый человек сможет выбрать 5 из 10 идей. Выбирая эти пять, они обязаны дать каждой из них значение балла от 1 до 5. Лучшая для них концепция из списка получит 5 баллов, хорошее предложение получит 4 балла и так далее до пятой выбранной идеи. Пять предложений, за которые они решили не голосовать, не получат баллов.
Чтобы выбрать лучшее управленческое решение в модифицированном методе Борда – просто подсчитайте баллы голосования. Лучше используйте электронную таблицу для этой задачи, поскольку вы легко сможете изменить порядок электронных таблиц, чтобы отфильтровать идеи с наивысшими балами.
Метод половинного деления (метод дихотомии)
Если x, x1 — приближенные значения корня уравнения f(x) = 0 и выполняется условие
то последующие приближения находятся по формуле
и вычисляется f(xi). Если f(xi)=0, то корень найден. В противном случае из отрезков выбирается тот, на концах которого f(x) принимает значения разных знаков, и проделывается аналогичная операция. Процесс продолжается до получения требуемой точности.
Геометрическая интерпретация метода дихотомии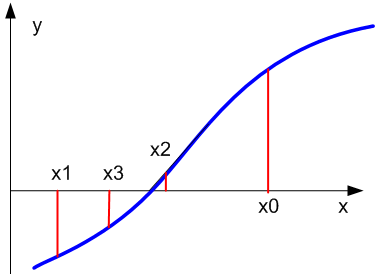 Реализация на C++
Реализация на C++
12345678910111213141516171819202122232425262728
#define _USE_MATH_DEFINES#include <iostream>#include <cmath>using namespace std;double func(double x){ return (sin(M_PI*x / 180) — 1 / x);}double find(double x0, double x1, double eps){ double left = x0, right = x1, x, fl, fr, f; int iter = 0; cout << «x0= » << x0 << » x1= » << x1 << » «; do { x = (left + right) / 2; f = func(x); if (f > 0) right = x; else left = x; iter++; } while (fabs(f) > eps && iter<20000); cout << iter << » iterations» << endl; return x;}int main() { cout << find(1.0, 10.0, 0.000001); cin.get(); return 0;}
 генетические алгоритмыАлгоритмизация
генетические алгоритмыАлгоритмизация
Матрица Кано
Автор — японский бизнес-консультант Нариаки Кано. Метод разработан в 1984 году. Отлично подходит для приоритизации внедряемых в продукт функций или оптимизации уже реализованных. Может быть реализован в рамках работы по созданию и улучшению операционных процедур.
В основе подхода — оценка удовлетворенности пользователей продукта.
Матрица приоритизации по Кано представляет собой систему координат, где по вертикальной оси —
шкала удовлетворенности продуктом
, а по горизонтальной — функциональность.
Приоритизируемые решения модель разделяет на несколько групп:
-
Must Be (M), или обязательные компоненты продукта — функции, без которых ваш продукт или процесс невозможен. Например, для системы документооборота это возможность быстрого обмена электронными документами. Для автомобиля — руль, тормозная система, колеса, мотор и т.д.
-
Indifferent (I), или функции безразличия — это те функции, которые для части пользователей важны, для части — нет, но большинство относится к ним равнодушно. В случае с системой документооборота это может быть наличие шаблонов для создания документов. А для автомобиля — наличие дополнительного зеркальца для мейкапа со стороны водителя.
-
Performance (P), или функции одномерности — это те функции, которые при отличной их реализации вызовут у пользователя положительные эмоции и наоборот. Для системы документооборота это может быть автозаполнение реквизитов контрагентов-физлиц по сканированной копии страниц паспорта. Если реализуете функцию хорошо — будет великолепно, но если автозаполнение будет приводить к ошибкам, то это катастрофа. Для автомобиля к таким функциям можно отнести электрический двигатель. Если это будет стабильная и длительная работа, то вы создали инновационный и любимый многими продукт. Если же речь идет о нестабильной и кратковременной работе, то есть риск потерять даже самых лояльных пользователей.
-
Attractive (A), или функции, вызывающие восторг, — дополнительные «плюшки», которые повысят удовлетворенность пользователя, но их отсутствие, скорее всего, не сильно повлияет на решение пользоваться продуктом. В автомобиле это может быть стеклянный потолочный люк, а в системе документооборота — кастомизация интерфейса программного обеспечения по цветам и дизайну.
Понять, как именно пользователь относится к процессу или продукту, можно путем опроса. Анкета состоит из двух вопросов:
-
Как бы вы себя чувствовали, если бы продукт имел данную функцию?
-
Как бы вы себя чувствовали, если бы продукт не имел данную функцию?
Среди вариантов ответа:
На следующем этапе вы подсчитываете число ответов в той или иной категории, определяя по максимальному числу балов приоритетные функции. Категории ответов M, P, I — плюс один балл за каждый ответ. Категории I, R, Q — минус один балл за ответ.
В нашем примере с автомобилем высокий уровень безопасности — сомнительный тип ответа. А вот наличие GPS — приятный, но не критичный бонус.
При равных баллах в первую очередь следует реализовать задачи уровней Must be, затем — Attractive и Performance. От Indifferent и Reverse стоит отказаться совсем. Высокая доля ответов Questionable — повод провести анкетирование заново.
Для того чтобы упростить процесс приоритизации, можно попросить пользователей каждой анализируемой функции присвоить степень важности от 1 до 10. Рассчитав среднее значение для каждой функции, вы получаете дополнительный аргумент в ее пользу или наоборот
Данный показатель также можно ввести в таблицу.
Выделите время на обдумывание
Разумеется, у вас нет времени. Но если на вас давит нехватка времени, то это сигнал о том, что вам следует в целом пересмотреть планирование повседневных задач. Парадоксально, но для быстрого принятия решений вам необходимо выделять на это время. Принятие решений — это задача, которой нужно гораздо больше внимания, чем вы обычно можете уделить, когда просыпаетесь посреди ночи с тревожной мыслью о срочной проблеме, которую вы до сих пор не решили.
Для обдумывания небольших решений вам, возможно, понадобится выделить всего 30 минут или час. Для более серьезных — несколько часов в течение двух или трех недель
Сколько бы времени вы ни отвели на принятие решения, важно обязательно отметить его в календаре и регулярно придерживаться выбранного расписания
Её друг/подружка случайно оказалась рядом с тобой на танцполе

Или не случайно? Может быть, он специально подошел к тебе, чтобы иметь возможность как бы невзначай пригласить и её поближе к тебе? Подумай.
Способы принятия управленческих решений
Принятие управленческих решений – это один из важнейших этапов управленческой деятельности. Невозможно говорить об успешной деятельности компании без знания грамотных подходов к приятию управленческих решений, ведь малейшая неопределенность в них может привести к трагичным последствиям.
Подходы к принятию стратегических решений
Человек, принимающий решения, использует свои знания, интуицию, суждения, рациональность, решение отражает мировоззрение личности. Поэтому принятие управленческих решений рассматривают как психологический процесс. Выделяют следующие подходы к принятию решений.
- Интуитивный. В этом случае решение принимается на основании ощущений личности, без проведения анализа плюсов и минусов. Обычно, такой подход свойственен людям, уже имеющим немалый управленческий опыт, их интуиция редко подводит. Хотя дело тут скорее не в ней, а в типовом поведении окружения, управленец просто знает чего от него можно ожидать. Но статистика показывает, что слепо полагаться на интуицию (знания) не стоит, иначе можно серьезно ошибиться с выбором стратегии, поэтому интуитивный подход рекомендуется сочетать с другими способами принятия решений.
- Основывающийся на суждениях. Этот выбор обуславливается накопленным опытом и знаниями человека. Логика в таком решении просматривается, а плюсами такого подхода является дешевизна и быстрота оценки ситуации. Но стоит помнить, что не все ситуации повторяются из раза в раз, и в совершенно новых условиях такой подход не сработает – руководитель не знает, что делать дальше, потому что ранее с подобным не сталкивался.
- Рациональный. Эта технология разработки решений не зависит от интуиции руководителя и его опыта, здесь главенствует строгий расчет. Для реализации рационального подхода, решение должно пройти следующие стадии:
- диагностика проблемы;
- формулировка критериев и ограничений для принятия решения;
- выявления альтернативных решений;
- оценка альтернатив;
- окончательный выбор решения.
Коллегиальный и индивидуальный способы принятия решений
Разделяют два способа принятия решения – коллегиальный и индивидуальный. Последний способ оправдан в тех случаях, когда перед управленцем стоят довольно простые задачи или риск сравнительно невелик. Но с усложнением задач управления (укрупнением производства) такой способ принятия решений становится неэффективным из-за своей субъективности.
Поэтому на крупных предприятиях чаще всего используется коллегиальный способ принятия решений. Он отличается большей объективностью и позволяет учесть все факторы, влияющие на фирму. Но у коллективного принятия решений есть существенный недостаток – низкий уровень оперативности. Этот способ можно подразделить на четыре подвида.
- Принятие решений методом простого большинства. Это всем нам известное голосование, правила предельно просты – как считает большинство, так и поступит руководитель. Недостатком является то, что мнение меньшинства не учитывается и это может быть опасно – гениальные идеи обычно генерирует малое число лиц. Кроме того, этот метод не позволяет учитывать мотивацию членов группы (почему они голосуют за это решение), а потому и уровень рациональности здесь будет довольно низок.
- Стратегия суммирования рангов. Решение будет соответствовать альтернативе, набравшей меньшую сумму рангов.
- Стратегия минимизации отклонений. Ее суть заключается в том, чтобы сделать различия между мнениями большинства и меньшинства минимальными.
Определение причин проблем с помощью ответов на вопрос “почему”
На базе вышеупомянутого вопроса существует множество успешных методик по анализу трудностей и их незамедлительному решению. К ним можно отнести:
- Небезызвестную в широких кругах технику “Пять почему” (которая использовалась в производстве известной компании Toyota);
- “Метод Сократа” (методика в формате диалога между двумя вымышленными индивидуумами);
- “Диаграмму Исикавы” (причинно-следственная диаграмма), а также массу остальных подобных методик.
Различия между ними, безусловно, имеются, но суть остается единой – это выявление причинно-следственных связей, которые могут скрываться в той или иной человеческой проблеме. И фигурирует везде один главный вопрос – “почему”.
Поиск решения проблемы со штрафами в рамках рассматриваемого метода нескольких “почему” будет выглядеть следующим образом:
1. Берем листок бумаги, карандаш или ручку и записываем следующее предложение: “Сегодня я был оштрафован, когда ехал на работу”.
2. Далее задаем сами себе вопрос: “Почему?”.
3. Ниже записываем на него ответ. К примеру: “Я слишком поздно проснулся”.
4. Снова спрашиваем себя: “Почему?”.
5. Находим ответ: “Потому что не сработал будильник”.
6. И вновь: “Почему?”.
7. “Потому что я забыл поменять в часах севшие батарейки на новые”.
Таким образом, вы спокойно находите причину проблем и приходите к искомому ранее результату: оказывается, что всему виной старые батарейки, которые дано уже следовало заменить. Стало ясно, что решить проблему регулярных опозданий, а также штрафов, можно всего лишь простой и доступной заменой батареек в будильнике. Конечно же, это всего лишь упрощенный пример, но в нем кроется алгоритм, способный качественно изменить вашу жизнь к лучшему, внеся в нее щепотку целительного анализа происходящих событий.
Суть вопроса “Почему”
Причины возникновения проблем разнообразны, как и сами проблемы. Пресловутые “почему”, конечно же, помогают найти “проблемные причины”, но таковой метод ответов на вопросы – это лишь крохотная крупица чего-то более глобального. Суть решения любых неурядиц кроется в самом подходе к процессу решения – в выстраивании правильной причинно-следственной связи.
Именно с ее помощью можно взять всего один небольшой негативный симптом, который у вас имеется (к примеру – подавленное настроение каждым вечером буднего дня), и выстроить цепочку, ведущую к глобальной причине. Многократно отвечая на вопрос “почему?” вы можете проследить связь между плохим подавленным настроением и, скажем, неурядицами на работе. Далее – между рабочими неурядицами и регулярным недосыпом. Далее – между недосыпом и, к примеру, долгим просиживанием по вечерам у компьютера. Так можно докопаться до истины и устранить зерно любого беспокойства, “выкорчевав” тем самым множество смежных проблем. А записывая или зарисовывая ход своих мыслей на бумаге, вы сможете все наглядно увидеть и проанализировать.
Владея методикой выстраивания логических цепочек и правильных ответов на конкретный вопрос “почему”, можно избавиться от ряда проблема и сделать свою жизнь понятной, построенной по прозрачным и ясным схемам. Берите на вооружение и меняйтесь.
Метод Ньютона (метод касательных)
Если известно начальное приближение x корня уравнения f(x)=0, то последовательные приближения находят по формуле
Графическая интерпретация метода касательных имеет вид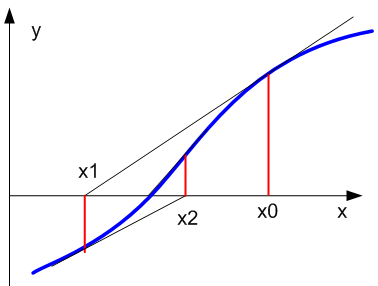 Реализация на C++
Реализация на C++
Для заданного уравнения
производная будет иметь вид
12345678910111213141516171819202122
#define _USE_MATH_DEFINES#include <iostream>#include <cmath>using namespace std;double find(double x, double eps){ double f, df; int iter = 0; cout << «x0= » << x << » «; do { f = sin(M_PI*x / 180) — 1 / x; df = M_PI / 180 * cos(M_PI*x / 180) + 1 / (x*x); x = x — f / df; iter++; } while (fabs(f) > eps && iter<20000); cout << iter << » iterations» << endl; return x;}int main() { cout << find(1, 0.00001); cin.get(); return 0;}
Результат выполнения
Особенности алгоритма метода искусственного базиса
- Виду того, что начальное опорное решение расширенной ЗЛП содержит искусственные переменные, входящие в целевую функцию с коэффициентами -М (max) или +М (min), оценка разложений векторов условий Δj= CбXj -cj состоит из двух слагаемых Δj= Δ’j +Δ’’j( M). Т.к. М – велико, то на первом этапе расчета для нахождения векторов, вводимых в базис, используется только слагаемое Δ’’j( M).
- Векторы, соответствующие искусственным переменным, которые выводятся из базиса опорного решения, исключаются из рассмотрения.
- После того как все векторы, соответствующие искусственным переменным, исключены из базиса, расчет продолжается обычным симплексным методом с использованием оценок Δ’j, не зависящих от М.
- Переход от решения расширенной ЗЛП к решению исходной ЗЛП осуществляется с помощью указанных ранее замечаний.
Пример. Найти решение следующей задачи.
Z(X)=x1+x2+4x3→max
xj≥0 (j=1,2,3)
Приведем задачу к каноническому виду
xj ≥ 0 (j=1,2,3,4,5,6)
Z(X)=x1+x2+4x3+0x4+0x5+0x6-Mx7→max
В первых двух уравнениях содержатся базисные переменные x4 и x5 (это дополнительные переменные), а в третьем базисная переменная отсутствует, поэтому введем искусственную переменную x7, которая и будет являться базисной. Решаем М-задачу.
Составим симплексную таблицу:
| Базис | Cб | В | 1 | 1 | 4 | -M | |||
| A1 | A2 | A3 | A4 | A5 | A6 | A7 | |||
| A4
A5← A7 |
-M |
20
24 6 |
1
2 1 |
4
1 1 |
1
3 |
1 |
0
1 |
-1 |
1 |
|
Z= 0-6М |
-1 |
-1
-1 |
-4 |
0
1 |
|||||
| A4←A5
A1 |
1 |
14
12 6 |
1 |
3
-1 1 |
1
3 |
1 |
0
1 |
1
2 1 |
|
| Z1=6 | -4↑ | -1 | |||||||
|
←A4
A3 A1 |
0
4 1 |
10
4 6 |
1 |
10/3
1/3 1 |
0
1 |
1 |
-1/3
1/3 |
1/3
2/3 -1 |
|
| Z2=22 | -4/3 | 4/3 | 5/3 | ||||||
| A2
A3 A1 |
1
4 1 |
3
5 3 |
1 |
1 |
0
1 |
2/10 | 1/10 | 1/10 | |
| Z3=26 | 4/10 | 6/5 | 9/5 |
3max
Для более подробного ознакомления с алгоритмом M-метода рекомендуем воспользоваться калькулятором.
Примербольшой положительный штраф М
Решим прямую задачу линейного программирования симплексным М-методом, с использованием симплексной таблицы. Определим максимальное значение целевой функции F(X) = 2x1+x2+3x3 при следующих условиях-ограничений.
x1+2x2+x3≤1000
3x1+5x2+2x3≤1500
x1≥100
x2≥100
x3≥200
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
1x1 + 2x2 + 1x3 + 1x4 + 0x5 + 0x6 + 0x7 + 0x8 = 1000
3x1 + 5x2 + 2x3 + 0x4 + 1x5 + 0x6 + 0x7 + 0x8 = 1500
1x1 + 0x2 + 0x3 + 0x4 + 0x5-1x6 + 0x7 + 0x8 = 100
0x1 + 1x2 + 0x3 + 0x4 + 0x5 + 0x6-1x7 + 0x8 = 100
0x1 + 0x2 + 1x3 + 0x4 + 0x5 + 0x6 + 0x7-1x8 = 200
Введем искусственные переменные x.
1x1 + 2x2 + 1x3 + 1x4 + 0x5 + 0x6 + 0x7 + 0x8 + 0x9 + 0x10 + 0x11 = 1000
3x1 + 5x2 + 2x3 + 0x4 + 1x5 + 0x6 + 0x7 + 0x8 + 0x9 + 0x10 + 0x11 = 1500
1x1 + 0x2 + 0x3 + 0x4 + 0x5-1x6 + 0x7 + 0x8 + 1x9 + 0x10 + 0x11 = 100
0x1 + 1x2 + 0x3 + 0x4 + 0x5 + 0x6-1x7 + 0x8 + 0x9 + 1x10 + 0x11 = 100
0x1 + 0x2 + 1x3 + 0x4 + 0x5 + 0x6 + 0x7-1x8 + 0x9 + 0x10 + 1x11 = 200
Для постановки задачи на максимум целевую функцию запишем так:
F(X) = 2x1+x2+3x3 — Mx9 — Mx10 — Mx11 => max
За использование искусственных переменных, вводимых в целевую функцию, накладывается так называемый штраф величиной М, очень большое положительное число, которое обычно не задается.
Полученный базис называется искусственным, а метод решения называется методом искусственного базиса.
Причем искусственные переменные не имеют отношения к содержанию поставленной задачи, однако они позволяют построить стартовую точку, а процесс оптимизации вынуждает эти переменные принимать нулевые значения и обеспечить допустимость оптимального решения.
Из уравнений выражаем искусственные переменные:
x9 = 100-x1+x6 x10 = 100-x2+x7 x11 = 200-x3+x8которые подставим в целевую функцию:
F(X) = 2x1 + x2 + 3x3 — M(100-x1+x6) — M(100-x2+x7) — M(200-x3+x8) => max
или
F(X) = (2+1M)x1+(1+1M)x2+(3+1M)x3+(-1M)x6+(-1M)x7+(-1M)x8+(-400M) => max
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
| 1 | 2 | 1 | 1 |
| 3 | 5 | 2 | 1 |
| 1 | -1 | 1 | |
| 1 | -1 | 1 | |
| 1 | -1 | 1 |
4591011
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| x4 | 1000 | 1 | 2 | 1 | 1 | ||||||||
| x5 | 1500 | 3 | 5 | 2 | 1 | ||||||||
| x9 | 100 | 1 | -1 | 1 | |||||||||
| x10 | 100 | 1 | -1 | 1 | |||||||||
| x11 | 200 | 1 | -1 | 1 | |||||||||
| Индексная строка | F(X0) | -400M | -2-1M | -1-1M | -3-1M | 1M | 1M | 1M |
Иногда такую таблицу представляют с дополнительной строкой для М.
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| x4 | 1000 | 1 | 2 | 1 | 1 | ||||||||
| x5 | 1500 | 3 | 5 | 2 | 1 | ||||||||
| x9 | 100 | 1 | -1 | 1 | |||||||||
| x10 | 100 | 1 | -1 | 1 | |||||||||
| x11 | 200 | 1 | -1 | 1 | |||||||||
| Индексная строка | F(X0) | -2 | -1 | -3 | |||||||||
| M | -400 | -1 | -1 | -1 | 1 | 1 | 1 |
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | min |
| 1 | x4 | 1000 | 1 | 2 | 1 | 1 | 1000 | |||||||
| x5 | 1500 | 3 | 5 | 2 | 1 | 750 | ||||||||
| x9 | 100 | 1 | -1 | 1 | ||||||||||
| x10 | 100 | 1 | -1 | 1 | ||||||||||
| x11 | 200 | 1 | -1 | 1 | 200 | |||||||||
| Индексная строка | F(X1) | -400M | -2-1M | -1-1M | -3-1M | 1M | 1M | 1M |
Конец итераций: индексная строка не содержит отрицательных элементов — найден оптимальный план.
Окончательный вариант симплекс-таблицы:
| План | Базис | В | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 |
| 5 | x4 | 350 | 1 | -0.5 | -0.5 | -0.5 | 0.5 | 0.5 | |||||
| x8 | 150 | 0.5 | 1.5 | 2.5 | 1 | -1.5 | -2.5 | -1 | |||||
| x1 | 100 | 1 | -1 | 1 | |||||||||
| x2 | 100 | 1 | -1 | 1 | |||||||||
| x3 | 350 | 1 | 0.5 | 1.5 | 2.5 | -1.5 | -2.5 | ||||||
| Индексная строка | F(X5) | 1350 | 1.5 | 2.5 | 6.5 | -2.5+1M | -6.5+1M | 1M |
123