Истоки математики: логические идеи

2.3Кванторы и предикаты с несколькими переменными

Связывание одной переменной

S(x,y)=x2=yxy∃xS(x,y)

Если задать конкретное значение y, например, y=4, получается такая штука:
∃xS(x,4) или попросту

∃xx2=4

4x=2

Однако, можно выбрать другое значение y, например, положить y=−1. Тогда
получается утверждение

∃xx2=−1

x−1

Вернёмся теперь к утверждению ∃xS(x,y). Мы видим, что в в это
утвреждение вместо y можно подставлять различные числа и получать разные
высказывания — верные и неверные. Значит, перед нами предикат, зависящий от y.
Обозначим его через Q(y). Можно записать:

Q(y):=(∃xS(x,y))

Syx∃xS(x,y)yx

Последовательное применение кванторов

G(n,m)=n>m
Z(m):=(∃nG(n,m))=(∃nn>m).

∀mZ(m)
∀m∃nn>m.(2.3)

mnn>m

Во-первых, нужно заметить. что получившееся утверждение не является предикатом
— мы последовательно связали обе переменные и то, что получилось, уже ни от чего
не зависит, это просто высказывание, которое может быть истинным или ложным.

Является ли оно истинным? Да, является. Действительно, возьмём любое m.
Заметим, что для него предикат Z(m) верен, поскольку существует такое n
(например, можно взять n=m+1), для которого n>m. (Действительно, m+1>m,
каким бы ни было m.)

Словами это высказывание можно было бы записать так: «для всякого натурального
числа найдётся большее его число». Эта формулировка с точки зрения привычного
нам языка выглядит немножко неестественно и может возникнуть искушение сделать
её более привычной, переформулировав таким образом:
«найдется натуральное число, большее любого другого натурального числа». Однако,
то, что в результате получилось — не переформулировка исходного утверждения, а
совсем другое высказывание. Оно формально записывается так:

∃n∀mn>m(2.4)

nmn>mnn>mmnnm=nm=n+1m=n+2n>m

Отрицание и серия кванторов

∀mn>mW(n)
¬(∃nW(n))

¬(∃nW(m))=∀n(¬W(m))=∀n(¬(∀mn>m))=…(2.5)

¬(∀mm>m)
…=(∀n∃m¬(n>m))=(∀n∃mn⩽m).

n>mn>mn⩽m
∀n∃mn⩽m.

nmn⩽mm=nm=n+1m=n+100

Разделы

В Математической предметной классификации математическая логика объединена в одну секцию верхнего уровня с основаниями математики, в которой выделены следующие разделы:

• общая логика (англ. general logic), включает классическую логику первого порядка, логики высших порядков (логику второго порядка), комбинаторную логику, λ-исчисление, временную логику, модальную логику, многозначные логики, нечёткую логику, логику в информатике;
• теория моделей;
• теория вычислимости и теория рекурсии;
• теория множеств;
• теория доказательств и конструктивная математика;
• алгебраическая логика (включает вопросы изучения булевых алгебр, алгебр Гейтинга, квантовых логик, цилиндрических и полиадических алгебр, алгебр Поста);
• нестандартные модели.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Основные равносильности алгебры высказываний

С двумя из них мы только что познакомились, но ими дело, понятно, не огранивается. Тождеств довольно много и я перечислю самые важные и самые известные из них:

Коммутативность конъюнкции и коммутативность дизъюнкции

Коммутативность – это перестановочность:

Знакомые с 1-го класса правила: «От перестановки множителей (слагаемых) произведение (сумма) не меняется». Но при всей кажущейся элементарности этого свойства, справедливо оно далеко не всегда, в частности, некоммутативным является умножение матриц (в общем случае их  переставлять нельзя), а векторное произведение векторов – антикоммутативно (перестановка векторов влечёт за собой смену знака).

И, кроме того, здесь я снова хочу подчеркнуть формализм математической логики. Так, например, фразы «Студент сдал экзамен и выпил» и «Студент выпил и сдал экзамен» различны с содержательной точки зрения, но неразличимы с позиций формальной истинности. …Таких студентов знает каждый из нас, и из этических соображений мы не будет озвучивать конкретных имён =)

Ассоциативность логического умножения и сложения

Дистрибутивные свойства

Обратите внимание, что во 2-м случае будет некорректно говорить о «раскрытии скобок», в известном смысле здесь «фикция» – ведь их можно убрать вообще: , т.к. умножение – это более сильная операция

И опять же – эти, казалось бы, «банальные» свойства выполняются далеко не во всех алгебраических системах, и, более того, требуют доказательства (о которых мы очень скоро поговорим). К слову, второй дистрибутивный закон несправедлив даже в нашей «обычной» алгебре. И в самом деле:

Закон идемпотентности

Что делать, латынь….

Прямо какой-то принцип здоровой психики: «я и я – это я», «я или я – это тоже я» =)

И тут же несколько похожих тождеств:

…мда, что-то я даже подзавис… так и доктором философии завтра можно проснуться =)

Закон двойного отрицания

Ну а здесь уже напрашивается пример с русским языком – все прекрасно знают, что две частицы «не» означают «да». А для того, чтобы усилить эмоциональную окраску отрицания нередко используют три «не»: – даже с крохотным доказательством получилось!

 – «а был ли мальчик?» =)

В правом тождестве скобки можно опустить.

Законы де Моргана

Предположим, что строгий Преподаватель (имя которого вам тоже известно:)) ставит экзамен, если  – Студент ответил на 1-й вопрос и  – Студент ответил на 2-й вопрос. Тогда высказывание , гласящее о том, что Студент не сдал экзамен, будет равносильно утверждению  – Студент не ответил на 1-й вопрос или на 2-й вопрос.

Как уже отмечалось выше, равносильности подлежат доказательству, которое стандартно осуществляется с помощью таблиц истинности. В действительности мы уже доказали равносильности, выражающие импликацию и эквиваленцию, и сейчас настало время закрепить технику решения данной задачи.

Докажем тождество . Поскольку в  него входит единственное высказывание , то «на входе» возможно всего лишь два варианта: единица либо ноль. Далее приписываем единичный столбец и применяем к ним правило И:
В результате «на выходе» получена формула, истинность которой совпадает с истинностью высказывания . Равносильность  доказана.

Да, это доказательство является примитивным (а кто-то скажет, что и «тупым»), но типичный Преподаватель по матлогике вытрясет за него душу. Поэтому даже к таким простым вещам не стОит относиться пренебрежительно.

Теперь убедимся, например, в справедливости закона де Моргана .

Сначала составим таблицу истинности для левой части. Поскольку дизъюнкция находится в скобках, то в первую очередь выполняем именно её, после чего отрицаем столбец  :
Далее составим таблицу истинности для правой части . Здесь тоже всё прозрачно – в первую очередь проводим более «сильные» отрицания, затем применяем к столбцам  правило И:
Результаты совпали, таким образом, тождество  доказано.

Любую равносильность  можно представить в виде тождественно истинной формулы . Это значит, что ПРИ ЛЮБОМ исходном наборе нулей и единиц «на выходе» получается строго единица. И этому есть очень простое объяснение: так как таблицы истинности  и  совпадают, то, разумеется, они эквивалентны. Соединим, например, эквиваленцией левую и правую часть только что доказанного тождества де Моргана:
Или, если компактнее:

Задание 2

Доказать следующие равносильности:

а) ;

б)

Краткое решение в конце урока. Не ленимся! Постарайтесь не просто составить таблицы истинности, но ещё и чётко сформулировать выводы. Как я недавно отмечал, пренебрежение простыми вещами может обойтись очень и очень дорого!

Формулы логики высказываний

Понятие логической формы сложного высказывания уточняется с помощью понятия формулы
логики высказываний.

В примерах 1 и 2 мы учились записывать с помощью логических операций сложные высказывания.
Вообще-то они называются формулами логики высказываний.

Для обозначения высказываний, как и упомянутом примере, будем продолжать использовать буквы

Эти буквы будут играть роль переменных, принимающих в качестве значений истинностные
значения «истина» и «ложь». Эти переменные называются также пропозициональными переменными. Мы будем далее
называть их элементарными формулами или атомами.

Для построения формул логики высказываний кроме указанных выше букв используются знаки
логических операций

~, ∧, ∨, →, ,

а также символы, обеспечивающие возможность однозначного прочтения формул — левая и
правая скобки.

Понятие формулы логики высказываний определим следуюшим
образом:

1) элементарные формулы (атомы) являются формулами логики высказываний;

2) если и —
формулы логики высказываний, то , ,
, ,
тоже являются формулами логики
высказываний;

3) только те выражения являются формулами логики высказываний, для которых это
следует из 1) и 2).

Определение формулы логики высказываний содержит перечисление правил образования
этих формул. Согласно определению, всякая формула логики высказываний либо есть атом, либо образуется
из атомов в результате последовательного применения правила 2).

Пример 6. Пусть — одиночное
высказывание (атом) «Все рациональные числа являются действительными», —
«Некоторые действительные числа — рациональные числа», —
«некоторые рациональные числа являются действительными». Переведите в форму словесных высказываний
следующие формулы логики высказываний:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

Решение.

1) «нет действительных чисел, которые являются рациональными»;

2) «если не все рациональные числа являются действительными, то нет рациональных чисел, являющихся действительными»;

3) «если все рациональные числа являются действительными, то некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными»;

4) «все действительные числа — рациональные числа и некоторые действительные числа — рациональные числа и некоторые рациональные числа являются действительными числами»;

5) «все рациональные числа являются действительными тогда и только тогда, когда не имеет место быть, что не все рациональные числа являются действительными»;

6) «не имеет места быть, что не имеет место быть, что не все рациональные числа являются действительными и нет действительных чисел, которые являются рациональными или нет рациональных чисел, которые являются действительными».

Пример 7. Составьте таблицу истинности для формулы
логики высказываний , которую в
таблице можно обозначить .

Решение. Составление таблицы истинности начинаем с записи значений («истина» или «ложь»)
для одиночных высказываний (атомов) , и
. Все возможные значения записываются в восемь строк таблицы. Далее,
определяя значения операции импликации, и продвигаясь вправо по таблице, помним, что значение равно «лжи» тогда, когда из «истины» следует «ложь».

И	И	И	И	И	И	И	И
И	И	Л	И	И	И	Л	И
И	Л	И	И	Л	Л	Л	Л
И	Л	Л	И	Л	Л	И	И
Л	И	И	Л	И	Л	И	И
Л	И	Л	Л	И	Л	И	Л
Л	Л	И	И	И	И	И	И
Л	Л	Л	И	И	И	Л	И

Заметим, что никакой атом не имеет вида
, ,
, ,
. Такой вид имеют сложные формулы.

Число скобок в формулах логики высказываний можно уменьшить, если принять, что

1) в сложной формуле будем опускать внешнюю пару скобок;

2) упорядочим знаки логических операций «по старшинству»:

, →, ∨, ∧, ~ .

В этом списке знак имеет самую большую область действия, а знак ~ — самую
маленькую. Под областью действия знака операции понимаются те части формулы логики высказываний, к которым
применяется (на которые действует) рассматриваемое вхождение этого знака. Таким образом, можно опускать
во всякой формуле те пары скобок, которые можно восстановить, учитывая «порядок старшинства». А при
восстановлении скобок сначала расставляются все скобки, относящиеся ко всем вхождениям знака ~ (при
этом мы продвигаемся слева направо), затем ко всем вхождениям знака ∧ и так далее.

Пример 8. Восстановите скобки в формуле логики высказываний
.

Решение. Скобки восстанавливаются пошагово следующим образом:

Не всякая формула логики высказываний может быть записана без скобок. Например, в
формулах и
дальнейшее исключение скобок
невозможно.

Формы представления функций алгебры логики

Существует три способа представления выражений:

• в виде таблицы истинности;
• аналитическая форма;
• логическая форма.

Таблица истинности 

При этом способе комбинации логических переменных они расположены в порядке возрастания их двоичного номера. Наборы переменных обозначаются числами от нуля до 2n − 1, где n – количество переменных функции. При наличии значений на всех комбинациях функция называется полностью определенной.

Пример

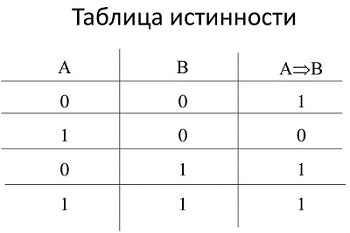
Аналитическое выражение

Рассмотрение данной формы невозможно без введения новых понятий.

• терм – компонент выражения;
• ранг терма – число переменных в терме;
• дизъюнктивный терм (макстерм) – логическое сложение произвольного количества попарно независимых переменных;
• конъюнктивный терм (минтерм) – логическое умножение произвольного количества попарно независимых переменных. 

В аналитической записи используют две формы выражения:

дизъюнктивную нормальную форму (ДНФ)

\(f(a,b,c)=\overline ab\overline c+a\overline b+a\overline c+b\)

конъюнктивную нормальную форму (КНФ)

\(f(X_1X_2X_3X_4)=(X_1+\overline{X_2}+X_3)(\overline{X_1}+\overline{X_2}+X_3+X_4)(X_1+X_2)\)

При условии, что все термы, составляющие нормальную форму, имеют одинаковый и максимальный ранг, который равен количеству переменных функции, форма называется совершенной. В такой форме минтерм – конституентная единицы, макстерм – конституентная нуля.

Совершенная дизъюнктивная форма (дизъюнкция конституент единицы) записывается так:

\(F(a,b,c)=\overline abc+abc+abc+ab\overline c\)

Совершенная конъюнктивная форма (конъюнкция конституент нуля) имеет вид:

\(F(a,b,c,d)=(a+b+\overline c+d)(\overline a+b+\overline c+d)(\overline a+\overline d+\overline c+d)\)

Аналитические формы полностью дуальны.

Числовая запись

Данный вид записи функций алгебры логики позволяет представить ее компактно.

Вид для совершенной дизъюнктивной нормальной формы:

\(f(a,b,c)=\vee(1,3,6,7)\)

Вид для совершенной конъюнктивной нормальной формы:

\(f(a,b,c)=\wedge(0,2,4,5)\)

2.1Высказывания

Примеры высказываний

Как бы определение 1. Высказывание — это утверждение с чётко определенным смыслом, которое может
быть истинным или ложным.

Как обычно, проще привести несколько примеров.

Пример.

• «2+2=5» — пример высказывания. Оно ложно.
• «3>2» — ещё один пример высказывания. Оно истинно.
• «5 — простое число» — ещё одно истинное высказывание.
• «Множество простых чисел конечно» — это ложное высказывание.
• «Если целое число простое и оно больше двух, оно нечётно» —
  истинное высказывание.
• «Каждое чётное число, большее двух, можно представить в виде суммы
  двух простых чисел» — это высказывание, истинность которого в
  настоящий момент неизвестна (это так называемая бинарная проблема
  Гольдбаха).
• «n — чётное число» — это не высказывание, потому что непонятно,
  чему равно n (здесь, конечно, под n подразумевается не
  собственно буква, а переменная, которая может принимать разные
  значения), и поэтому это утверждение не является ни ложным, ни
  истинным. С такого типа утверждениями (они называются предикатами)
  мы познакомимся чуть позже.

Вместо «истинно» или «ложно» используются и другие синонимичные выражения:
верно (неверно), корректно (некорректно) и т.д.

Операции с высказываниями

AB

Определение 1. Высказывание «верно по крайней мере одно из двух высказываний A или B (или
оба)», называется дизъюнкцией высказываний A и B. Оно
обозначается A∨B. Другой термин для дизъюнкции — логическое
«ИЛИ».

Определение 2. Высказывание «верны оба высказывания A и B» называется
конъюнкцией высказываний A и B. Оно обозначается A∧B.
Другой термин для конъюнкции — логическое «И».

Определение 3. Высказывание «высказывание A неверно» называется отрицанием A.
Обозначается ¬A. Другой термин — логическое «НЕ».

Если про каждое из высказываний A и B известно, является оно истинным или
ложным, легко установить истинность их конъюнкции, дизъюнкции и отрицания.
Например, если A истинно, то ¬A ложно. Если A и B оба истинны, то
A∧B истинно, иначе оно ложно. И так далее. Эту информацию удобно
записывать в виде табличек, которые называются таблицами истинности.

Таблица истинности для отрицания выглядит так:

A¬AИЛЛИ

ABA∨BA∧BИИИИИЛИЛЛИИЛЛЛЛЛ

Раскрытие скобок с отрицанием

AB¬(A∨B)AB
¬(A∨B)=(¬A)∧(¬B)

¬(A∧B)AB
¬(A∧B)=(¬A)∨(¬B)

∨∧

Эти правила преобразования формул в алгебре логики называются законами де
Моргана.

Замечание 1. Законы де Моргана мгновенно обобщаются на случай большего количества
высказываний. Например, ¬(A∧B∧C)=(¬A)∨(¬B)∨(¬C).

Справочная информация

ДокументыЗаконыИзвещенияУтверждения документовДоговораЗапросы предложенийТехнические заданияПланы развитияДокументоведениеАналитикаМероприятияКонкурсыИтогиАдминистрации городовПриказыКонтрактыВыполнение работПротоколы рассмотрения заявокАукционыПроектыПротоколыБюджетные организацииМуниципалитетыРайоныОбразованияПрограммыОтчетыпо упоминаниямДокументная базаЦенные бумагиПоложенияФинансовые документыПостановленияРубрикатор по темамФинансыгорода Российской Федерациирегионыпо точным датамРегламентыТерминыНаучная терминологияФинансоваяЭкономическаяВремяДаты2015 год2016 годДокументы в финансовой сферев инвестиционной

Математические задачи на логику для дошкольников

Начиная с 3 летнего возраста малыша, родители должны понемногу заниматься тренировкой логического мышления у своих детей

Детям это очень важно, ведь для них в таком возрасте многие очевидные вещи кажутся сложными, а непонятные для восприятия взрослым, напротив, очевидными. Представим несколько вариантов логических задач для детей 3-5 лет

1. На столе лежит 1 апельсин. Его разрезали на 2 части, сколько апельсинов лежит на столе? Ответ: 1, разрезанный.
2. Собаку привязали к забору веревкой. Длина веревки составляет 10 метров, а собака прошла за день 100 метров. Как ей это удалось? Ответ: Собака ходила вдоль забора туда и обратно и «находила» целых 100 метров.

3. Какой день недели соответствует числу 3? Ответ: среда, т.к. его порядковый номер в неделе – 3.

   Примечание: Про дни недели дошкольникам можно задавать различные варианты вопросов. Это поможет не только в развитии логического мышления, но и поможет скорее выучить дни недели.

4. Посчитать, сколько людей в следующей строке: ты да я, да мы с тобой. Ответ: 2.
5. Папа и сын, дедушка и внук, сын и папа. Сколько всего человек здесь отмечено? Ответ: 3, т.к. папа – сын дедушки, сын папы – внук дедушки.
6. На опушке стояло 3 высоких сосны. На каждой сосне по 3 больших ветки и по 3 маленьких. На каждой маленькой ветке по яблоку. Сколько всего яблок на деревьях? Ответ: 0, на соснах яблоки не растут.
7. Папу Антона зовут Андрей Викторович, а дедушку – Сергей Иванович. Какое отчество у мамы Антона? Ответ: Сергеевна, Потому что Сергей Иванович – это отец мамы Антона. Отца папы Антона зовут Виктор.
8. У двух братьев по одной сестре. Сколько всего детей в семье? Ответ: 3. 2 брата и одна сестра на двоих.

9. Какие камни есть в море? Ответ: мокрые.

   Примечание: аналогичная задача-загадка моет звучать так «Каких камней в море нет?» — ответ: сухих.

10. Вася и Петя играли в морской бой и сыграли по 3 партии. Каждый выиграл по 3 раза. Это правда или ложь? Ответ: ложь. Во время одной партии выиграть может только один.
11. В поле работали 5 тракторов. 2 трактора сломались и остановились. Сколько тракторов в поле? Ответ: 5, т.к. учитываются все тракторы, и рабочие, и сломанные.
12. Одно яйцо варится 5 минут. Сколько времени нужно, чтобы сварить 2 яйца? Ответ: все те же 5 минут.
13. Саша сидит в самолете. Впереди него машина, сзади – лошадь. Где находится Саша? Ответ: катается на карусели.
14. Алена сидит, когда она встанет и уйдет, ее мама так и не сможет сесть на ее место. Где сидит Алена? Ответ: у мамы на коленях.
15. Что все дети на земле делают одновременно? Ответ: взрослеют.

Опираясь на предложенные варианты заданий на развитие логического мышления, родители могут придумывать незамысловатые условия задач самостоятельно.

2.4Импликация

AQ(n)nE(n)n∀nQ(n)E(n)

Вероятно, здесь проще начать с отрицания. Что нам нужно было бы сделать, чтобы
опровергнуть утверждение A? Нужно придумать такое n, чтобы оно делилось на
4, но при этом не делилось на 2. Именно такой контрпример, если бы он
был построен, опроверг бы наше утверждение. Иными словами, нам нужно было бы
предъявить такое n, что Q(n) выполняется, а E(n) нет, то есть верно
утверждение Q(n)∧(¬E(n)). Итак, отрицание к A
выглядит так:

¬A=(∃nQ(n)∧(¬E(n)))

A=(∀n(¬Q(n))∨E(n))(2.6)

n¬Q(n)¬Q(n)E(n)

Это ровно то, что мы хотим сказать.

Вопрос 2. Зачем городить такой огород? Почему нельзя было просто написать
∀nP(n)∧Q(n)?(2.7)

  Можно было так и написать, формулы и
эквивалентны.

А вот и нет. Например, утверждение A и формула
являются истинными, а утверждение в формуле
ложно. Действительно, возьмём, например,
n=6. Оно не делится на 4, значит, Q(6) ложно, и значит для
этого значения n конъюнкция ложна, а раз такое n нашлось, то
и всё утверждение ложно. Проверьте, что этот пример не
опровергает утверждение .

  Потому что это совсем другое утверждение, оно не эк��ивалентно A.

Так и есть. Например, утверждение A и формула
являются истинными, а утверждение в формуле
ложно. Действительно, возьмём, например,
n=6. Оно не делится на 4, значит, Q(6) ложно, и значит для
этого значения n конъюнкция ложна, а раз такое n нашлось, то
и всё утверждение ложно. Проверьте, что этот пример не
опровергает утверждение .

В общем виде это формулируется так. Пусть есть два высказывания, A и B.
Утверждения «из A следует B» или «A влечёт B» или «если A
истинно, то B тоже истинно», формально записываются так: ¬A∨B. Иными словами, говоря «если A истинно, то B тоже истинно», мы
говорим, что A может и не быть истинным, но нас этот случай, не интересует, мы
про него никаких выводов не делаем (а значит, и ошибаться не можем), но если уж
A истинно, то B обязано быть истинным.

Эта операция с высказываниями A и B настолько важна, что хотя она и
выражается через конъюнкцию, дизъюнкцию и отрицание, у него есть специальное
название — импликация (ср. с английским словом imply, влечёт), и
специальное обозначение: A⇒B. Утверждение A называется
посылкой, а утверждение B — заключением.

Давайте построим таблицу истинности для A⇒B (то есть ¬A∨B).

ABA⇒BИИИИЛЛЛИИЛЛИ

A⇒BABAB

Возвращаясь к примеру, который мы разбирали раньше: «если число n делится на
4, то оно чётное». Рассмотрим число n=6. Для него посылка оказалась ложной
(оно не делится на 4), и хотя заключение оказалось истинным (оно чётно), это
никак не противоречит нашей импликации: она остаётся верна и в этом случае.

В дальнейшм мы будем постоянно пользоваться импликацией в доказательствах.
Начнём прямо со следующей лекции.

Заключение… Пока что

Как мы увидели, общие попытки в этот период заключались в том, чтобы выработать способ мышления о логике. У Лейбница было видение — хотя и неполное — универсального исчисления, основанного на языке предикатов субъекта, Ричери использовал философский подход для классификации утверждений и доказуемости, а Ламберт ввел систему обозначений для представления логических идей. Первый и последний опирались на аналогию с арифметикой, в которой утверждения и выводы были представлены числами и операциями, соответственно. В частности, метод Ламберта напоминает раннюю диаграмму Венна в символической форме, хотя он думал о своих объектах как об объединениях, обладающих несколькими качествами, а не как наборах, обладающих несколькими элементами.

Не удивительно, что на этом история не закончилась! Спустя примерно 60 лет после попыток Ламберта систематизировать логику, Огастес де Морган написал свою «Формальную логику» (с более понятным названием «Исчисление умозаключений») с теми же целями, что и его предшественники. В этой публикации 1847 года де Морган прояснил, по крайней мере, некоторую путаницу, формализовав понятия Лейбница о «универсальном» и «частном» путем введения «количественного определения» в его исчисление. Вот фрагмент из его письма на эту тему, в котором слово «количество» используется, чтобы провести различие между универсальным и частным.