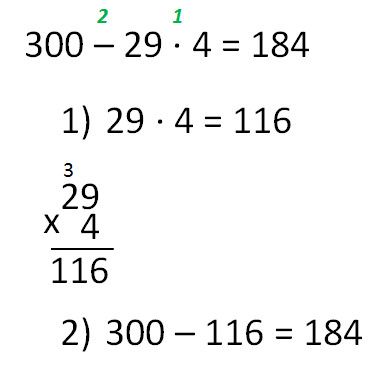Сокращенное умножение: правила, формулы

Правила раскрытия скобок

Если перед скобкой стоит знак плюс, то скобка просто снимается, выражение в ней при этом остается неизменным. Иначе говоря: 

\((a-b)=a-b\)

Здесь нужно пояснить, что в математике для сокращения записей принято не писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа, к примеру, семь и три, то пишем не \(+7+3\), а просто \(7+3\), несмотря на то, что семерка тоже положительное число. Аналогично если вы видите, например, выражение \((5+x)\) – знайте, что перед скобкой стоит плюс, который не пишут.

Пример. Раскройте скобку \((1+y-7x)\).Решение: \((1+y-7x)=1+y-7x\).

Пример. Упростите выражение: \(3+(5-2x)\).Решение: Раскрываем скобку согласно правилу, а затем приводим подобные слагаемые

Пример. Раскройте скобку и приведите подобные слагаемые: \((x-11)+(2+3x)\).Решение: \((x-11)+(2+3x)=x-11+2+3x=4x-9\).

Если перед скобкой стоит знак минус, то при снятии скобки каждый член выражения внутри нее меняет знак на противоположный:

\(-(a-b)=-a+b\)

Здесь нужно пояснить, что у \(a\), пока оно стояло в скобке, был знак плюс (просто его не писали), и после снятия скобки этот плюс поменялся на минус.

Пример: Упростите выражение \(2x-(-7+x)\).Решение: внутри скобки два слагаемых: \(-7\) и \(x\), а перед скобкой минус. Значит, знаки поменяются – и семерка теперь будет с плюсом, а икс – с минусом. Раскрываем скобку и приводим подобные слагаемые.

Пример. Раскройте скобку: \(-(4m+3)\).Решение: \(-(4m+3)=-4m-3\).

Пример. Раскройте скобку и приведите подобные слагаемые \(5-(3x+2)+(2+3x)\).Решение: \(5-(3x+2)+(2+3x)=5-3x-2+2+3x=5\).

Если перед скобкой стоит множитель, то каждый член скобки умножается на него, то есть: 

\(c(a-b)=ca-cb\)

Пример. Раскройте скобки \(5(3-x)\).Решение: В скобке у нас стоят \(3\) и \(-x\), а перед скобкой — пятерка. Значит, каждый член скобки умножается на \(5\) — напоминаю, что знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример. Раскройте скобки \(-2(-3x+5)\).Решение: Как и в предыдущем примере, стоящие в скобке \(-3x\) и \(5\) умножаются на \(-2\).

Пример. Упростить выражение: \(5(x+y)-2(x-y)\).Решение: \(5(x+y)-2(x-y)=5x+5y-2x+2y=3x+7y\).

Осталось рассмотреть последнюю ситуацию.

При умножении скобки на скобку, каждый член первой скобки перемножается с каждым членом второй:

\((c+d)(a-b)=c·(a-b)+d·(a-b)=ca-cb+da-db\)

Задания для самостоятельного решения

Задание 1. Решить уравнение:

Решение:

Ответ: 2; −2.

Задание 2. Решить уравнение:

Решение:

Ответ: корней нет.

Задание 3. Решить уравнение:

Решение:

Ответ: 3; −3.

Задание 4. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 3; −13.

Задание 5. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 12; 4.

Задание 6. Решить уравнение, используя выделение полного квадрата:

Решение:

Ответ: 7; 5.

Задание 7. Решить уравнение:

Решение:

Ответ: 0; 1.

Задание 8. Решить уравнение:

Решение:

Ответ: 0; −3.

Задание 9. Решить уравнение:

Решение:

Ответ: 7; −7.

Задание 10. Решить уравнение:

Решение:

Ответ:

Задание 11. Решить уравнение:

Решение:

Ответ: 5; −5.

Задание 12. Решить уравнение:

Решение:

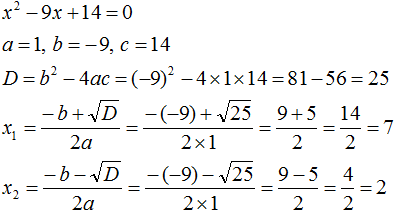
Ответ: 7; 2

Задание 13. Решить уравнение:

Решение:

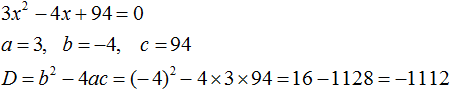
Ответ: корней нет.

Задание 14. Решить уравнение:

Решение:

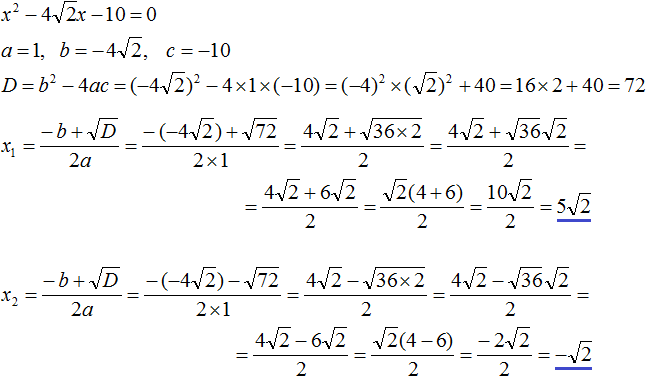
Ответ:

Задание 15. Решить уравнение:

Решение:

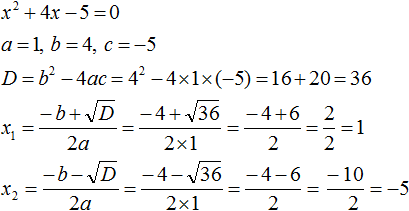
Ответ: 1; −5.

Задание 16. Решить уравнение:

Решение:

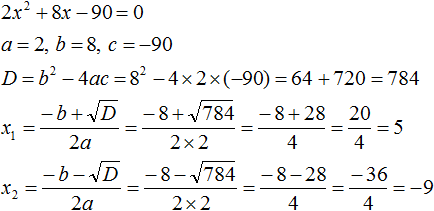
Ответ: 5; −9.

Задание 17. Решить уравнение:

Решение:

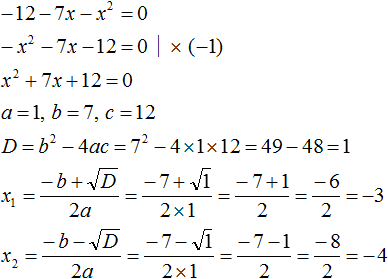
Ответ: −3; −4.

Задание 18. Решить уравнение:

Решение:

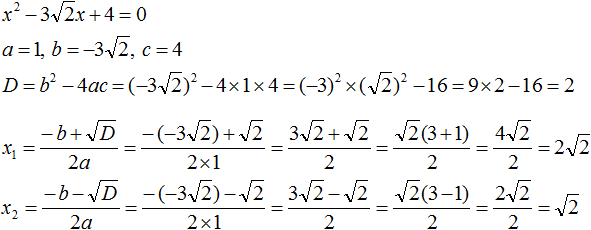
Ответ: .

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Степень разности

      Если в формулах из Таблицы 1 заменить  y  на  – y ,  то мы получим группу формул «Степень разности» (Таблица 2.):

      Таблица 2. – Степень разности

Название формулы	Формула
Квадрат (вторая степень)разности	(x – y)2 = x2 – 2xy + y2
Куб (третья степень) разности	(x – y)3 = x3 – 3x2y + 3xy2 – y3
Четвертая степень разности	(x – y)4 = x4 – 4x3y + 6x2y2 – 4xy3 + y4
Пятая степень разности	(x – y)5 = x5 – 5x4y + 10x3y2 – 10x2y3 + 5xy4– y5
Шестая степень разности	(x – y)6 = x6 – 6x5y + 15x4y2 – 20x3y3 + 15x2y4 – 6xy5 + y6
…	…

Квадрат (вторая степень) разности (x – y)2 = x2 – 2xy + y2

Куб (третья степень) разности (x – y)3 == x3 – 3x2y + 3xy2 – y3

Четвертая степень разности (x – y)4 = x4 – 4x3y ++ 6x2y2 – 4xy3 + y4

Пятая степень разности (x – y)5 = x5 – 5x4y ++ 10x3y2 –– 10x2y3 ++ 5xy4– y5

Шестая степень разности (x – y)6 = x6 – 6x5y ++ 15x4y2 –– 20x3y3 ++ 15x2y4 – 6xy5 + y6

…

Применение формул сокращенного умножения для разложения многочленов на множители

Рассмотрим тождество, которое называют разностью квадратов двух выражений:

a2–b2=(a–b)(a+b)

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы. Эту формулу применяют для разложения на множители многочлена, содержащего разность квадратов. Рассмотрим на примерах.

Пример №9. Разложить на множители многочлен 100–с2. Из условия видно, что число 100 – это квадрат числа 10,  следовательно, 100–с2=102–с2, значит можно разложить на множители по формуле: 100–с2=102–с2=(10–с)(10+с). Выделенное жирным шрифтом выражение можно не записывать, а выполнять устно.

Пример №10. Разложить на множители: х2у2–81=(ху–9)(ху+9). В данном выражении выполнено всё в соответствии с формулой, промежуточные записи не использованы.

Пример №11. Представим в виде произведения: х4–36=(х2–6)(х2+6). В данном выражении мы видим, что степень переменной может быть не только вторая, но и любая четная, чтобы ее можно было представить в виде квадрата переменной.

Пример №12. Представим в виде произведения х10с6–25=(х5с3–5)(х5с3+5). Здесь показаны разные четные степени переменных.

 Для разложения на множители суммы и разности кубов существуют определенные правила и формулы.

Сумма и разность кубов

Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности:

a3+b3=(a+b)(a2–ab+b2)

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

a3–b3=(a–b)(a2+ab+b2)

Пример №13. Разложим на множители многочлен 8+с3. В данном случае мы видим число 8, которое нужно представить в виде куба числа, это будет 23. Значит, 8+с3=23+с3. Далее распишем по формуле суммы кубов: 8+с3=23+с3=(2+с)(4–2с+с2).

Пример №14. Запишем в виде произведения разность х3–а12. В этом выражении есть степень, отличная от третьей, поэтому представим а12 в виде куба числа (а4)3. Получим: х3–а12=х3–(а4)3. Разложим на множители по формуле разности кубов: х3–а12=х3–(а4)3=(х–а4)(х2+ха4+а8).

Разложение многочлена формулой квадрата суммы и разности

Формулы квадрата суммы и квадрата разности также используют для разложения многочлена на множители. Для этого формулы записываются в обратном порядке, то есть меняются левая и правая части местами:

a2+2ab+b2=(a+b)2

a2–2ab+b2=(a–b)2

Пример №15. Преобразовать трехчлен 4х2+12х+9 в квадрат двучлена. Для этого определим, где здесь числа, которые можно представить в виде квадрата, это будут 4х2 и 9, так как 4х2=(2х)2, а 9=32. Соответственно проверим, является ли 12х удвоенным произведением чисел 2х и 3: 22х3=12х. Выполняем запись: 4х2+12х+9=(2х)2+2•2х•3+32=(2х+3)2. Обычно промежуточное действие (выделено жирным) не записывается, квадраты чисел определяются устно.

Пример №16. Разложить на множители многочлен –16с+с2+ Определяем, где здесь квадраты чисел – это с2 и 64=82. Слагаемое –16с не может быть квадратом числа, так как оно отрицательное и степень числа с первая, поэтому –16с это удвоенное произведение чисел с и 8. Выполняем разложение на множители: –16с+с2+64=(с–8)2

Обратим внимание на тот момент, что числа с и 8 можно записывать наоборот в ответе, так как квадраты противоположных чисел равны, то есть –16с+с2+64=(8–с)2

Урок двадцать третий. Правило квадрата шахматной пешки.

crash птн, 07/03/2015 — 15:10

Пройдет ли шахматная пешка в ферзи?

Сегодня король находится достаточно далеко от своей пешки и не успевает ей помочь. Теперь всё зависит от того, где расположен король противника, и далеко ли от поля превращения находится пешка. Большое значение имеет и очередь хода.Пешка бежит в ферзи, а король чёрных стремится задержать её. Начинающий тыкает пальцами во все клетки: «Я сюда, он туда, я сюды, он туды!» При таком подсчёте случаются ошибки.Выучи правило, которое поможет тебе сразу определить, как закончится борьба в этом окончании. Называется оно правило квадрата пешки.

Сначала построим квадрат, сторона которого будет равна количеству клеток от пешки до поля превращения, включая и то поле, на котором находится пешка. Для белой пешки h4 квадратом станет h4 – h8 – d8 – d4.

Если король слабейшей стороны находится в квадрате пешки или при своём ходе попадает в него, то он задерживает пешку.Получается, что при своём ходе король попадает в квадрат, успеет задержать пешку и уничтожить её. При ходе белых – пешка успеет стать ферзём. Проверим, так ли это на самом деле. Но надо учитывать, что квадрат уменьшается по мере продвижения пешки.Итак, при ходе1. h4–h5 Kpc4–d52. h5–h6 Kpd5–e63. h6–h7 Kpe6–f74. h7–h8Ф.Чёрный король со всех ног бежал, но так и не успел догнать пешку. Она проскакивает в ферзи.

Гораздо труднее придётся белым, если не они ходят первыми

В этом окончании надо сразу обратить внимание на то, как при движение пешки меняется (уменьшается) КВАДРАТ.1

. . Kpc4 – d4!Король сразу попадает в квадрат пешки. Квадрат пока большой 5 на 5.2. h4 – h5 Kpd4 – e5

Теперь король по диагонали после каждого хода впрыгивает в квадрат ускользающей пешки.3. h5 – h6 Kpe5 – f6После последнего хода квадрат уже стал 3 на 3. Король в квадрате, и он успевает догнать пешку.

4. h6 – h7 Kpf6 – g75. h7 – h8Ф+ Kpg7 : h8Королевская погоня закончилась в квадрате 1 на 1. Пешка уничтожена.

Строя квадрат, учитывай, где находится пешка. Легко ошибиться, определяя границы пешки как g2–g8.Если пешка стоит на 2-й горизонтали, считай что она уже на 3-й линии. Первый ход пешка может сделать на две клетки! Для пешки, стоящей на а2, квадрат (a3 – a8 – f3 – f8). Понятно, что король, даже при своём ходе, не попадает в квадрат белой пешки.

Внимательно посмотри, встретится ли на пути короля, который стремится в квадрат пешки, какое-либо препятствие? Тогда его придётся обходить, и можно не успеть оказаться у цели. Кажется, что наш король первым ходом попадает в квадрат пешки d4(d4 – d1 – g4 – g1).

Но неожиданно король встречает препятствие в виде своей же пешки f3, которую приходится обходить, теряя темпы. Как хотелось бы пешку съесть!

На тему «квадрата» посмотри позицию этюдиста Л. Прокеша.1. Kpd8 – c8! Kpd6 – c6Куда идёт король? Почему он удаляется от опасной проходной пешки? Хочется, но нельзя королю в другую сторону1. Kpd8–e8? h7–h5 2. Kpe8–f7 h5–h4 3. a5–a6 Kpd6–c6 4. a6–a7 Kpc6–b7.Оказывается, король помог своей пешке.2. Kpc8 – b8! Kpc6 – b5Вновь король удаляется от опасной проходной. Чёрный король вынужден подняться вверх, уступая горизонталь – поле b6 под контролем пешки.3. Kpb8 – b7 Kpb5 : a5А бить пешку чёрный король был вынужден. Белый король поднимается на освободившуюся линию. А чёрный король уступил ему дорогу.4. Kpb7 – c6 h7 – h5Теперь белый король в «квадрате пешки» h7, несмотря на её длинный прыжок.5. Kpc6 – d5 h5 – h4 6. Kpd5 – e4 h4 – h3 7. Kpe4 – f3 h3 – h2 8. Kpf3 – g2.Вот таким обманным движением белый король и решил свою задачу

Обрати внимание, что горизонтали белый король не проигрывал

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Всего их пять штук — ниже мы их рассмотрим.

Мы будем употреблять такие понятия, как натуральные числа, целые числа, рациональные числа, иррациональные числа. Чтобы не запутаться, дадим им определение:

Натуральные числа — это числа, которые мы используем, чтобы считать предметы: раз банан, два банан.

• Целые числа — это все натуральные числа, натуральные со знаком минусом (-1, -2, -3) и число 0.
• Рациональными называют дробные числа (1/2;1/3;1/5)
• Иррациональные числа — это бесконечная десятичная дробь. Например, число «пи» как раз такое — 3,141592…

Все, теперь мы точно готовы разбираться со свойствами степеней. Поехали!

Разность квадратов

Итак, мы разобрались с ситуациями произведения двух скобок с плюсом в них и двух скобок с минусом. Остался случай произведения одинаковых скобок с разными знаками. Смотрим, что получится:

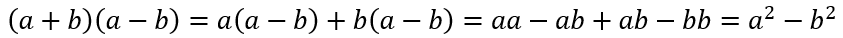
Получили формулу:

Разность квадратов \(a^2-b^2=(a+b)(a-b)\)

Эта формула одна из наиболее часто применяемых при разложении на множители и работе с алгебраическими дробями. 

Пример. Сократите дробь \(\frac{x^2-9}{x-3}\).

Решение:

\(\frac{x^2-9}{x-3}\)\(=\)		Да, я знаю, что рука так и тянется сократить иксы и девятку с тройкой – однако так делать ни в коем случае нельзя, ведь и в числителе, и в знаменателе стоит минус! Попробуем воспользоваться формулой.
\(=\) \(\frac{x^2-3^2}{x-3}\)\(=\)\(\frac{(x+3)(x-3)}{x-3}\)\(=\)		Вот теперь все плюсы и минусы попрятались в скобки, и значит без проблем можем сокращать одинаковые скобки.
\(=x+3\)		Готов ответ.

Ответ: \(x+3\).

Пример.Разложите на множители \(25x^4-m^{10} t^6\). Решение:

\(25x^4-m^{10} t^6\)		Воспользуемся формулами степеней: \((a^n )^m=a^{nm}\) и \(a^n b^n=(ab)^n\).
\(=(5x^2 )^2-(m^5 t^3 )^2=\)		Ну, а теперь пользуемся формулой \(a^2-b^2=(a+b)(a-b)\), где \(a=5x^2\) и \(b=m^5 t^3\).
\(=(5x^2-m^5 t^3 )(5x^2+m^5 t^3 )\)		Готов ответ.

Это три основные формулы, знать которые нужно обязательно! Есть еще формулы с кубами (см. выше), их тоже желательно помнить либо уметь быстро вывести. Отметим также, что в практике часто встречаются сразу несколько таких формул в одной задаче – это нормально. Просто приучайтесь замечать формулы и аккуратно применяйте их, и все будет хорошо.

Пример (повышенной сложности!).Сократите дробь \(\frac{x^2-4xy-9+4y^2}{x-2y+3}\) . Решение:

\(\frac{x^2-4xy-9+4y^2}{x-2y+3}\)\(=\)		На первый взгляд тут тихий ужас и сделать с ним ничего нельзя (вариант «лечь и помереть» всерьез не рассматриваем). Однако давайте попробуем поменять два последних слагаемых числителя местами и добавим скобки (просто для наглядности).
\(\frac{(x^2-4xy+4y^2)-9}{x-2y+3}\)\(=\)		Теперь немного преобразуем слагаемые в скобке: \(4xy\) запишем как \(2·x·2y\), а \(4y^2\) как \((2y)^2\).
\(\frac{(x^2-4xy+(2y)^2)-9}{x-2y+3}\)\(=\)		Теперь приглядимся – и заметим, что в скобке у нас получилась формула квадрата разности, у которой \(a=x\), \(b=2y\). Сворачиваем по ней к виду скобки в квадрате. И одновременно представляем девятку как \(3\) в квадрате.
\(\frac{(x-2y)^2-3^2}{x-2y+3}\)\(=\)		Еще раз внимательно смотрим на числитель… думаем… думаем… и замечаем формулу разности квадратов, у которой \(a=(x-2y)\), \(b=3\). Раскладываем по ней к произведению двух скобок.
\(\frac{(x-2y-3)(x-2y+3)}{x-2y+3}\)\(=\)		И вот теперь сокращаем вторую скобку числителя и весь знаменатель.
\(x-2y-3\)		Готов ответ.

Интересное о квадрате

Самое популярное словосочетание, которое приходит в голову о нашем главном герое — «Черный Квадрат».

Картина Малевича до сих пор очень популярна

Сам автор после ее создания долго мучился вопросом о том, что же это такое, и почему простой черный квадрат на белом фоне так притягивает внимание к себе

Но если вы приглядитесь внимательно, то заметите, что плоскость квадрата не гладкая, а в трещинах черной краски есть множество разноцветных оттенков. Видимо, вначале была некая композиция, которая автору не понравилась, и он закрыл ее от наших глаз этой фигурой. Черный квадрат, как ничто — черная дыра, только магической квадратной формы. А пустота, как известно, притягивает…

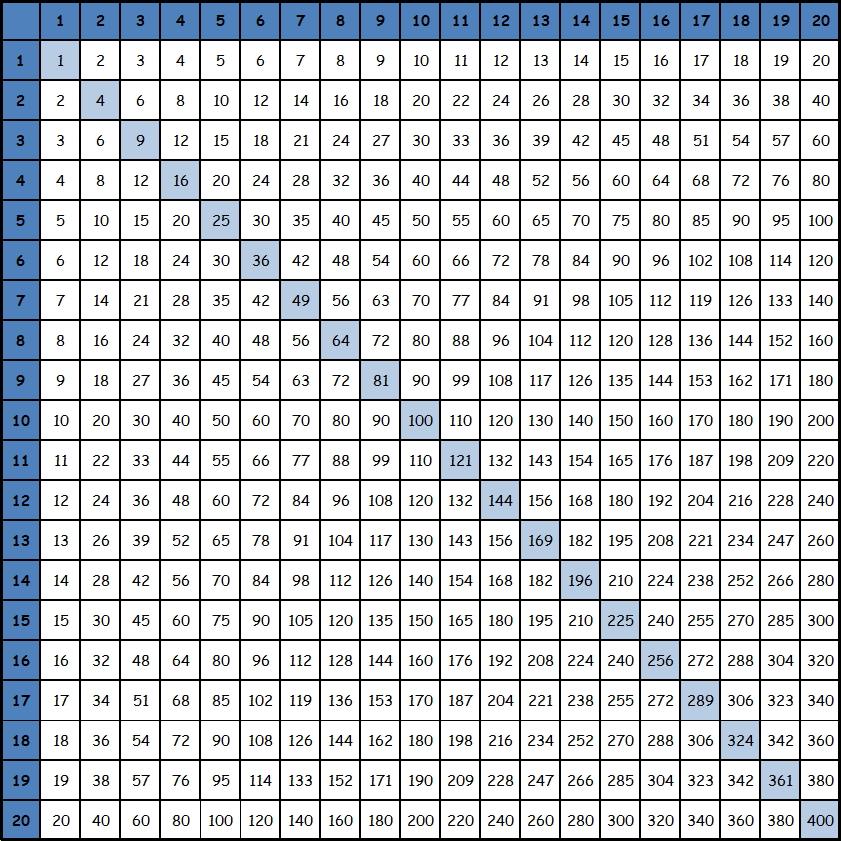
Еще очень популярны «магические квадраты». По сути это — таблица, естественно, квадратная, заполненная числами в каждой графе. Сумма этих чисел одинакова во всех строках, столбцах и диагоналях (по отдельности). Если диагонали исключаются из равенства, то квадрат – полумагический.

Альбрехт Дюрер в 1514 году создал картину «Меланхолия I», на которой изобразил магический квадрат 4х4. В нем сумма чисел всех столбцов, строк, диагоналей и даже внутренних квадратов равна тридцати четырем.

На базе этих таблиц появились очень интересные и популярные головоломки — «Судоку».

Египтяне первыми стали проводить линии взаимосвязи чисел (дата рождения) и качеств характера, способностей и талантов человека. Пифагор взял эти знания, несколько переработал и поместил в квадрат. Получился Квадрат Пифагора.

Это уже отдельное направление в нумерологии. Из даты рождения человека путем сложений высчитывают четыре основных числа, которые помещают в психоматрицу (квадрат). Так и раскладывают все тайные сведения о вашей энергии, здоровье, таланте, удаче, темпераменте и прочем по полочкам. В среднем, по опросам достоверность составляет 60%-80%.

Что такое степень числа

Алгебра дает нам такое определение: 

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

an — степень, где

a — основание степени

n — показатель степени

Соответственно, an= a·a·a·a…·a

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:

23 = 2·2·2, где

2 — основание степени

3 — показатель степени

Действия, конечно, можно выполнять и на калькуляторе — вот несколько подходящих:

• Раз
• Два
• Три

Квадрат Декарта для принятия решений в личной жизни – 3 примера

Пример 1

Жизненная ситуация – мужу предложили высокооплачиваемую работу в другом городе. Значит, нужно переезжать всей семьей.

Вопрос 1. Что будет, если мы переедем? Вырастет уровень нашей жизни; Купим машину, о которой давно мечтали. Надо искать квартиру; Надо искать садик для ребенка; Менять работу жене;	Вопрос 2. Что будет, если мы не переедем? Сохранится спокойствие и не будет страхов; Муж будет сомневаться, почему не рискнул; Ребенок пойдет в школу со своими друзьями из садика; Не купим машину, или же будем брать опять кредит.
Вопрос 3. Что не будет, если мы переедем? Возможностей карьерного роста для мужа; Возможностей для ребенка в большом городе; Спокойствия жене по поводу поиска работы; Переживаний за будущее.	Вопрос 4. Что не  будет, если мы не переедем? Новой карьеры у мужа; Новой карьеры у жены (возможно); Хлопот по поводу переезда; Возросших возможностей для ребенка.

Однако нужно понимать, что взгляд на ситуацию может абсолютно противоположный. Только заполняя собственноручно, можно получить подсказку, как действовать дальше.

Возможно, Вам будет интересно почитать, как избавиться от стресса.

Пример 2

Применение квадрата Декарта именно в личной жизни, для принятия решений.

Есть отношения, но они уже не приносят удовлетворения сегодня и не несут надежды в будущее. А время проходит, получается сегодня кое-как и завтра также. Стоит жизненный выбор – оставить партнера или нет. Вроде бы все перепробовано за ближайшие года: и примирения и отпуска вместе, но ни туда, ни сюда.

Вопрос 1.  Что будет, если мы расстанемся?

• Спокойствие;
• Возможность встречаться без ревности с друзьями;
• Появится свобода, не надо отчитываться по каждому шагу;
• Страх одиночества;

Вопрос 2. Что будет, если мы не расстанемся?

• Скандалы продолжатся;
• Потеря времени и нервов;
• Может, все же, создадим семью?
• Заведем кошку;

Вопрос 3. Что не будет, если мы расстанемся?

• Веселых плясок среди ночи;
• Экстремального отпуска;
• Эмоциональных качелей: «то ненавижу», «то люблю»;
• Синяков под глазами из-за бессонных ночей.

Вопрос 4. Что не  будет, если мы не расстанемся?

• Возможности завести нормальную семью;
• Взаимного уважения;
• Друзей;
• Надежды на «человеческие» отношения.

По теме можно почитать:

• Как простить обиду;
• Научиться мыслить позитивно.

Пример 3

Брать ипотеку или не брать. Такой вопрос часто возникает в семьях. Решение бывает нелегким, надо взвесить все плюсы и минусы. Причем, в каждой семье, это будет свои ответы. Этот выбор дан для примера, но ни в коем случае, ни кого не убеждает в необходимости пойти таким путем.

Вопрос 1.  Что будет, если возьмем ипотеку? У нас появится своя квартира; Мы перестанем снимать жилье; У нас появиться возможность создавать уют на наш вкус, не озираясь на хозяев; Платеж будет составлять всю зарплату мужа.	Вопрос 2. Что будет, если не возьмем? Будем жить на съемной квартире до старости; Хозяева будут приезжать и контролировать нас; Мы не сможем завести собаку; Риск того, что хозяева приедут и скажут «все выезжайте»; Можно позволить жить на широкую ногу, ходить в рестораны и отдыхать на море.
Вопрос 3. Что не будет, если возьмем ипотеку? Мы не сможет много лет ездить в отпуск на Багамы; У нас не получится ходить в рестораны, когда захочется; Мы не сможем менять шмотки, каждую неделю покупая новые; Не будет платить деньги на съем жилья;	Вопрос 4. Что не  будет, если мы не возьмем ипотеку? Не будем экономить на путешествиях; Возможности делать ремонт на съемной квартире на свой вкус; Не будет уюта, собаки, и возможно, второго ребенка; У нас не будет собственной квартиры.

Потренироваться можно на более простых примерах. Сознательно не стала описывать все вопросы и ответы, чтобы дать простор фантазии. Ориентируйтесь на первые 3 образца, или ниже есть еще один личный пример.

Пример 4

Предположим, давно обещали детям взять кошечку, но сомнения одолевают. Взвесьте все «За» и «Против», примените квадрат Декарта

Пример 5

Возможно, третий год собираетесь получить второе высшее образование, но что-то все время сдерживает. Помогите себе, составьте квадрат Декарта для принятия решения. Вполне вероятно, что подсознание останавливало от этого шага не зря.

Не поленитесь, потренируйтесь на данных примерах, или же сразу приступайте к поиску выбора в своей жизненной ситуации.  Разложив по полочкам ответы на вопросы в личной жизни, Вы получите ясное видение своих дальнейших шагов.

По теме можно почитать:

• Как стать успешным;
• Мотивация на каждый день.

В реальных цифрах

График функции квадрата y = x 2 представляет собой параболу .

Операция возведения в квадрат определяет реальную функцию, называемую функцией квадрата или функцией возведения в квадрат . Его доменом является вся вещественная линия , а его изображением — набор неотрицательных действительных чисел.

Функция квадрата сохраняет порядок положительных чисел: большие числа имеют большие квадраты. Другими словами, квадрат — это монотонная функция на интервале . Таким образом, нулевой является (глобальный) минимальная квадратной функции. Квадрат х 2 в А число x меньше x (то есть x 2 < x ) тогда и только тогда, когда 0 < x <1 , то есть если x принадлежит открытому интервалу (0,1) . Это означает, что квадрат целого числа никогда не меньше исходного числа x .

Каждое положительное действительное число представляет собой квадрат ровно двух чисел, одно из которых строго положительное, а другое — строго отрицательное. Ноль — это квадрат только одного числа. По этой причине можно определить функцию квадратного корня , которая связывает неотрицательное действительное число с неотрицательным числом, квадрат которого является исходным числом.

Из отрицательного числа в системе действительных чисел нельзя извлечь квадратный корень , потому что квадраты всех действительных чисел неотрицательны . Отсутствие действительных квадратных корней для отрицательных чисел можно использовать для расширения действительной системы счисления до комплексных чисел , постулируя мнимую единицу i , которая является одним из квадратных корней из −1.

Свойство «каждое неотрицательное действительное число является квадратом» было обобщено до понятия действительного замкнутого поля , которое является упорядоченным полем , в котором каждый неотрицательный элемент является квадратом и каждый многочлен нечетной степени имеет корень. Вещественные замкнутые поля нельзя отличить от поля действительных чисел по их алгебраическим свойствам: каждое свойство действительных чисел, которое может быть выражено в логике первого порядка (что выражается формулой, в которой переменные, которые количественно определяются как by или представляют элементы, а не множества), верно для каждого реального закрытого поля, и, наоборот, каждое свойство логики первого порядка, которое верно для конкретного реального закрытого поля, также верно для действительных чисел.

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Примеры решения задач

Предстáвим, что возникла необходимость построить небольшую комнату, площадь которой 8 м2. При этом длина комнаты должна быть в два раза больше её ширины. Как определить длину и ширину такой комнаты?

Сделаем примерный рисунок этой комнаты, который иллюстрирует вид сверху:

Обозначим ширину комнаты через x. А длину комнаты через 2x, потому что по условию задачи длина должна быть в два раза больше ширины. Множитель 2 и выполнит это требование:

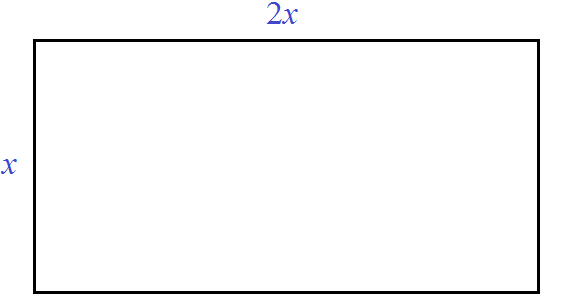
Поверхность комнаты (её пол) является прямоугольником. Для вычисления площади прямоугольника, нужно длину данного прямоугольника умножить на его ширину. Сделаем это:

2x × x

По условию задачи площадь должна быть 8 м2. Значит выражение 2x × x следует приравнять к 8

2x × x = 8

Получилось уравнение. Если решить его, то можно найти длину и ширину комнаты.

Первое что можно сделать это выполнить умножение в левой части уравнения:

2×2 = 8

В результате этого преобразования переменная x перешла во вторую степень. А мы говорили, что если переменная, входящая в уравнение, возведенá во вторую степень (в квадрат), то такое уравнение является уравнением второй степени или квадратным уравнением.

Для решения нашего квадратного уравнения воспользуемся изученными ранее тождественными преобразованиями. В данном случае можно разделить обе части на 2

Теперь воспользуемся квадратным корнем. Если x2 = 4, то . Отсюда x = 2 и x = −2.

Через x была обозначена ширина комнаты. Ширина не должна быть отрицательной, поэтому в расчёт берём только значение 2. Такое часто бывает при решении задачи, в которых применяется квадратное уравнение. В ответе получаются два корня, но условию задачи удовлетворяет только один из них.

А длина была обозначена через 2x. Значение x теперь известно, подставим его в выражение 2x и вычислим длину:

2x = 2 × 2 = 4

Значит длина равна 4 м, а ширина 2 м. Это решение удовлетворяет условию задачи, поскольку площадь комнаты равна 8 м2

4 × 2 = 8 м2

Ответ: длина комнаты составляет 4 м, а ширина 2 м.

Пример 2. Огородный участок, имеющий форму прямоугольника, одна сторона которого на 10 м больше другой, требуется обнести изгородью. Определить длину изгороди, если известно, что площадь участка равна 1200 м2

Решение

Длина прямоугольника, как правило, больше его ширины. Пусть ширина участка x метров, а длина (x + 10) метров. Площадь участка составляет 1200 м2. Умножим длину участка на его ширину и приравняем к 1200, получим уравнение:

x(x + 10) = 1200

Решим данное уравнение. Для начала раскроем скобки в левой части:

Перенесём 1200 из правой части в левую часть, изменив знак. В правой части останется

Решим получившееся уравнение с помощью формул:

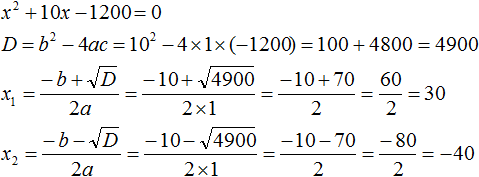
Несмотря на то, что квадратное уравнение имеет два корня, в расчёт берём только значение 30. Потому что ширина не может выражаться отрицательным числом.

Итак, через x была обозначена ширина участка. Она равна тридцати метрам. А длина была обозначена через выражение x + 10. Подставим в него найденное значение x и вычислим длину:

x + 10 = 30 + 10 = 40 м

Значит длина участка составляет сорок метров, а ширина тридцать метров. Эти значения удовлетворяют условию задачи, поскольку если перемножить длину и ширину (числа 40 и 30) получится 1200 м2

40 × 30 = 1200 м2

Теперь ответим на вопрос задачи. Какова длина изгороди? Чтобы её вычислить нужно участка.

Периметр прямоугольника это сумма всех его сторон. Тогда:

P = 2(a + b) = 2 × (40 + 30) = 2 × 70 = 140 м.

Ответ: длина изгороди огородного участка составляет 140 м.

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

• Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3.
• А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
• Чуть сложнее работать со степенью, имеющей рациональный  и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
• В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Вычислите значение степенного выражения 23·(42−12).

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.

Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.

Ответ: 23·(42−12)=32.

Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.

История изучения квадрата

Древний мир воспринимает квадрат, главным образом, как четыре стороны света. Вообще, несмотря на множество четырехугольников, именно у квадрата главное число — четыре. Для ассирийцев и перуанцев квадрат — весь мир, то есть он представляет четыре основных направления, стороны света.

Даже Вселенную представляли как квадрат, еще и разделенный на четыре части — это видение жителей Северной Америки. Для кельтов вселенная — это целых три квадрата, вложенных друг в друга, а из центра вытекают четыре (!) реки. А египтяне вообще обожествляли эту фигуру!

Впервые описали квадрат посредством математических формул греки. Но для них этот многоугольник обладал только отрицательными характеристиками. Пифагор вообще не любил четные числа, видя в них слабость и женственность.

Даже в религиях присутствует квадрат. В Исламе Кааба — пуп Земли — имеет не какую-нибудь сферическую, а именно кубическую форму.

В Индии главной графемой, изображающей Землю, или символом земли, был перекрещенный квадрат. И снова речь идет о четырех сторонах света, четырех областях земли.

В Китае квадрат — это мир, гармония и порядок. Хаос побеждается построением квадратной Вары. А квадрат, вписанный в круг, является основой видения мира, символизируя единство и связь Космоса и Земли.