Как нарисовать ровный эллипс. как рисовать овалы

Фокусы, эксценриситет и директрисы эллипса.

У эллипса есть две замечательные точки, которые называются его фокусами.

Определение.

Пусть по определению
$$
c^{2}=a^{2}-b^{2}\label{ref2}
$$
и \(c \geq 0\).

Фокусами называются точки \(F_{1}\) и \(F_{2}\) с координатами \((c, 0)\) и \((-c, 0)\) в канонической системе координат (рис. 8.3).

Рис. 8.3. Фокусы эллипса.

Для окружности \(c=0\), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.

Определение.

Отношение
$$
\varepsilon=\frac{c}{a}\label{ref3}
$$
называется эксцентриситетом эллипса.

Отметим, что \(\varepsilon < 1\).

Утверждение 2.

Расстояние от произвольной точки \(M(x, y)\), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы \(x\):
$$
r_{1}=|F_{1}M|=a-\varepsilon x,\ r_{2}=|F_{2}M|=a+\varepsilon x.\label{ref4}
$$

Очевидно, что \(r_{1}^{2}=(x-c)^{2}+y^{2}\). Подставим сюда выражение для \(y^{2}\), найденное из уравнения эллипса. Мы получим
$$
r_{1}^{2}=x^{2}-2cx+c^{2}+b^{2}-\frac{b^{2}x^{2}}{a^{2}}.\nonumber
$$

Учитывая равенство \eqref{ref2}, это можно преобразовать к виду
$$
r_{1}^{2}=a^{2}-2cx+\frac{c^{2}x^{2}}{a^{2}}=(a-\varepsilon x)^{2}.\nonumber
$$
Так как \(x \leq a\) и \(\varepsilon < 1\), отсюда следует, что справедливо первое из равенств \eqref{ref4}: \(r_{1}=a-\varepsilon x\). Второе равенство доказывается аналогично.

Утверждение 3.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса \(2a\).

Необходимость. Если мы сложим равенства \eqref{ref4} почленно, то увидим, что
$$
r_{1}+r_{2}=2a.\label{ref5}
$$Достаточность. Пусть для точки \(M(x, y)\) выполнено условие \eqref{ref5}, то есть
$$
\sqrt{(x-c)^{2}+y^{2}}=2a-\sqrt{(x+c)^{2}+y^{2}}.\nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^{2}=a\sqrt{(x+c)^{2}+y^{2}}.\label{ref6}
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение \eqref{ref2}. Мы придем к \(b^{2}x^{2}+a^{2}y^{2}=a^{2}b^{2}\), равносильному уравнению эллипса \eqref{ref1}.

С эллипсом связаны две замечательные прямые, называемые его директрисами. Их уравнения в канонической системе координат (рис. 8.4)
$$
x=\frac{a}{\varepsilon},\\ x=-\frac{a}{\varepsilon}.\label{ref7}
$$
Директрису и фокус, которые лежат по одну сторону от центра, будем считать соответствующими друг другу.

Рис. 8.4. Фокусы и директрисы эллипса.

Утверждение 4.

Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса \(\varepsilon\).

Докажем это предложение для фокуса \(F_{2}(-c, 0)\). Пусть \(M(x, y)\) — произвольная точка эллипса. Расстояние от \(M\) до директрисы с уравнением \(x=-a/\varepsilon\) по формуле (9) §3 гл. II равно
$$
d_{2}=|x+\frac{a}{\varepsilon}|=\frac{1}{\varepsilon}(\varepsilon x+a).\nonumber
$$
Из формулы \eqref{ref4} мы видим теперь, что \(r_{2}/d_{2}=\varepsilon\).

Обратно, пусть для какой-то точки плоскости \(r_{2}/d_{2}=\varepsilon\), то есть
$$
\sqrt{(x+c)^{2}+y^{2}}=\varepsilon \left(x+\frac{a}{\varepsilon}\right).\nonumber
$$
Так как \(\varepsilon=c/a\), это равенство легко приводится к виду \eqref{ref6}, из которого, как мы знаем, следует уравнение эллипса.

Построение эллипсов в AutoCAD по центральной точке и двум полуосям

Вызываем команду Автокад Эллипс, затем выбираем опцию Центр. В командной строке появится запрос:

Центр эллипса:

Укажем точку центра эллипса в Автокад щелчком мыши на чертеже. Появится штриховая линия желтого цвета, которая будет следовать от центральной точки эллипса до курсора-перекрестия. Программа выдаст запрос:

Конечная точка оси:

Можете указать конечную точку оси эллипса щелчком мыши на чертеже или ввести половинное значение длины оси в командную строку. Появится предварительный вид эллипса Автокад, который будет изменяться вместе с перемещением курсора. Штриховая линия будет следовать от средней точки указанной оси (от центра эллипса) до курсора-перекрестия. Программа отобразит следующий запрос:

Длина другой оси или :

В ответ на который вы можете указать точку на чертеже или ввести половинное значение оси в командную строку. Как только вы укажете длину второй оси, эллипс в Автокаде будет построен, а команда «Эллипс» прекратить выполнение.

10.8. Эллипс и его свойства window.top.document.title = «10.8. Эллипс и его свойства»;

В § 7 было получено уравнение фигуры, которую мы назвали эллипсом:

В соответствии с формулами преобразования координат выразим старые координаты через новые по формулам:

канонической

k < 1a > b > 0x’ (y’)x (y)

каноническим уравнением эллипса

Рассмотрим свойства эллипса.

Свойство 10.1. 

Эллипс пересекает каждую из осей координат в двух точках.

Точки A, B, C и D называются вершинами эллипса. Отрезок AC называется большой осью эллипса, отрезок BD – малой осью. Числа a и b называют полуосями эллипса. Точки  и  где  называются фокусами эллипса.

Пусть M (x; y) – произвольная точка эллипса. Найдем расстояния от точки M до фокусов эллипса.

(x; y)M

Величину  называют эксцентриситетом эллипса. Очевидно, для эллипса ε < 1. Поскольку  то отсюда следует, что a – εx > 0. Поэтому  

Свойство 10.2. 

Сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равная удвоенной большей полуоси.

Свойство 10.3. 

Эллипс имеет две взаимно перпендикулярные оси симметрии.

Свойство 10.4. 
Эллипс имеет центр симметрии.

Центр симметрии эллипса называется центром эллипса.

Свойство 10.5. 
Эллипс может быть получен сжатием окружности.

В качестве характеристики формы эллипса удобнее пользоваться эксцентриситетом. Так как

При малых значениях эксцентриситета эллипс мало отличается от окружности. При ε = 0 эллипс превращается в окружность.

В § 7 мы определили эллипс как множество точек, отношение расстояний от которых до данной точки A и данной прямой l есть величина постоянная и равная числу k.

Рассмотрим, какие координаты имеет точка A и какое уравнение – прямая l в канонической системе координат. Для начала отметим, что в силу введенных ранее обозначений

Al

Координаты точки  при переходе в новую систему будут равны:

A

Уравнение прямой в исходной системе координат имело вид  После замены системы координат получим новое уравнение прямой l

ε < 1

Прямая x = –d называется директрисой, соответствующей фокусу F₁(-c; 0). Наряду с этой директрисой вводят прямую x = d, которая является директрисой, соответствующей фокусу F₂(c; 0).

С учетом свойств симметрии эллипса, свойство, с помощью которого мы определили эллипс, в новых терминах можно сформулировать следующим образом: отношение расстояния от любой точки эллипса до одного из его фокусов к расстоянию от этой точки до соответствующей ему директрисы есть величина постоянная и равная эксцентриситету. Вид эллипса в канонической системе координат и его директрисы приведены на рис. 10.8.1.

Рисунок 10.8.1

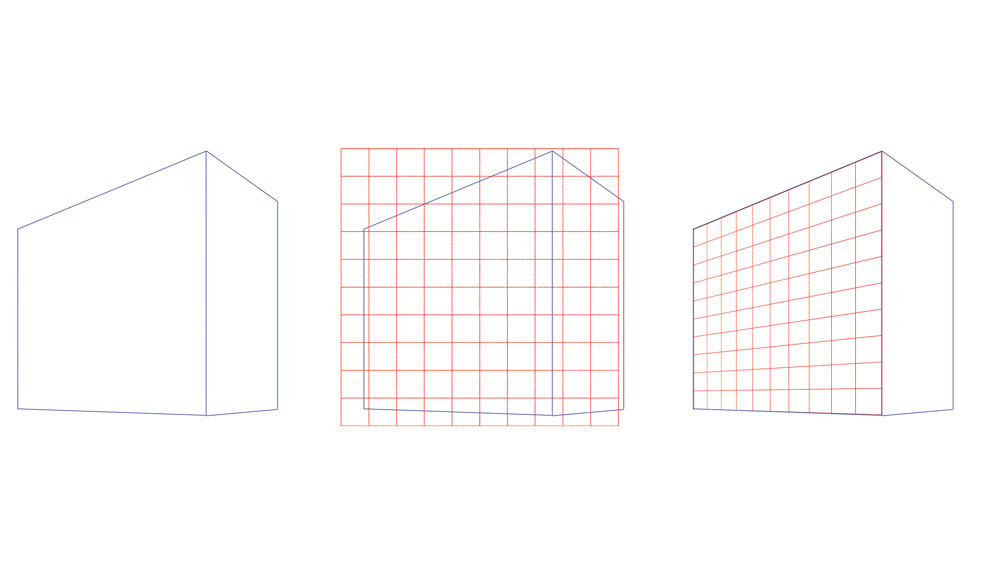
Элементы черчения для начинающих — построение эллипса техническими способами.

Первый способ начертить эллипс.

Давайте начертим эллипс, вписанный в прямоугольник А.

Сначала при помощи циркуля найдите, где круг (показанный на рисунке А)
пересекает длинную среднюю линию. Эти пересечения обозначены точками (1) и (2).

Рис. 13.5.

Воткните в эти точки булавки, а третью булавку (3) — в конце средней линии.

Крепко обвяжите эти булавки прочной льняной ниткой, как показано на рисунке
В.

Удалите булавку (3) и очертите карандашом эллипс, как показано на рисунке С. Нитка должна быть постоянно равномерно
натянута.

Второй способ построения.

Вот еще один способ как начертить эллипс, вписанный в прямоугольник А.

Рис. 13.6.

Начертите два круга с центром в точке О. Диаметр одного круга должен быть
равен ширине прямоугольника, а диаметр другого — длине прямоугольника, как
показано на рисунке D.

Теперь проведите линии наподобие спиц колеса, как показано на рисунке Е.

Через точки пересечения спиц с малым кругом проведите линии, параллельные
длинным сторонам. Через точки пересечения спиц с большим кругом проведите
линии, параллельные коротким сторонам.

Рис. 13.7.

Эллипс проходит через точки пересечения линий, параллельных коротким
сторонам и параллельных длинным сторонам, как показано на рисунке F.

Третий способ построения эллипса.

Приводим еще один способ начертить эллипс определенной величины.

Возьмите полоску бумаги и отметьте на ней половину длины данного в качестве
основы прямоугольника. Обозначьте точку буквой L, как показано на рисунке G.

Рис. 13.8.

Далее положите полоску вдоль линии ширины и буквой W обозначьте точку,
отмечающую половину этой ширины, как показано на рисунке Н.

Теперь поместите бумажную полоску так, чтобы точка L касалась линии ширины,
а точка W касалась линии длины, как показано на рисунке I.

Кончик полоски (обозначенный буквой Е) показывает, где проходит контур
эллипса.

Продолжайте двигать полоску по кругу, пока не отметите столько точек,
сколько вам нужно.

Этот метод подходит для вычерчивания эллипсов любой величины. При черчении
после обозначения точек можно вычертить контур эллипса по лекалу.

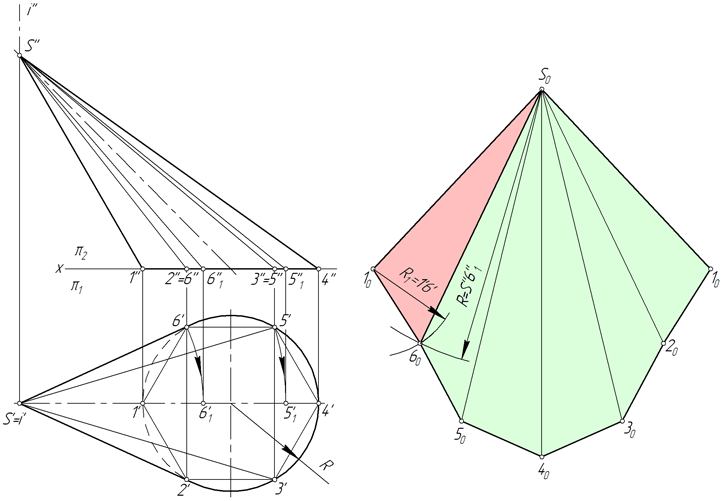
Построение лекальных кривых ,парабола

Рисунок 43. Пересечение конуса плоскостью по параболе. Построение параболы по фокусу и директрисе.

Если рассечь наклонной плоскостью Р круговой конус,параллельной одной из его образующих,то в плоскости сечения образуется парабола.(смотри рисунок 43 а).Парабола это незамкнутая плоская кривая линия. Каждая точка параболы расположена от данной прямой -MN,и от фокуса -F на одинаковом расстоянии.

Прямая MN является направляющей и расположена перпендикулярно оси параболы.Между направляющей -MN и фокусом -F, прямо посередине расположена вершина параболы А. Для того чтобы построить параболу по фокусу и заданной направляющей,через точку фокуса-F , проведем ось параболы -Х,  перпендикулярно направляющей -MN.

Разделим пополам отрезок-EF и получим вершину параболы-А.От вершины параболы на произвольном расстоянии проведем прямые перпендикулярно оси параболы. Из точки -F радиусом который равен расстоянию-L, от соответствующей прямой до направляющей, например СВ, делаем на это прямой засечки. В данном случае точки С и В.

Таким образом построив несколько пар симметричных точек,проведем с помощью лекала через них плавную кривую. На рисунке( 43 в) приводится пример построения параболы касательной к двум прямым ОА и ОВ в точках А и В. Отрезки ОА и ОВ делят на одинаковое число  равных частей(например делят на восемь). После этого нумеруются полученные точки деления и соединяются прямыми 1-1; 2-2; 3-3 (смотри рисунок 43, в) и так далее. Эти прямые к параболической кривой являются касательными. В образованный прямыми контур далее вписывают плавную касательную  кривую-параболу.

Построение гиперболы

Если рассечь прямой и обратный конусы плоскостью, параллельной двум его образующим или в частном случае параллельно оси, то в плоскости сечения получится гипербола, состоящая из двух симметричных ветвей (смотри рисунок 45, а).

Рисунок 45. Пересечение конуса плоскостью по гиперболе (а) и построение гиперболы (б).

Гиперболой (рисунок 45,б) называют плоскую кривую у которой разность расстояний от каждой ее точки до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная и равная расстоянию между ее вершинами a и b, например SF1-SF2=ab. У гиперболы две оси симметрии -действительная  АВ и мнимая CD.

Две прямые KL и K1 L1, проходящие через центр О гиперболы и касающиеся ее ветвей в бесконечности, называются асимптотами. Гиперболу можно построить по заданным вершинам a и b и фокусам F1 и F2. Вершины гиперболы определяем, вписывая прямоугольник в окружность построенном на фокусном расстоянии (отрезке F1 и F2), как на диаметре.

На действительной оси АВ справа от фокуса F2 намечаем произвольные 1, 2, 3, 4, … Из фокусов F1 и F2 проводим дуги окружностей сначала радиусом а-1, затем b-1 до взаимного пересечения по обе стороны от действительной оси гиперболы. Далее выполним взаимное пересечение следующей пары дуг радиусами а-2 и b-2( точка S) и так далее.

Полученные точки пересечения дуг принадлежат правой ветви гиперболы. Точки левой ветви будут симметричны построенным точкам относительно мнимой оси CD.

Синусоида

Синусоидой называется проекция траектории точки,движущейся по цилиндрической винтовой линии, на плоскость, параллельную оси цилиндра. Движение точки складывается из равномерно -вращательного движения (вокруг оси цилиндра) и равномерно-поступательного ( параллельно от цилиндра).

Рисунок 46. Построение синусоиды

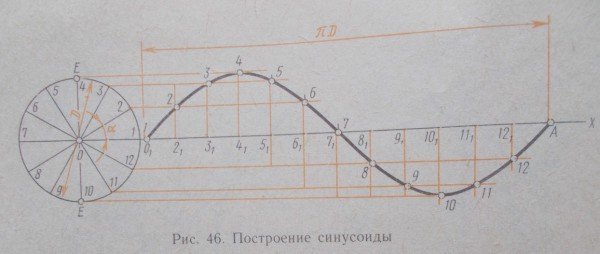Синусоида представляет собой плоская кривая, которая показывает изменение тригонометрической функции синуса в зависимости от изменения величины угла. для построения синусоиды ( рисунок 46) через центр О окружности диаметра D проведем прямую ОХ и на ней отложим отрезок О1 А, равный длине окружности π D. Этот отрезок и окружность делим на одинаковое число равных частей. Из полученных и занумерованных точек проведем взаимно перпендикулярные прямые. Полученные точки пересечения этих прямых соединим с помощью лекала плавной кривой.

Вычерчивание лекальных кривых

Лекальные кривые строят по точкам. Соединяют эти точки с помощью лекал, предварительно от руки прорисовывая кривую по точкам. принцип соединения отдельных точек кривой заключается в следующем:

Выбираем ту часть дуги лекала, которая лучше всего совпадает с наибольшим количеством точек очерчиваемой кривой. Далее проведем не всю дугу кривой, совпадащую с лекалом, а лишь среднюю часть ее. После этого подберем другую часть лекала, но так, чтобы эта часть касалась примерно одной трети проведенной кривой и не менее двух последующих точек кривой , и так далее. Таким образом обеспечивается плавный переход между отдельными дугами кривой.

РЕКОМЕНДУЕМ выполнить перепост статьи в соцсетях!

Самый простой метод

Начнём с самого простого метода. Сразу оговорочка: этот метод годится только в случае, если окружность имеет радиус не больше длины нашего остроносого помощника. Суть метода в превращении кисти руки в циркуль:

1. Ставим точку на бумаге, обозначая центр будущей окружности;
2. Берём карандаш указательным и большим пальцами захватом сверху на расстоянии радиуса от кончика, чтобы остальная его часть упиралась в тыльную часть ладони, напротив большого пальца;
3. Ставим средний палец, плотно прижатый к указательному в намеченную точку. Постоянно следите, чтобы он не сдвигался с этой точки!
4. Упираем кончик остроноса в бумагу и начинаем плавно вращать бумагу свободной рукой до полного круга.
5. Обводим намеченные контуры до нужной кондиции.

Метод очень простой. Если не получается проводить цельную линию или нет возможности вращать бумагу. Можно делать небольшие засечки, потом их соединить. Вращаться же можно самому вокруг листа – результат будет тот же.

Способы рисования овала на перекрытии

Способ#1

• вкручиваем саморез/вбиваем гвоздь в потолок — это и будет центром первого круга,
• приматываем к саморезу/гвоздю проволоку/веревку,
• приматываем к другому концу карандаш/маркер,
• теперь определяем центр второго круга таким же образом, как и центр первого. Эти два круга должны пересекаться и образовывать овал при пересечении. Вот, как нарисовать овал на потолке. Если же вам нужна не овальная, а просто круглая форма, — то рисовать второй круг и вовсе не потребуется.

Естественно, диаметр вы определяете произвольно, согласно своему дизайн-проекту.

Способ#2

Можно прибегнуть к использованию другого варианта: просто изготовить овальную форму, скажем, из плотного картона — и прикрепить ее к потолку (или обвести карандашом/маркером).

Вот, какой будет последовательность действий, если вы решили прибегнуть к использованию данного варианта:

• берем материал (картон/ДВП/фанеру) — и рисуем овал таким же образом, как мы рисовали его на потолке в «Способе#1»,
• теперь, как сказал бы Микеланджело, — отсекаем все лишнее, то есть, оставляем только то, что нам нужно — овальную форму,
• прикрепляем получившейся овал к поверхности потолка. Сделать это можно при помощи саморезов/клея/можно и воспользоваться другим способом (но надежнее все-таки саморезы),
• монтируем несущий профиль для будущего гипсокартонного потолка.

И да, о том, как выполнять последующую работу по монтаже каркаса и так далее, — мы поговорим чуть позже, — когда рассмотрим все способы изготовления овальной формы.

Способ#3

Не самое простое решение, но, все же, для пущей солидности, следует уделить внимание и этому способу. Предстоит составить чертеж

Для этого берем миллиметровую бумагу и перерисовываем наш потолок в масштабе, скажем, 1:1 (1 м = 1 см).

Теперь нужно отметить контрольные точки. При этом исходить нужно из того, что в центре потолка будет располагаться центр овала. Теперь переводим сантиметры в метры и записываем результат. Теперь нужно разметить рабочую поверхность, используя рулетку и линейку, руководствуясь полученными данными.

Способ#4

Данный способ подойдет вам, если вы умеете хорошо рисовать/чертить в больших масштабах. Вы можете сразу начертить нужную овальную форму на перекрытии с использованием карандаша и измерительных приборов.

Таким образом вы облегчите задачу, но, при этом, возможны неточности. Это не критично, так как, даже если овал не будет идеальным, — в процессе обшивки гипсокартоном, изъяны будет несложно устранить.

Способ#5

• в центре будущего овала намечаем точку,
• создаем некое подобие розы ветров: от намеченной точки чертим отрезки одинаковой длины. Они должны быть направлены в четыре стороны,
• чертим окружность из этих точек при помощи карандаша и проволоки/веревки — и вот, мы получаем то, что нам нужно.

Способ#6

• выбираем две точки, располагающиеся на центральной линии помещения (это в том случае, — если овал будет располагаться по центру),
• измеряем расстояние между двумя точками. Это расстояние — и есть диаметр будущей окружности, которая и будет выполнять роль границы овала. Если такое объяснение не совсем понятное (а оно — совсем не понятное), — к вашим услугам конкретный пример: образовался у вас отрезок, скажем, 0,5 см длиной. Поскольку это — диаметр целой окружности, — нам нужно разделить его на две равные части. Тогда у вас будет тот размер, что нужно очертить.

Способ#7

Этот метод нельзя назвать простым. Но, при этом, он дает наибольшую точность. Рассмотрим его поэтапно:

• чертим оси координат,
• обводим маркером/карандашом ромб (размер не принципиально важен, главное, — чтобы этот ромб был равносторонним),
• рисуем дуги в противоположных углах, — их размер должен равняться длине перпендикулярных прямых линий, которые опущены в эти углы.

«Способ#7» особенно хорош, если за короткое время нужно сделать дугообразный потолок. Даже если в школе у вас была, скажем, не самая высокая оценка по черчению, — вы справитесь, потому что здесь и не требуется быть искушенным в данной учебной дисциплине: профессиональные навыки тут не нужны.

Другие свойства

• Оптические
  • Свет от источника, находящегося в одном из фокусов, отражается эллипсом так, что отраженные лучи пересекутся во втором фокусе.
  • Свет от источника, находящегося вне любого из фокусов, отражается эллипсом так, что отраженные лучи ни в каком фокусе не пересекутся.
• Если F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F1X){\displaystyle (F_{1}X)} равен углу между этой касательной и прямой (F2X){\displaystyle (F_{2}X)}.
• Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
• Эволютой эллипса является астроида, вытянутая вдоль вертикальной оси.
• Точки пересечения эллипса с осями являются его вершинами.
• Эксцентриситет эллипса, то есть отношение e=ca=1−b2a2(⩽e<1),{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1),}

  Если эксцентриситет эллипса равен нулю (что то же самое, что фокальное расстояние равно нулю: F1F2=0{\displaystyle F_{1}F_{2}=0}), то эллипс вырождается в окружность.

  характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.

• Экстремальные свойства

  Если F{\displaystyle F} — выпуклая фигура и Tn{\displaystyle T_{n}} — вписанный в F{\displaystyle F} n{\displaystyle n}-угольник максимальной площади, то
  S(Tn)≥S(F)⋅nsin⁡(2⋅π/n)2⋅π,{\displaystyle S(T_{n})\geq S(F)\cdot {\frac {n}{\sin(2\cdot \pi /n)}}{2\cdot \pi },}

где S(F){\displaystyle S(F)} обозначает площадь фигуры F{\displaystyle F}

Более того в равенство достигается в том и только в том случае, если F{\displaystyle F} ограничено эллипсом.

.

Среди всех выпуклых замкнутых кривых, ограничивающих данную площадь, эллипс имеет максимальную аффинную длину.

Если произвольный эллипс вписан в треугольник ABC и имеет фокусы P и Q, тогда для него справедливо соотношение

PA¯⋅QA¯CA¯⋅AB¯+PB¯⋅QB¯AB¯⋅BC¯+PC¯⋅QC¯BC¯⋅CA¯=1.{\displaystyle {\frac {{\overline {PA}}\cdot {\overline {QA}}}{{\overline {CA}}\cdot {\overline {AB}}}}+{\frac {{\overline {PB}}\cdot {\overline {QB}}}{{\overline {AB}}\cdot {\overline {BC}}}}+{\frac {{\overline {PC}}\cdot {\overline {QC}}}{{\overline {BC}}\cdot {\overline {CA}}}}=1.}

Если лестницу (бесконечно тонкий отрезок прямой) прислонить к вертикальной стенке с горизонтальным полом, и один конец лестницы будет скользить по стенке (всё время касаясь её) а второй конец лестницы будет скользить по полу (всё время касаясь его), тогда любая фиксированная точка лестницы (не на её концах), будет двигаться по дуге некоторого эллипса. Это свойство остаётся верным, если мы возьмём точку не внутри лестницы-отрезка, а на её мыслимом продолжении. Последнее свойство используется в описанном выше.mw-parser-output .ts-Переход img{margin-left:.285714em} эллипсографе.

Касательная, проходящая через точку (x0,y0){\displaystyle (x_{0},y_{0})}, принадлежащую эллипсу, имеет следующее уравнение:

xxa2+yyb2=1.{\displaystyle {\frac {xx_{0}}{a^{2}}}+{\frac {yy_{0}}{b^{2}}}=1.}

Команда AutoCAD Эллипс (Ellipse)

За создание эллипса в Автокад отвечает команда Эллипс/Ellipse, вызвать которую можно следующими способами (начать его построение): 

• построить эллипсы в Автокаде можно из строки меню пункт Рисование — строка Ellipse;
• создать его можно из вкладки Главная ленты инструментов — в группе инструментов Рисование кнопка «Центр, (Ось, конец)», т.е. вам сразу в ленте доступны опции команды Эллипс в Автокаде;
• нарисовать объект Эллипс можно из классической панели инструментов Рисование кнопка Ellipse;
• а так же непосредственное создание эллипса в программе из командной строки, прописав наименование команды в командной строке Эллипс/Ellipse.

С помощью циркуля[править]

1. Раствором циркуля, равным a, с центром в точке O отметим на одной из прямых точки P₁ и Р₂, а на второй прямой раствором, равным b — точки Q₁ и Q₂. Полученные точки являются вершинами эллипса, а отрезки P₁Р₂ и Q₁Q₂ — его большая и малая оси, соответственно.
2. Раствором циркуля, равным a, с центром в точке Q₁ (или Q₂) отметим на отрезке P₁Р₂ точки F₁ и F₂. Полученные точки являются фокусами эллипса.
3. На отрезке P₁Р₂ выберем произвольную точку T. Затем с помощью циркуля начертим две окружности: первую — радиуса, равным длине отрезка TP₁, с центром в точке F₁ и вторую радуса, равным длине отрезка TP₂, с центром в точке F₂. Точки пересечения этих окружностей принадлежат искомому эллипсу, так как сумма расстояний из обоих фокусов равна длине большой оси 2a.
4. Повторяя необходимое число раз шаги предыдущего пункта, получим искомый эллипс.

С помощью двух иголок и нитки[править]

В 2-х чёрных фокусах — 2 иголки, соединённые нитью. В красной точке — карандаш, который натягивает нить

Примем, что

• AA₁ = 2a — это большая ось эллипса,
• BB₁ = 2b — это малая ось эллипса,
• Точки F и F₁ — фокусы эллипса. Фокусы лежат на прямой AA₁ на расстоянии a от точки B. Расстояние между фокусами FF₁ равно 2a2−b2{\displaystyle 2{\sqrt {a^{2}-b^{2}}}}

Этот способ основан на определении (фокальном свойстве) эллипса:
эллипс — геометрическое место точек, сумма расстояний от каждой из которых до фокусов постоянна и равна 2a.

Для этого способа лист бумаги нужно приколоть к чертёжной доске.

1. В точки фокусов эллипса F и F₁ втыкаются две иголки (иглы́, булавки, кнопки, тонких гво́здика…)

2. К этим двум иголкам привязываются (у са́мой поверхности бумаги) концы нити длиной 2a — нужно, чтобы между иголками F и F₁ было 2a длины нити. Это удобно осуществить так:

1. Берётся нитка длиной в несколько раз больше 2a.
2. Один из концов нити привязывается к иголке F.
3. В точку B втыкается третья иголка.
4. Нить кладётся на лист дальше иголки B от прямой FF₁, один раз (один виток) оборачивается вокруг иголки F₁ (так что может скользить по ней), затем, держа нить левой рукой за свободный конец, её натягивают вдоль ломанной FBF₁.
5. Свободный конец нити зажимается в кулаке левой руки, и кулак прижимают к листу бумаги в стороне от будущего эллипса — так, чтобы кулак (и нить) не перемещались ни в направлении к точке F₁ ни в направлении прочь от неё. Кулак держать так (зафиксированным) до тех пор, пока эллипс не будет построен. Вместо удерживания конца нити рукой, можно привязать конец нити к четвёртой иголке или кнопке, и, натянув нить, воткнуть эту иголку/кнопку в стороне от будущего эллипса.
6. Выдёргиваем (удаляем) иголку B (нить при этом утрачивает натяжение).

Примечание: Вместо точки B третью иголку можно было воткнуть в точку A.

3. Грифелем карандаша оттягиваем участок нити между иголками F и F₁ в сторону от прямой AA₁, натягивая нить.

4. Оттягивающий нить грифель карандаша прижимаем к бумаге и, скользя грифелем по натянутой нити от точки A до точки A₁, рисуем половину эллипса, лежащую по одну сторону от прямой AA₁.

5. Располагаем грифель карандаша по другую сторону от нити, оттягиваем нить в другую сторону от прямой AA₁ и, так же как первую, рисуем вторую половину эллипса.

Чтобы нить не спадала вниз с грифеля карандаша, на лист бумаги под нить можно подложить (шайбу подходящей толщины) и оттягивающим нить грифелем касаться бумаги внутри отверстия шайбы — чтобы во время рисования эллипса натянутая нить лежала на шайбе (грифель будет перемещать шайбу по бумаге и вдоль нити).

Усовершенствование способаправить

Можно не привязывать нить ни к одной из иголок и нарисовать эллипс одним движением карандаша, а не двумя:

1. Так же втыкаем три иголки — в точки F, F₁ и B.
2. Треугольник FF₁B окружаем и обтягиваем нитью, и связываем концы натянутой нити — получается кольцо из нити. Длина кольца равна периметру треугольника FF₁B.
3. Выдёргиваем (удаляем) иголку B (кольцо из нити при этом утрачивает натяжение).
4. Поместив грифель карандаша внутри кольца из нити, оттягиваем грифелем нить в сторону от прямой FF₁, натягивая нить. Затем, удерживая нить натянутой, прижимаем грифель к бумаге и, скользя грифелем по натянутой нити вокруг отрезка FF₁, рисуем эллипс не двумя движениями руки с карандашом, а одним (круговым).

Примечание: Опять-таки, вместо точки B третью иголку можно было воткнуть в точку A.

Соотношения между элементами эллипса

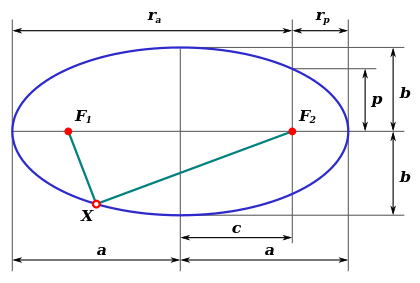
Части эллипса (описание см. в разделе «Связанные определения»)

• a{\displaystyle {\boldsymbol {a}}} — большая полуось;
• b{\displaystyle {\boldsymbol {b}}} — малая полуось;
• c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние (полурасстояние между фокусами);
• p{\displaystyle {\boldsymbol {p}}} — фокальный параметр;
• rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние (минимальное расстояние от фокуса до точки на эллипсе);
• ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние (максимальное расстояние от фокуса до точки на эллипсе);

a2=b2+c2{\displaystyle a^{2}=b^{2}+c^{2}}

e=ca=1−b2a2(⩽e<1).{\displaystyle e={\frac {c}{a}}={\sqrt {1-{\frac {b^{2}}{a^{2}}}}}\;\;\;(0\leqslant e<1).}.

p=b2a{\displaystyle p={\frac {b^{2}}{a}}}

	a{\displaystyle {\boldsymbol {a}}}	b{\displaystyle {\boldsymbol {b}}}	c{\displaystyle {\boldsymbol {c}}}	p{\displaystyle {\boldsymbol {p}}}	rp{\displaystyle {\boldsymbol {r_{p}}}}	ra{\displaystyle {\boldsymbol {r_{a}}}}
a{\displaystyle {\boldsymbol {a}}} — большая полуось	a{\displaystyle {\boldsymbol {a}}}	a=b1−e2{\displaystyle a={\frac {b}{\sqrt {1-e^{2}}}}}	a=ce{\displaystyle a={\frac {c}{e}}}	a=p1−e2{\displaystyle a={\frac {p}{1-e^{2}}}}	a=rp1−e{\displaystyle a={\frac {r_{p}}{1-e}}}	a=ra1+e{\displaystyle a={\frac {r_{a}}{1+e}}}
b{\displaystyle {\boldsymbol {b}}} — малая полуось	b=a1−e2{\displaystyle b=a{\sqrt {1-e^{2}}}}	b{\displaystyle {\boldsymbol {b}}}	b=c 1−e2e{\displaystyle b={\frac {c~{\sqrt {1-e^{2}}}}{e}}}	b=p1−e2{\displaystyle b={\frac {p}{\sqrt {1-e^{2}}}}}	b=rp1+e1−e{\displaystyle b=r_{p}{\sqrt {\frac {1+e}{1-e}}}}	b=ra1−e1+e{\displaystyle b=r_{a}{\sqrt {\frac {1-e}{1+e}}}}
c{\displaystyle {\boldsymbol {c}}} — фокальное расстояние	c=ae{\displaystyle c=ae}	c=be1−e2{\displaystyle c={\frac {be}{\sqrt {1-e^{2}}}}}	c{\displaystyle {\boldsymbol {c}}}	c=pe1−e2{\displaystyle c={\frac {pe}{1-e^{2}}}}	c=rpe1−e{\displaystyle c={\frac {r_{p}e}{1-e}}}	c=rae1+e{\displaystyle c={\frac {r_{a}e}{1+e}}}
p{\displaystyle {\boldsymbol {p}}} — фокальный параметр	p=a(1−e2){\displaystyle p=a(1-e^{2})}	p=b 1−e2{\displaystyle p=b~{\sqrt {1-e^{2}}}}	p=c 1−e2e{\displaystyle p=c~{\frac {1-e^{2}}{e}}}	p{\displaystyle {\boldsymbol {p}}}	p=rp(1+e){\displaystyle p=r_{p}(1+e)}	p=ra(1−e){\displaystyle p=r_{a}(1-e)}
rp{\displaystyle {\boldsymbol {r}}_{p}} — перифокусное расстояние	rp=a(1−e){\displaystyle r_{p}=a(1-e)}	rp=b 1−e1+e{\displaystyle r_{p}=b~{\sqrt {\frac {1-e}{1+e}}}}	rp=c 1−ee{\displaystyle r_{p}=c~{\frac {1-e}{e}}}	rp=p1+e{\displaystyle r_{p}={\frac {p}{1+e}}}	rp{\displaystyle {\boldsymbol {r}}_{p}}	rp=ra1−e1+e{\displaystyle r_{p}=r_{a}{\frac {1-e}{1+e}}}
ra{\displaystyle {\boldsymbol {r}}_{a}} — апофокусное расстояние	ra=a(1+e){\displaystyle r_{a}=a(1+e)}	ra=b 1+e1−e{\displaystyle r_{a}=b~{\sqrt {\frac {1+e}{1-e}}}}	ra=c 1+ee{\displaystyle r_{a}=c~{\frac {1+e}{e}}}	ra=p1−e{\displaystyle r_{a}={\frac {p}{1-e}}}	ra=rp 1+e1−e{\displaystyle r_{a}=r_{p}~{\frac {1+e}{1-e}}}	ra{\displaystyle {\boldsymbol {r}}_{a}}

Различные формы потолка

Помимо овальных и круглых форм из гипсокартона можно сделать любые волнообразные фигуры, все полностью зависит от вашей фантазии и воображения.

К примеру, популярными в последнее время стали фигурки в виде сердца, которые монтируются в спальню для влюбленных.

Интересным вариантом считается и двухуровневый потолок, основание которого выполняется в прямой форме, а вот второй уровень напоминает какую-либо фигуру.

Закругленные потолочные конструкции интересно смотрятся в гостиных и детских, где в гипсокартон устанавливаются светильники для дополнительной подсветки комнаты.

Все готово к отделке

Построение дуги окружности. Дуга по двум точкам, дуга по двум точкам и углу раствора.

Дуга по двум точкам.

Для того, чтобы построить дугу с указанием двух точек, вам нужно выбрать «Дуга по 2 точкам». В компактном меню либо же указать в меню сверху следующие команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам».

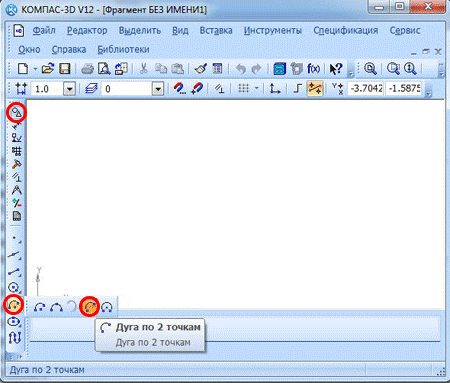
Для начала в нужном поле в свойственной панели от вас требуется ввести значение радиуса либо диаметра (к примеру, радиус в 100 мм) и нажать кнопку ввода.

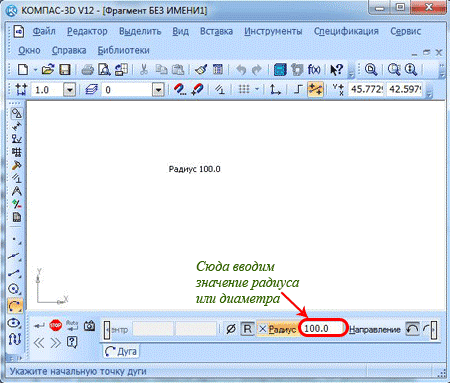
С помощью курсора или же в свойственной панели указываете координаты начала и конца дуги. Экран отобразит фантомные варианты построения.

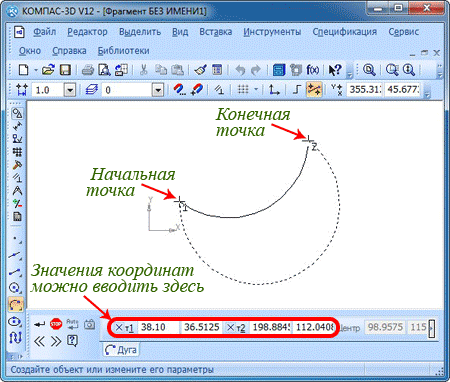
Вам нужно выбрать правильный и последовательно нажать пункты «Создать объект» и «Прервать команду».

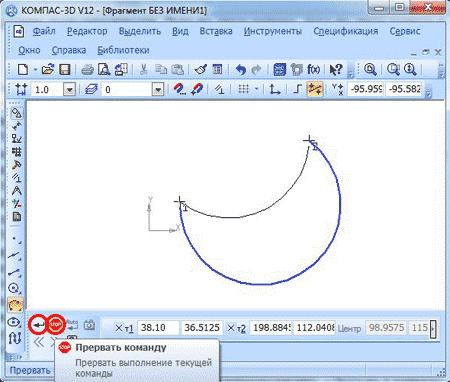
Если вы хотите построить дугу по диаметрально противоположным точкам, то радиус и диаметр программа рассчитает самостоятельно.

Дуга по двум точкам и углу раствора.

Для того, чтобы построить дугу с указанием двух точек и угла раствора, нужно нажать «Дуга по 2 точкам и углу раствора». В компактном меню или же в меню сверху выбрать команды «Инструменты» — «Геометрия» — «Дуги» — «Дуга по 2 точкам и углу раствора».

В свойственной панели для начала нужно ввести значение угла (к примеру, 220 градусов) и нажать клавишу ввода.

Потом вам нужно указать положение начала и конца дуги. Координаты могут указываться с помощью курсора либо введя их в нужные поля свойственной панели.

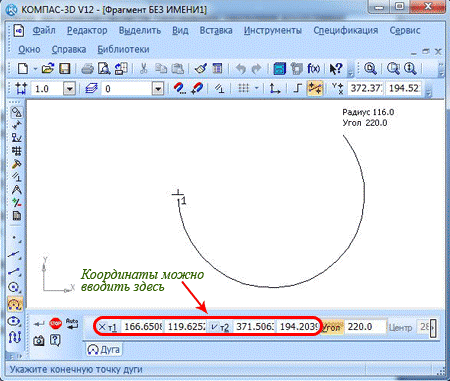
Прочие параметры, такие, как центральная точка и диаметр, программа определит самостоятельно. Построение завершается кнопками «Создать объект» и «Прервать команду».

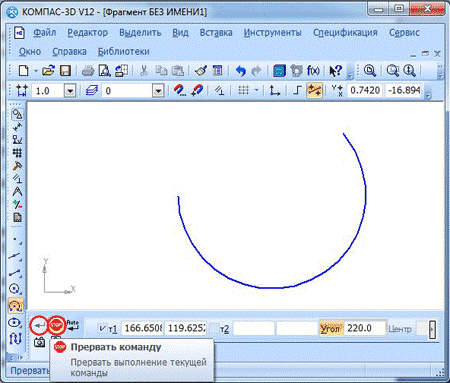
Нами были рассмотрены все возможности построения дуг в “Компас 3D”. Далее мы разберёмся, как строить эллипсы.