Законы математики

Примеры

1. Проверить коммутативность умножения матриц над полем вещественных чисел.

   Спойлер

   Пусть $ \small A \in \mathbb{M} _{m \times p} ,B \in \mathbb{M} _{p \times n}: $ $ \small C=A\times B;\ C \in \mathbb{M} _{m\times n} \Rightarrow $ $ \small c_{ij}= \underset{k=1} {\overset{p} {\sum}}a_{ik}b_{kj} .$ Очевидно, что для выполнения операции умножения, количество столбцов первой матрицы должно совпадать с количеством строк второй, следовательно, мы доказали, что коммутативность не выполняется для всех матриц, однако всё ещё может выполнятся для квадратных матриц. Проверим это: выполнение коммутативности для матриц будет выглядеть, как $ \small\forall \ A,B \in \mathbb{M}_{n} \ A\times B \overset{?}{=} B\times A,$ если рассматривать результирующую матрицу поэлементно, то это можно интерпретировать, как $ \small \underset{k=1} {\overset{m} {\sum }}a_{ik}b_{kj}\overset {?}{=} \underset{k=1}{ \overset{m}{\sum}}b_{ik}a_{kj},$ то есть в первой сумме мы перемножаем строку первой матрицы на столбец второй, а во второй строку второй матрицы на столбец первой. Ясно, что результаты таких действий будут равны тогда и только тогда, когда обе матрицы будут симметрическими (то есть будут совпадать с собой транспонированными $ \small A^{T}=A$). Следовательно, коммутативность не выполняется даже для квадратных матриц.

2. Доказать, что если ассоциативность выполняется для трёх элементов множества, то способ расстановки скобок не влияет на результат при любом количестве операндов, то есть если:
   $ \forall x,y,z \in \mathbb{P}: $ $ (x\circ y)\circ z=y\circ (x\circ z) ,$ то в выражении $ a _{1} \circ a _{2} \circ … \circ a _{n-1} \circ a _{n}, \,a_{i} \in \mathbb{P} i=\overline{1,n} $ результат не зависит от того, как мы расставим скобки.

   Спойлер

   Докажем это утверждение математической индукцией по количеству операндов.База индукции:
   Минимальное количество переменных равно трём, следовательно, из условия имеем: $ \small \forall \,a_{1}, a_{2}, a_{3} \in \mathbb{P}: $ $ \small ( a_{1}\circ a_{2})\circ a_{3}= a_{2}\circ (a_{1}\circ a_{3}) .$ База индукции доказана.Предположение индукции:
   $ \small \forall \,n \in \mathbb{N}: $результат выражения $ \small a _{1} \circ a _{2} \circ … \circ a _{n-1} \circ a _{n} \,$ не зависит от порядка расстановки скобок.Шаг индукции:
   Пусть предположение индукции справедливо для $ \small \forall \, n \in \mathbb{N} ,$ докажем, что тогда оно справедливо и для $ \small n+1 .$
   Пусть $ \small 1\leq p\leq m< n+1 .$ То есть можно задать справедливое разбиение: $ \small a _{1} \circ a _{2} \circ … \circ a _{n-1} \circ a _{n} = $ $ \small (a _{1} \circ a _{2} \circ … \circ a _{p-1} \circ a _{p}) \circ $ $ \small (a _{p+1} \circ … \circ a _{m-1} \circ a _{m})\circ $ $ \small (a _{m+1} \circ … \circ a _{n-1} \circ a _{n} \circ a _{n+1}) .$ Произведём замену:
   $ \small (a _{1} \circ a _{2} \circ … \circ a _{p-1} \circ a _{p}) = a $
   $ \small (a _{p+1} \circ … \circ a _{m-1} \circ a _{m}) = b $
   $ \small (a _{m+1} \circ … \circ a _{n} \circ a _{n+1}) = c $
   По базе индукции имеем $ \small (a \circ b) \circ c = a \circ (b \circ c ),$ то есть $ \small \circ $ $ \small (a _{m+1} \circ … $ $ \circ a _{n-1} \circ a _{n} \circ a _{n+1})=$ $ \small (a _{1} \circ a _{2} \circ … $ $ \circ a _{p-1} \circ a _{p}) \circ $ $ \small .$
   В силу свободы выбора $ \small p, m,$ и свободы количества замен такого рода теорема доказана.

3. Проверить дистрибутивность сложения матриц над полем вещественных чисел относительно умножения.

   Спойлер

   Пусть $ A \in \mathbb{M} _{m\times n}; B,C \in \mathbb{M} _{n\times m},$ докажем, что $ A\cdot (B+C)=A\cdot B+A\cdot C.$ Заметим, что $ A=\left \| a_{ij} \right \|,$ $ B=\left \| b_{ji} \right \|,$ $ C=\left \| c_{ji} \right \|,$ $ i=\overline{1,m},$ $ j =\overline{1,n}$, тогда $ A\cdot (B+C)=$ $ \ \left \| a_{ij} \right \|\cdot (\left \| b_{ji} \right \| + \left \| c_{ji} \right \|)=$ $ \ \left \| a_{ij} \right \|\cdot (\left \| b_{ji} + c_{ji} \right \|) = $ $ \ \left \| \underset{i=1}{ \overset{m}{\sum}} a_{ij} \cdot (b_{ji} + c_{ji})\right \| = $ $ \ \left \| \underset{i=1}{ \overset{m}{\sum}} a_{ij} \cdot b_{ji} + \underset{i=1}{ \overset{m}{\sum}} a_{ij} \cdot c_{ji}\right \|=$ $ \ \left \| \underset{i=1}{ \overset{m}{\sum}} a_{ij} \cdot b_{ji} \right \| + \left \| \underset{i=1}{ \overset{m}{\sum}} a_{ij} \cdot c_{ji}\right \| = $ $ \ A\cdot B+A\cdot C.$
   Правая дистрибутивность доказывается аналогично.

Неассоциативность

Операцию над двоичными числами на наборе S, который не удовлетворяет ассоциативный закон, называют неассоциативной. Символически,

Для такой операции действительно имеет значение заказ оценки. Например:

(5-3)-2 \, \ne \, 5-(3-2)

(4/2)/2 \, \ne \, 4 / (2/2)

2^ {(1^2)} \, \ne \, (2^1) ^2

Также обратите внимание на то, что бесконечные суммы не вообще ассоциативны, например:

(1-1) + (1-1) + (1-1) + (1-1) + (1-1) + (1-1) + \dots \, = \, 0

тогда как

1 + (-1+1) + (-1+1) + (-1+1) + (-1+1) + (-1+1) + (-1 +\dots \, = \, 1

Исследование неассоциативных структур является результатом причин, несколько отличающихся от господствующей тенденции классической алгебры. Одной областью в пределах неассоциативной алгебры, которая стала очень большой, является область алгебр Ли. Там ассоциативный закон заменен личностью Джакоби. Алгебры Ли резюмируют существенную природу бесконечно малых преобразований и стали повсеместными в математике.

Есть другие определенные типы неассоциативных структур, которые были изучены подробно. Они имеют тенденцию происходить из некоторых определенных заявлений. Некоторые из них возникают в комбинаторной математике. Другие примеры: квазигруппа, Квазиобласть, Неассоциативное кольцо.

Неассоциативность вычисления с плавающей запятой

В математике, дополнении и умножении действительных чисел ассоциативно. В отличие от этого, в информатике, дополнении и умножении чисел с плавающей запятой не ассоциативно, поскольку округление ошибок введено, когда ценности несходного размера объединены.

Чтобы иллюстрировать это, рассмотрите представление с плавающей запятой с 4-битной мантиссой:

(1.000×2 +

1.000×2) +

1.000×2 =

1.000×2 +

1.000×2 =

1.00×2

1.000×2 +

(1.000×2 +

1.000×2) =

1.000×2 +

1.00×2 =

1.00×2

Даже при том, что большинство компьютеров вычисляет с 24 или 53 битами мантиссы, это — важный источник округления ошибки, и подходы, такие как Алгоритм Суммирования Kahan являются способами минимизировать ошибки. Это может быть особенно проблематично в параллельном вычислении.

Примечание для неассоциативных операций

В целом круглые скобки должны использоваться, чтобы указать на заказ оценки, если неассоциативная операция появляется несколько раз в выражении. Однако математики договариваются об особом заказе оценки для нескольких общих неассоциативных операций. Это — просто письменное соглашение избежать круглых скобок.

Лево-ассоциативная операция — неассоциативная операция, которая традиционно оценена слева направо, т.е.,

\left.

\begin {матричный }\

x*y*z = (x*y) *z\qquad\qquad\quad \,

\\

w*x*y*z = (w*x) *y) *z\quad

\\

\mbox {и т.д. }\\qquad\qquad\qquad\qquad\qquad\qquad\\\,

\end {матричный }\

\right\}\

\mbox {для всех} w, x, y, z\in S

в то время как правильно-ассоциативная операция традиционно оценена справа налево:

\left.

\begin {матричный }\

x*y*z=x* (y*z) \qquad\qquad\quad \,

\\

w*x*y*z=w* (x* (y*z)) \quad

\\

\mbox {и т.д. }\\qquad\qquad\qquad\qquad\qquad\qquad\\\,

\end {матричный }\

\right\}\

\mbox {для всех} w, x, y, z\in S

Происходят и лево-ассоциативные и правильно-ассоциативные операции. Лево-ассоциативные операции включают следующее:

Вычитание и подразделение действительных чисел:

::

::

Применение функции:

::

Примечание:This может быть мотивировано приправляющим карри изоморфизмом.

Правильно-ассоциативные операции включают следующее:

Возведение в степень действительных чисел:

::

Причина:The возведение в степень правильно-ассоциативно, состоит в том, что повторная лево-ассоциативная операция по возведению в степень была бы менее полезной. Многократные появления могли (и быть) быть переписанными с умножением:

::

::

::

:Using правильно-ассоциативное примечание для этих операций может быть мотивирован корреспонденцией Карри-Howard и приправляющим карри изоморфизмом.

Неассоциативные операции, для которых не определен никакой обычный заказ оценки, включают следующий.

Взятие Взаимного продукта трех векторов:

::

Взятие попарного среднего числа действительных чисел:

::

Взятие относительного дополнения наборов не является тем же самым как. (Сравните материальное незначение в логике.)

Примеры

Некоторые примеры ассоциативных операций включают следующий.

• Связь трех последовательностей, может быть вычислена, связав первые две последовательности (дающие) и прилагающие третью последовательность , или присоединившись к второй и третьей последовательности (предоставление) и связывание первой последовательности с результатом. Эти два метода приводят к тому же самому результату; связь последовательности ассоциативная (но не коммутативная).
• В арифметике дополнение и умножение действительных чисел ассоциативны; т.е.,

::

\left.

\begin {матричный }\

(x+y) +z=x + (y+z) =x+y+z\quad

\\

(x \, y) z=x (y \, z) =x \, y \, z\qquad\qquad\qquad\quad\\\,

\end {матричный }\

\right\}\

\mbox {для всех} x, y, z\in\mathbb {R}.

:Because ассоциативности, группирующиеся круглые скобки могут быть опущены без двусмысленности.

• Дополнение и умножение комплексных чисел и кватернионов ассоциативны. Добавление octonions также ассоциативно, но умножение octonions неассоциативно.
• Самый большой общий делитель и наименьшее количество функций общего множителя действуют ассоциативно.

::

\left.

\begin {матричный }\

\operatorname {GCD} (\operatorname {GCD} (x, y), z) =

\operatorname {GCD} (x, \operatorname {GCD} (y, z)) =

\operatorname {GCD} (x, y, z) \\quad

\\

\operatorname {LCM} (\operatorname {LCM} (x, y), z) =

\operatorname {LCM} (x, \operatorname {LCM} (y, z)) =

\operatorname {LCM} (x, y, z) \quad

\end {матричный }\

\right\}\\mbox {для всех} x, y, z\in\mathbb {Z}.

Взятие пересечения или союза наборов:

::

\left.

\begin {матричный }\

(A\cap B) \cap C=A\cap (B\cap C) =A\cap B\cap C\quad

\\

(A\cup B) \cup C=A\cup (B\cup C) =A\cup B\cup C\quad

\end {матричный }\

\right\}\\mbox {для всех наборов} A, B, C.

Если M — некоторый набор, и S обозначает набор всех функций от M до M, то операция функционального состава на S ассоциативна:

::

Немного более широко, учитывая четыре набора M, N, P и Q, с h: M к N, g: N к P и f: P к Q, тогда

::

: как прежде. Короче говоря, состав карт всегда ассоциативен.

Рассмотрите набор с тремя элементами, A, B, и C. Следующая операция:

Ассоциативный:is. Таким образом, например, (до н.э) = (AB) C = A. Это отображение не коммутативное.

Поскольку матрицы представляют линейные функции преобразования с матричным умножением, представляющим функциональный состав, можно немедленно прийти к заключению, что матричное умножение ассоциативно.

Порядок выполнения арифметических действий в выражениях со скобками

Выражения часто содержат . В этом случае правило, задающее порядок выполнения действий в выражениях со скобками, формулируется так: сначала выполняются действия в скобках, при этом также по порядку слева направо выполняется умножение и деление, затем – сложение и вычитание.

Итак, выражения в скобках рассматриваются как составные части исходного выражения, и в них сохраняется уже известный нам порядок выполнения действий. Рассмотрим решения примеров для большей ясности.

Пример.

Выполните указанные действия 5+(7−2·3)·(6−4):2.

Решение.

Выражение содержит скобки, поэтому сначала выполним действия в выражениях, заключенных в эти скобки. Начнем с выражения 7−2·3. В нем нужно сначала выполнить умножение, и только потом вычитание, имеем 7−2·3=7−6=1. Переходим ко второму выражению в скобках 6−4. Здесь лишь одно действие – вычитание, выполняем его 6−4=2.

Подставляем полученные значения в исходное выражение: 5+(7−2·3)·(6−4):2=5+1·2:2. В полученном выражении сначала выполняем слева направо умножение и деление, затем – вычитание, получаем 5+1·2:2=5+2:2=5+1=6. На этом все действия выполнены, мы придерживались такого порядка их выполнения: 5+(7−2·3)·(6−4):2.

Запишем краткое решение: 5+(7−2·3)·(6−4):2=5+1·2:2=5+1=6.

Ответ:

5+(7−2·3)·(6−4):2=6.

Бывает, что выражение содержит скобки в скобках. Этого бояться не стоит, нужно лишь последовательно применять озвученное правило выполнения действий в выражениях со скобками. Покажем решение примера.

Пример.

Выполните действия в выражении 4+(3+1+4·(2+3)).

Решение.

Это выражение со скобками, это означает, что выполнение действий нужно начинать с выражения в скобках, то есть, с 3+1+4·(2+3). Это выражение также содержит скобки, поэтому нужно сначала выполнить действия в них. Сделаем это: 2+3=5. Подставив найденное значение, получаем 3+1+4·5. В этом выражении сначала выполняем умножение, затем – сложение, имеем 3+1+4·5=3+1+20=24. Исходное значение, после подстановки этого значения, принимает вид 4+24, и остается лишь закончить выполнение действий: 4+24=28.

Ответ:

4+(3+1+4·(2+3))=28.

Вообще, когда в выражении присутствуют скобки в скобках, то часто бывает удобно выполнение действий начинать с внутренних скобок и продвигаться к внешним.

Например, пусть нам нужно выполнить действия в выражении (4+(4+(4−6:2))−1)−1. Сначала выполняем действия во внутренних скобках, так как 4−6:2=4−3=1, то после этого исходное выражение примет вид (4+(4+1)−1)−1. Опять выполняем действие во внутренних скобках, так как 4+1=5, то приходим к следующему выражению (4+5−1)−1. Опять выполняем действия в скобках: 4+5−1=8, при этом приходим к разности 8−1, которая равна 7.

Источники:

• В. В. Воеводин «Линейная алгебра» Издание 2, 1980 года, стр. 9-13
• А. И. Кострыкин «Введение в алгебру. Основы алгебры», 1994 года, стр. 155-160
• А. Г. Курош «Курс высшей алгебры» издание 9, 1968 года, стр. 147-161
• Белозеров Г.С. Конспект лекций

Лимит времени:

из 5 заданий окончено

Вопросы:

1. 1
2. 2
3. 3
4. 4
5. 5

Информация

Основные свойства бинарных алгебраических операций.

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Результаты

Правильных ответов: из 5

Ваше время:

Время вышло

Вы набрали из баллов ()

Средний результат
Ваш результат

максимум из 30 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Ваш результат был записан в таблицу лидеров

Капча:

1. 1
2. 2
3. 3
4. 4
5. 5

1. С ответом

2. С отметкой о просмотре

1. Задание 1 из 5

   1.

   Количество баллов: 10

   Как ещё называют коммутативный, ассоциативный и дистрибутивный законы? Разместите ответы в соответствующем порядке, не подходящий ни к чему разместите в конце.

   • Переместительный

   • Сочетательный

   • Распределительный

   • Исключительный

2. Задание 2 из 5

   Количество баллов: 5

   Какой закон устанавливает связь сразу между двумя операциями?

   • Дистрибутивность

   • Коммутативность

   • Ассоциативность

3. Задание 3 из 5

   Количество баллов: 5

   Ассоциативно ли умножение матриц над полем вещественных чисел?

   • Да

   • Нет

4. Задание 4 из 5

   Количество баллов: 5

   Дистрибутивно ли умножение относительно сложения матриц над полем комплексных чисел?

   • Да

   • Нет, ведь умножение матриц над полем вещественных чисел даже не коммутативно.

5. Задание 5 из 5

   5.

   Количество баллов: 5

   Как ещё называется теорема, приведённая в примере 2?

   • Общий коммутативный закон

   • Общий ассоциативный закон

   • Общий дистрибутивный закон

максимум из 30 баллов

Место	Имя	Записано	Баллы	Результат
Таблица загружается
Нет данных

Обобщенный ассоциативный закон

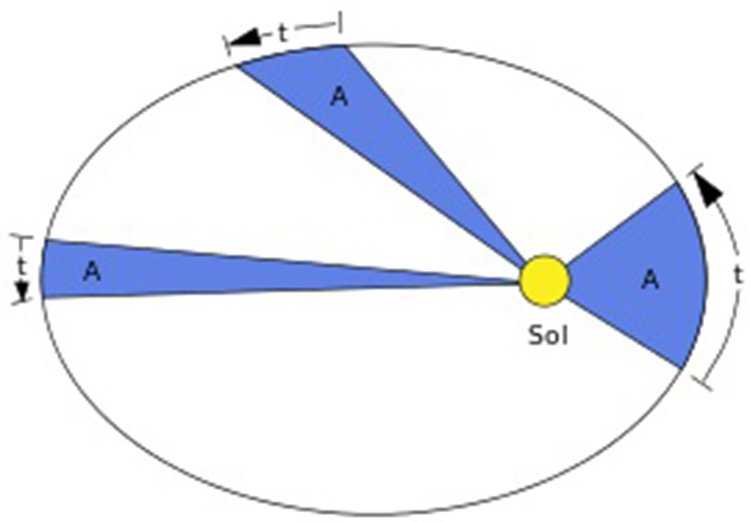
Если операция над двоичными числами — ассоциативное, повторное применение операции, приводит к тому же самому результату независимо, как действительные пары круглой скобки введены в выражение. Это называют обобщенным ассоциативным законом. Например, продукт четырех элементов может быть написан пятью возможными способами:

1. ((ab) c) d
2. (ab) (CD)
3. ((до н.э)) d
4. ((до н.э) d)
5. (b (CD))

Если операция по продукту ассоциативна, в обобщенном ассоциативном законе говорится, что все эти формулы приведут к тому же самому результату, делая круглую скобку ненужной. Таким образом продукт может быть написан однозначно как

:abcd.

Когда ряд элементов увеличивается, число возможных способов вставить круглые скобки растет быстро, но они остаются ненужными для разрешения неоднозначности.

Логическая логика

Правило замены

В стандартной функциональной правдой логической логике ассоциация или ассоциативность является двумя действительными правилами замены. Правила позволяют перемещать круглые скобки в логические выражения в логических доказательствах. Правила:

и

, где «» металогическое представление символа, «может быть заменено в доказательстве с».

Правда функциональные соединительные слова

Ассоциативность — собственность некоторых логических соединительных слов функциональной правдой логической логики. Следующие логические эквивалентности демонстрируют, что ассоциативность — собственность особых соединительных слов. Следующее — функциональные правдой тавтологии.

Ассоциативность дизъюнкции:

Ассоциативность соединения:

Ассоциативность эквивалентности:

Распределительный закон умножения

Распределительный закон умножения позволяет умножить сумму на число или число на сумму.

Рассмотрим следующее выражение:

(3 + 5) × 2

Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:

(3 + 5) = 8

В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:

8 × 2 = 16

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:

Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:

(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16

Или ещё короче:

(3 + 5) × 2 = 6 + 10 = 16

Теперь запишем распределительный закон умножения с помощью переменных:

(a + b) × c = a × c + b × c

Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.

Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×

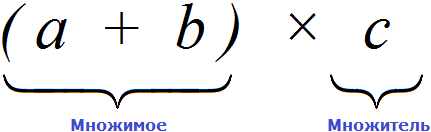
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:

c × (a + b) = c × a + c × b

Пример 2. Найти значение выражения 5 × (3 + 2)

Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:

5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25

Пример 3. Найти значение выражения 6 × (5 + 2)

Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:

6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42

Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.

Пример 4. Найти значение выражения 5 × (6 − 2)

Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20

Пример 5. Найти значение выражения 7 × (3 − 2)

Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:

7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7

Основными свойствами бинарных алгебраических операций являются:

Коммутативность (переместительность)

Свойство бинарной алгебраической операции $ \circ ,$ при котором выполняется условие: $ \forall \ x,y \in \mathbb{P}: $ $ (x\circ y)=(y\circ x) ,$ где $ \mathbb{P} $ — некоторое рассматриваемое множество.

Ассоциативность (сочетательность)

Свойство бинарной алгебраической операции $ \circ ,$ при котором выполняется условие: $ \forall \ x,y,z \in \mathbb{P}: $ $ (x\circ y)\circ z=y\circ (x\circ z) ,$ где $ \mathbb{P} $ — некоторое рассматриваемое множество.

Дистрибутивность (распределительный закон)

Свойство согласованности некоторых двух рассматриваемых алгебраических операций $ \oplus $ и $ \otimes $ на одном и том же некотором рассматриваемом множестве $ \mathbb{P} ,$ при котором выполняется условие левой: $ \forall \ x,y,z \in \mathbb{P}: $ $ x\otimes (y\oplus z) $ $ =(x\otimes y)\oplus(x\otimes z) $; и/или правой: $ (y\oplus z) \otimes x $ $ =(y\otimes x)\oplus(z\otimes x) $ дистрибутивности.

Сложение многочленов

Определение. Пусть даны многочлены $$u\left(x\right)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots+a_{2}x^{2}+a_{1}x+a_{0},$$ $$v\left(x\right)=b_{m}x^{m}+b_{m-1}x^{m-1}+\ldots+b_{2}x^{2}+b_{1}x+b_{0}.$$ Будем считать, что $n\geqslant m.$ Тогда их суммой является многочлен $$s\left(x\right)=u\left(x\right)+v\left(x\right)=c_{n}x^{n}+c_{n-1}x^{n-1}+\ldots+c_{2}x^{2}+c_{1}x+c_{0},$$ каждый коэффициент $c_{i}$ которого получается сложением соответствующих коэффициентов $a_{i}$ и $b_{i},$ $\left(i = 0, 1, \ldots, n-1, n\right).$ Причём, если $n\geqslant i>m,$ то считаем, что $b_{i}=0.$

Замечание. Можно определить и вычитание многочленов, как сложение с противоположным. будет выступать нулевой многочлен $\left(0\right),$ а противоположный данному многочлен получается заменой всех коэффициентов на противоположные: $$u\left(x\right)=a_{n}x^{n}+a_{n-1}x^{n-1}+\ldots+a_{2}x^{2}+a_{1}x+a_{0},$$ $$-u\left(x\right)=-a_{n}x^{n}-a_{n-1}x^{n-1}-\ldots-a_{2}x^{2}-a_{1}x-a_{0}.$$

Основные свойства сложения

1. Степень суммы. Степень двух многочленов меньше либо равна наибольшей из степеней слагаемых.

2. Коммутативность: $u\left(x\right)+v\left(x\right)=v\left(x\right)+u\left(x\right).$

Пусть $$u\left(x\right)+v\left(x\right)=s_{1}\left(x\right),\; v\left(x\right)+u\left(x\right)=s_{2}\left(x\right).$$ Рассмотрим коэффициенты $s_{1}\left(x\right)$ и $s_{2}\left(x\right).$ Они равны в силу коммутативности сложения чисел $\left(a_{i}+b_{i}=b_{i}+a_{i}\right),$ а значит, $s_{1}\left(x\right)=s_{2}\left(x\right),$ что доказывает коммутативность сложения многочленов.

3. Ассоциативность: $\left(u\left(x\right)+v\left(x\right)\right)+w\left(x\right)=u\left(x\right)+\left(v\left(x\right)+w\left(x\right)\right).$

Пусть коэффициенты $u\left(x\right),$ $v\left(x\right)$ и $w\left(x\right)$ равны $a_{i},$ $b_{i},$ и $c_{i}$ соответственно. Зададим их суммы: $$\left(u\left(x\right)+v\left(x\right)\right)+w\left(x\right)=f\left(x\right),$$ $$u\left(x\right)+\left(v\left(x\right)+w\left(x\right)\right)=g\left(x\right).$$ Для доказательства ассоциативности, докажем равенство $f\left(x\right)$ и $g\left(x\right).$ Рассмотрим общие формулы их коэффициентов: $$f_{i}=\left(a_{i}+b_{i}\right)+c_{i},$$ $$g_{i}=a_{i}+\left(b_{i}+c_{i}\right).$$ Аналогично , равенство этих двух многочленов следует из ассоциативности операции сложения для чисел, из чего и следует ассоциативность многочленов.