Калькулятор онлайн

Вес и объём в гранёном стакане

Стоит понимать, что объём разных жидкостей может значительно отличаться. Так же, как и сам объём посуды. Очень важную роль играет плотность вещества и его состав. Отличается и сама посудина. Чтобы проще ориентироваться, за основу будет взят стандартный гранёный стакан объёмом в 240 мл.

Сухие продукты

Часто измеряются стаканами различные крупы или другие сыпучие продукты. Вот ориентировочная таблица часто встречающихся сухих и сыпучих продуктов:

• мука – 140 г;
• сахар – 200 г;
• пудра сахарная – 120 г;
• овсянка – 100 г;
• рис длинный – 200 г;
• рис круглый – 210 г;
• какао-порошок – 100 г;
• крахмал – 200 г;
• пшено 220 г;
• соль 300 г.

Зная эти показатели, легко будет определить, какой вес подразумевается, когда речь идёт о трети кухонной утвари.

Вода

В обычном стакане воды 250 г. Но это если он налит полностью. При условиях, что он наполнен «под поясок», его объём достигает 230 грамм.

Сколько весит пустой стакан

Определить вес обычной посудины просто: её нужно просто установить на весы. Но если вдруг такой возможности нет или просто очень хочется владеть информацией, то вот:

• гранёный весит 220-230 грамм;
• другие в зависимости от толщины стекла могут быть от 170 до 230 грамм.

Если необходимо измерить на весах в ёмкости продукты, то можно отнять от показателя вес тары. Но значительно эффективнее затарить, чтобы обнулить показания на весах. Для этого нужно просто нажать «Т» на весах.

Таблица измерений стакана.

Как умножить тысячи на многозначное число

Здесь поможет система Якова Трахтенберга. Во время заключения нацистами математик нашёл способ счёта особо крупных чисел в уме.

Предупреждаю, что способ подойдёт только тем, кто наработал краткосрочную память на большой массив чисел. Поскольку вам придётся долго держать остаток в уме и параллельно делать десяток сложений.

Запомните метод как Принцип снежинки.

В качестве примера решим 5362∙2934. Алгоритм такой:

Представьте числа привычным столбиком.

1. Перемножьте конечные (2∙4) цифры сверху и снизу.

Предпоследнюю цифру при наличии держим в уме (0), последнюю отправляем в результат (8): ** *** **8.

2. Перемножьте предпоследнюю цифру верхнего числа на последнюю нижнего (6∙4) и наоборот (3∙2).

Сложите результаты с тем, что храните в уме (24+6+0=30).

Держим остаток (3), а последнее число ставим в итог слева от предыдущего (0): ** *** *08.

3. Умножьте вторую цифру верхнего числа на последнюю нижнего (3∙4) и наоборот (9∙2).

Сложите результаты (12+18=30), а к ним добавьте умноженные друг на друга третьи цифры (6∙3) и остаток в уме (30+18+3=51).

Получили десяток в уме (5) и третью с конца цифру (1): ** *** 108.

4. Умножьте первую цифру сверху на последнюю снизу (5∙4) и наоборот (2∙2).

Умножьте вторую цифру сверху на третью снизу (3∙3) и наоборот (9∙6).

Сложите четыре числа и пятое из ума (20+4+9+54+5=92).

Получили десяток в уме (9) и четвёртую с конца цифру (2): ** **2 108.

5. Умножьте первую цифру верхнего числа на третью нижнего (5∙3) и наоборот (2∙6).

Сложите результаты, а к ним добавьте умноженные друг на друга вторые числа (3∙9) и остаток в уме (15+12+27+9=63).

Получили десяток в уме (6) и пятую с конца цифру (3): ** *32 108.

6. Умножьте первую цифру верхнего числа на вторую нижнего (5∙9) и наоборот (2∙3).

Сложите результаты с остатком в уме (45+6+6=57).

Получили десяток в уме (5) и пятую с конца цифру (7): ** 732 108.

7. Умножьте первую цифру верхнего числа на первую нижнего (5∙2).

Сложите результат с остатком в уме (10+5=15).

Запишите всё число перед итоговым: 15 732 108.

Вы получили ответ.

Если ваш множитель двух- или трёхзначный, то вместо недостающих цифр нижнего ряда подставляйте нули. В таком случае последним этапом будет тот, где вы умножаете максимальное количество пар.

Принцип снежинки намного проще, чем умножать столбиком. Вам не нужно держать в уме много крупных чисел сразу.

Важна только структура: запомните нарастающий порядок умноженных пар и что с чем нужно складывать.

Единственной сложностью останется запомнить результат, который вы постепенно выстраиваете.

Чаще тренируйте память вариантами проще, например, умножением двух- и трёхзначными числами в приложении Устный счёт.

И тогда сможете считать миллионы, не коснувшись бумаги.

iPhones.ru

Превращаем мозг в суперкомпьютер.

Павел Телешевский

У меня 4 новых года: обычный, свой, WWDC и сентябрьская презентация Apple. Последний — самый ожидаемый, и ни капли за это не стыдно.
Instagram/Telegram: @tinelray

Умножение двух многозначных чисел

Если оба множителя — многозначные натуральные числа, нужно действовать следующим образом.

Рассмотрим пример 207 * 8063:

1. Сначала запишем наибольшее 8063, затем наименьшее 207. Нужно разместить цифры друг под другом справа налево:

1. Последовательно перемножаем значения разрядов. Результатом является неполное произведение.

1. Далее перемножаем десятки. Первый множитель умножим на значение разряда десятков второго и т.д. Результат запишем под чертой.

1. По аналогии действуем с сотыми. Ноль пропускаем в соответствии с правилом. Так получилось второе неполное произведение:

1. Далее складываем два произведения в столбик. 

1. Получившееся семизначное число — результат умножения исходных натуральных чисел.

Ответ: 8 063 * 207 = 1669041. 

Танк Тип 99 — видео

https://youtube.com/watch?v=zNttksoU_9o

Один из первых вариантов этого танка был продемонстрирован в 2000 году под обозначением Type 98G. В том же году была изготовлена первая партия из 40 танков. В дальнейшем выпуск танков осуществляется очень медленными темпами, в основном из-за их сложности и высокой стоимости. К настоящему времени изготовлено не более 100 единиц.

ОБТ Туре 99 представляет собой танк Туре 98 с улучшенными характеристиками: повышенной подвижностью за счет установки более мощного 1500-сильного дизельного двигателя турбонаддувом, усовершенствованной системой управления огнём, повышенной защищённостью за счёт установки встроенной динамической защиты на лобовые проекции башни и корпуса.Бронирование лобовых проекций башни и корпуса усилено за счет установки блоков встроенной динамической защиты. На первых серийных образцах блоки ДЗ устанавливались поверх основных броневых деталей. На последующих машинах они были встроены в основное бронирование. Изменялась и конфигурация блоков — они стали более скошенными с боков. Модульная конструкция бронирования позволяет быстро заменять поврежденные блоки на новые. Танк оснащен интегрированным лазерным комплексом активного противодействия JD-3.

Усовершенствованная СУО включает в себя комбинированные прицелы наводчика и командира с независимой стабилизацией, лазерный дальномер, тепловизор. цифровой баллистический вычислитель, двухплоскостной стабилизатор вооружения, набор датчиков (атмосферных условий, износа канала ствола и др.), многофункциональную панель командира с цветным индикатором и систему автосопровождения цели. Изображение от тепловизора выводится на цветные дисплеи командира и наводчика (кратность х 11,4 и х5). Кроме того, на танке установлена система навигации с инерциальным и спутниковым (GPS) каналами, данные от которых также выводятся на дисплей командира и накладываются на цифровую карту местности. Танк оснащён современной радиостанцией и ТПУ.

Установленный на танке дизельный двигатель мощностью 1500 л.с. создан на базе германского MB871 Ka501. Танк разгоняется с места до 32 км/ч всего за 12 с. Механическая планетарная трансмиссия предусматривает 7 скоростей для движения вперёд и одну задним ходом. Подвеска торсионная с гироамортизаторами.

Серийное производство. Танки Туре 99 принимали участие в военном параде в Пекине 1 октября 2009 года в ознаменование 50-летия образования КНР. По площади Таньаньмень прошли 18 боевых машин (судя по блокам ДЗ, раннего выпуска) из состава 334-го полка 112-й танковой дивизии 38-й армейской группы НОАК.

Закономерности в таблице умножения

Если родители хотят понять, как легко и быстро выучить таблицу умножения со школьником, то должны сначала научить его следующим закономерностям:

• При умножении любого числа на единицу всегда получается то же самое число.
• Все произведения при умножении на пять оканчиваются нулем или пятеркой. Это хорошо видно в столбике и строке с умножением на данное число. Если множители – нечетные числа, то произведение оканчивается на пять. Если один множитель – четное число, то результат оканчивается на ноль.
• Также существует закономерность при умножении на 10. В этом случае независимо от первого множителя результат всегда заканчивается нулем.
• Если сравнивать результаты умножения на пять и десять, то можно заметить, что первые ровно на половину меньше. Это связано с тем, что один из множителей в 2 раза меньше другого.
• Умножение на 4 – это то же самое, что двойное удвоение числа. То есть, если нужно умножить 6 на 4, то это равно 6+6=12 и 12+12=24.
• Есть определенная закономерность при умножении на 9. Первое число произведения становится больше на единицу, а второе – уменьшается на один.

Важно регулярно и многократно повторять выученную табличку с ребенком. Сначала ее просят рассказать по порядку, а потом задают вопросы вперемешку, чтобы школьник мог вспомнить и подумать

Сначала дают больше времени на раздумья, постепенно сокращая его.

Игорь (31)

Ищет: Подругу, которой смогу бесплатно помогать в таких областях, как построение отношений, похудение, исцеление с помощью некоторых дистанционных практик в области биоэнергетики. Также возможно общение по переписке на вне-эзотерические темы (про жизнь, работу и т.д.).

Как посчитать проценты, составив пропорцию

Составлять пропорции — одно из наиболее полезных умений, которому вас научили в школе. С его помощью можно посчитать любые проценты. Выглядит пропорция так:

сумма, составляющая 100% : 100% = часть суммы : доля в процентном соотношении.

Или можно записать её так: a : b = c : d.

Обычно пропорция читается как «а относится к b так же, как с относится к d». Произведение крайних членов пропорции равно произведению её средних членов. Чтобы узнать неизвестное число из этого равенства, нужно решить простейшее уравнение.

Пример 1

Для примера вычислений используем рецепт быстрого брауни. Вы хотите его приготовить и купили подходящую плитку шоколада массой 90 г, но не удержались и откусили кусочек-другой. Теперь у вас только 70 г шоколада, и вам нужно узнать, сколько масла положить вместо 200 г.

Сначала вычисляем процентную долю оставшегося шоколада.

90 г : 100% = 70 г : Х, где Х — масса оставшегося шоколада.

Х = 70 × 100 / 90 = 77,7%.

Теперь составляем пропорцию, чтобы выяснить, сколько масла нам нужно:

200 г : 100% = Х : 77,7%, где Х — нужное количество масла.

Х = 77,7 × 200 / 100 = 155,4.

Следовательно, в тесто нужно положить примерно 155 г масла.

Пример 2

Пропорция подойдёт и для расчёта выгодности скидок. Например, вы видите блузку за 1 499 рублей со скидкой 13%.

Сначала узнайте, сколько стоит блузка в процентах. Для этого отнимите 13 от 100 и получите 87%.

Составьте пропорцию: 1 499 : 100 = Х : 87.

Х = 87 × 1 499 / 100.

Заплатите 1 304,13 рубля и носите блузку с удовольствием.

Быстрое определение необходимого минимума

Представьте, что вы проходите серию из пяти тестов, для успешной сдачи которых вам необходим минимальный балл 92. Остался последний тест, а по предыдущим результаты таковы: 81, 98, 90, 93. Как вычислить необходимый минимум, который нужно получить в последнем тесте?

Для этого считаем, сколько баллов мы недобрали/перебрали в уже пройденных тестах, обозначая недобор отрицательными числами, а результаты с запасом — положительными.

Итак, 81 − 92 = −11; 98 − 92 = 6; 90 − 92 = −2; 93 − 92 = 1.

Сложив эти числа, получаем корректировку для необходимого минимума: −11 + 6 − 2 + 1 = −6.

Получается дефицит в 6 баллов, а значит, необходимый минимум увеличивается: 92 + 6 = 98. Дела плохи. 🙁

Быстрое вычисление времени, через которое денежный вклад под определённый процент удвоится

Хотите быстро узнать время, которое потребуется, чтобы ваш денежный вклад с определённой процентной ставкой удвоился? Тут также не нужен калькулятор, достаточно знать «правило 72».

Делим число 72 на нашу процентную ставку, после чего получаем приблизительный срок, через который вклад удвоится.

Если вклад сделан под 5% годовых, то потребуется 14 с небольшим лет, чтобы он удвоился.

Почему именно 72 (иногда берут 70 или 69) ? Как это работает? На эти вопросы развёрнуто ответит «Википедия».

Общие сведения

Смешанная дробь — число, состоящее из целого значения и обыкновенного дробного выражения. Они образуются в результате операции деления. Последняя состоит из трех элементов, а именно: делимого, делителя и частного. Чтобы понять смысл смешанного числа, нужно разобрать дробные величины. К ним относятся следующие виды:

1. Обыкновенные.
2. Десятичные.

Обыкновенная дробь образуется посредством комбинации делимого и делителя, т. е. состоит всего из двух элементов. В этом случае частное имеет вид десятичного дробного тождества. Иными словами, десятичная дробь — величина, полученная при делении числителя на знаменатель.

Обыкновенные дробные выражения бывают двух видов: правильными и неправильными. У первых величина числителя меньше знаменателя, а у вторых — наоборот. Десятичные дроби делятся на 3 типа: с фиксированным количеством знаков после запятой, бесконечные периодические и непериодические.

У периодических дробных величин после запятой математические символы повторяются через определенный период, который указывается в круглых скобках. Например, число 4,(3) читается следующим образом: четыре целых и три в периоде.

Следует отметить, что бесконечные непериодические дробные выражения в их полном виде невозможно записать на листе бумаги, поскольку количество разрядов достигает бесконечности. Далее необходимо рассмотреть сокращение дробей, поскольку операция применяется для оптимизации конвертации неправильного дробного тождества в смешанное число.

Свойства дробей

Дроби, как и любые числовые выражения, обладают определенными свойствами. К ним относятся:

1. Если от числителя отнять одно значение, а затем его прибавить, дробь не изменится, т. е. (Q+T-T)/Z=Q/Z.
2. При умножении и делении на эквивалентное число величина дробного тождества не изменится, т. е. (Q*T)/(Z*Т)=Q/Z.

Первое утверждение проверить очень просто. Для этой цели нужно решить следующий пример, прибавив и отняв от числителя одно и то же значение: 7/8. Доказательство имеет такой вид:

1. Записать дробь: 7/8.
2. Взять произвольный коэффициент: 5.
3. Отнять, а затем прибавить его к числителю: (7−5+5)/8.
4. Числа «-5» и «5» являются противоположными. Их сумма равна 0, т. е. 5−5=0.
5. Если прибавить нуль к любому числу, получится искомая величина: 5+0=5.
6. Математические преобразования исходной дроби: (7−5+5)/8=/8=(7+0)/8.
7. Результат совпадает с искомым значением: 7/8=7/8.

Второе утверждение доказывается таким же простым способом на дроби ½. Для этого нужно решить пример (1*8)/(2*8) по следующему нестандартному алгоритму:

1. Записать дробное тождество: ½.
2. Коэффициент — общий множитель: 8. Последний необходимо представить в виде обыкновенной дроби: 8/8.
3. Величина «8/8» эквивалентна единице, которую можно умножить на любое число без потери значения выражения.
4. Расписать дробное значение: (½) * (8/8) = (½) * 1 = ½.
5. Сравнить результат и исходное значение: ½ = ½.
6. Утверждение доказано.

Некоторые ученики делают большую ошибку, отнимая (прибавляя) к числителю и знаменателю одну величину. Чтобы они не путали 2 утверждения сокращения, нужно привести пример и решить его:

1. Записать искомое значение: ½.
2. Коэффициент: 3.
3. Прибавить значение «3» к числителю и знаменателю: (1+3)/(2+3)=4/5.
4. Превратить искомое значение и величину в третьем пункте в десятичные дроби: 0,5 и 0,8.
5. Сравнить: 0,5 < 0,8.

Упрощение выражений

Преобразование любого арифметического выражения начинается с упрощения. Последнее применяется для уменьшения расчетов, при которых возникают ошибки. Упростить выражение — значит, сделать его более читабельным и предоставить возможность дальнейшего применения при расчетах. Иными словами, каждый результат должен «подгоняться» под мировой стандарт. Для сокращения дробей обыкновенного типа рекомендуется использовать такие правила:

1. Вынесения общего множителя за скобки и сокращение на него.
2. Формулы сокращенного умножения.
3. Приведение подобных слагаемых.

Первое правило позволяет найти единый множитель всего дробного выражения. После этого его можно будет разделить на одно и то же число. Формулы сокращенного умножения применяются также для реализации первого правила. Суть метода заключается в использовании специальных соотношений. Например, математическое выражение «1−25t 2 » выглядит таким образом: (1−5t)(1+5t).

После раскрытия скобок реализовывается третье правило — приведение подобных слагаемых. Они группируются по наличию однотипных элементов. Например, выражение 4t-4+t+t 2 −3+2t 2 имеет следующие одинаковые компоненты, которые группируются в скобках: (2t 2 +t 2 )+(4t+t)-(4+3). Если приводить подобные элементы, выражение упрощается, т. е. 3t 2 +5t-7.

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
5	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
.	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
+	знак плюс	Сложение чисел (целые, десятичные дроби)
—	знак минус	Вычитание чисел (целые, десятичные дроби)
÷	знак деления	Деление чисел (целые, десятичные дроби)
х	знак умножения	Умножение чисел (целые, десятичные дроби)
√	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
x2	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
1/x	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
%	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
(	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
)	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
±	плюс минус	Меняет знак на противоположный
=	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
←	удаление символа	Удаляет последний символ
С	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Действия с дробями

Дробь представляет собой часть целого или, в более общем смысле, любое количество равных частей. Обычная (простая) дробь состоит из числителя, отображаемого над чертой (или перед косой чертой), и ненулевого знаменателя, отображаемого ниже (или после) черты. Действия с дробями производятся так же, как и с целыми числами.

1 ÷ 2 &plus; 1 ÷ 4 =

Десятичные дроби

Десятичная дробь — это дробь, знаменатель которой не указан явно, но понимается как целое число, равное десяти в степени один (10), два (100), три (1000) и так далее.

. 2 &plus; . 3 =

Нахождение обратного числа

Обратное число к x, обозначаемое 1/x или x-1, представляет собой число, которое при умножении на x дает единицу.

2 1/x =

Умножение многозначных чисел на многозначные

Умножение многозначных чисел на многозначные происходит таким же образом, как и умножение многозначных на однозначные. Каждая цифра многозначного числа умножается на каждую цифру другого многозначного числа. Единственное отличие заключается в том, что в конце образуется своего рода лесенка ответов, которые надо сложить. Рассмотрим несколько примеров, чтобы хорошо понять это.

Пример 1. Найти значение выражения 12 × 14

Записываем данное выражение в столбик — единицы под единицами, десятки десятками:

Теперь умножаем каждую цифру числа 12 на каждую цифру числа 14. Делать это надо по-очереди, начав с четвёрки. В результате таких действий мы приходим к умножению многозначного числа на однозначное, которое проходили ранее:

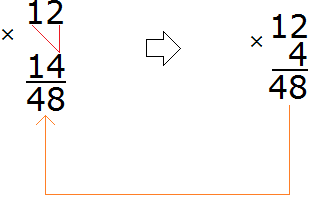
Умножив 12 на 4, мы получили число 48, которое записали таким образом, чтобы разряд единиц этого числа оказался под четверкой, на которую мы умножали число 12.

Теперь умножаем 12 на 1:

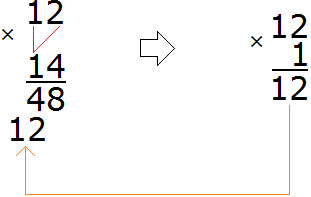
Умножив 12 на 1 мы получили число 12 и записали его таким образом, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножали число 12.

Мы получили лесенку ответов 48 и 12, которую надо сложить. Складываем и получаем ответ 168

В данном примере множитель 14 это четыре единицы и один десяток. Тогда умножение 12 на 14 можно понимать как увеличение числа 12 в четыре раза и в десять раз. Этим и объясняется появление лесенки в конце решения. Давайте посмотрим как это выглядит на каждом этапе:

Увеличим число 12 в четыре раза, получим число 48

Увеличим число 12 в десять раз, получим число 120. Записываем 120 так, чтобы можно было сложить единицы этого числа с единицами числа 48, а десятки числа 120 можно было сложить с десятками числа 48

Теперь сложим получившуюся лесенку ответов. Единицы сложим с единицами, десятки с десятками, сотни с сотнями. В результате образуется окончательный ответ:

Но чаще всего множитель не группируется с помощью разрядов, и умножение выполняют, умножая каждую цифру множимого на каждую цифру множителя.

Пример 2. Найти значение выражения 25 × 36

Записываем данное выражение в столбик

Умножаем каждую цифру числа 25 на каждую цифру числа 36.

Умножим 25 на 6:

Умножаем 25 на 3:

Теперь сложим получившуюся лесенку:

Получили ответ 900.

Рассмотрим большой и сложный пример на умножение: 12305 × 5641. Будем придерживаться ранее изученных правил.

Сначала записываем в столбик данное выражение

Теперь начинаем умножать. Число 12305 надо умножить на каждую цифру числа 5641.

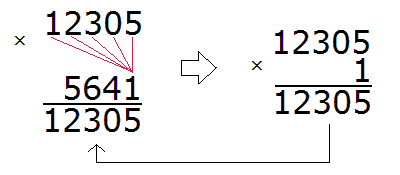
Умножив 12305 на 1, мы получили 12305 и записали это число так, чтобы разряд единиц этого числа оказался под единицей, на которую мы умножили 12305.

Теперь умножаем 12305 на следующую цифру 4:

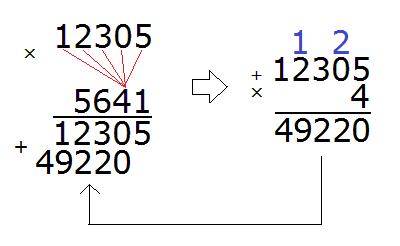Умножив 12305 на 4, мы получили 49220 и записали это число так, чтобы разряд единиц этого числа оказался под четверкой, на которую умножали 12305.

Умножаем 12305 на следующую цифру 6:

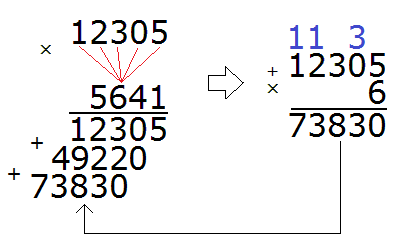
Умножив 12305 на 6, мы получили 73830 и записали это число так, чтобы разряд единиц этого числа оказался под шестёркой, на которую мы умножали 12305.

Теперь умножаем 12305 на последнюю цифру 5:

Умножив 12305 на 5, мы получили 61525 и записали это число так, чтобы разряд единиц этого числа оказался под пятёркой, на которую умножали 12305.

В результате мы получили большую лесенку, которую надо сложить. Складываем:

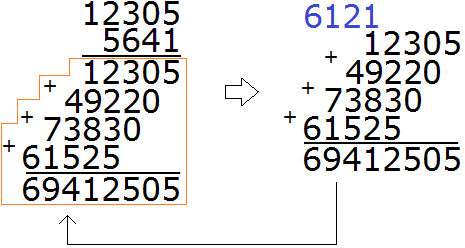
Получили окончательный ответ 69412505.

Если вы поняли этот пример, то можно сказать, что умножение больших чисел вы усвоили на отлично.

На этом урок по умножению можно завершить. Обязательно потренируйтесь, решив несколько примеров, которые даны ниже.

Важно отметить, что все эти стрелки и подробные решения, как на картинках в «боевых условиях» рисовать не принято. Нужно уметь сразу записывать ответы, выполняя в уме все вычисления

Исключением является то, если человек давно не занимался математикой или никогда ею не занимался. В таком случае можно рисовать для себя стрелки и другие вспомогательные схемы для хорошего усвоения материала.

Как посчитать проценты с помощью онлайн-сервисов

Не все проценты можно посчитать в уме и даже на калькуляторе. Если речь идёт о доходности вклада, переплатах по ипотеке или налогах, требуются сложные формулы. Они учтены в некоторых онлайн-сервисах.

Planetcalc

На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.

Ещё один сервис с калькуляторами на любой вкус.

Allcalc

Каталог онлайн-калькуляторов, 60 из которых предназначены для подсчёта финансов. Можно вычислить налоги и пени, размер субсидии на ЖКУ и многое другое.

Схема расчета

Для того, чтобы подсчитать произведение двух чисел, вам необходимо соприкоснуться двумя пальцами, числа которых соответствуют цифрам, которые вам необходимо умножить.

Например, если вы хотите высчитать, чему будет равно 7 * 6, вам необходимо коснуться безымянным пальцем левой руки (поскольку она представляет цифру слева) мизинца правой руки, поскольку он означает цифру справа. Опять же, помните, что каждый палец представляет собой число, и в этом случае ваш безымянный палец представляет семь, а ваш мизинец представляет шесть. Поэтому вам нужно соединить их чтобы решить эту математическую проблему.

Возможно, вам придется странным образом сгибать свое запястье, чтобы подсчитать произведение двух чисел! А кто говорил, что будет легко?

Для того чтобы убедиться, что вы правильно поняли технику таблицы умножения на пальцах на шесть, семь, восемь и десять, проверьте себя. Если вам необходимо вычислить, чему будет равно произведение 9 и 7, то какие пальцы вы бы соединили? Подумайте! Ответ будет в следующем предложении.

Итак, считайте, что вы выучили таблицу умножения на пальцах на шесть, семь, восемь и десять, если в качестве ответа, какие пальцы вам необходимо соединить, чтобы высчитать, чему равно произведение 9 и 7, вы выбрали указательный палец вашей левой руки и безымянный палец правой руки. Дело за малым!