Задача о восьми ферзях

История

В ранней версии шахмат, эволюционировавшей из шатранджа и в таком виде заимствованной из арабского мира в Европе, ферзь был слабейшей фигурой, перемещавшейся только на одно поле по диагонали. В Средние века, чтобы ускорить темп игры, ферзь получил дополнительную возможность: своим первым ходом ферзь мог «прыгнуть» на два поля по диагонали, горизонтали и вертикали (это правило видоизменялось в зависимости от региона). В конце XV века появилась модификация шахмат с современным ходом ферзя (тогда же был приведён к современному виду и ход слона, что радикально изменило до того медлительную игру. С новыми правилами стало возможно в несколько ходов вывести фигуры на атакующие позиции и даже проводить в начале партии матовые атаки, а возможность превращения пешки в сильнейшую фигуру вынудила пересмотреть и роль пешек. В источниках конца XV века фиксируются упоминания «шахмат ферзя» (например, исп. axedres de la dama), а в итальянском новая фигура получила имя rabiosa («бешеная»), а шахматы, соответственно, итал. scacchi alla rabiosa, то есть «бешеные шахматы».

В России была распространена практика наделять ферзя в дополнение к обычным ходам ещё и ходом коня. Об этом в конце XVIII века писал путешественник Уильям Кокс, а в 1821 году — шахматист Иван Бутримов. Согласно «Толковому словарю живого великорусского языка» В. И. Даля (статья «Ферзь»), в этом случае фигуру называли «ферзь всяческая».

Решения

Простое решение методом перебора — просто вручную удвоить и добавить каждый шаг в серии:

Т64{\ displaystyle T_ {64}} = 1 + 2 + 4 + ….. + 9,223,372,036,854,775,808 = 18,446,744,073,709,551,615

где — общее количество зерен.Т64{\ displaystyle T_ {64}}

Ряд может быть выражен с помощью показателей:

Т64знак равно2+21+22+⋯+263{\ displaystyle T_ {64} = 2 ^ {0} + 2 ^ {1} + 2 ^ {2} + \ cdots + 2 ^ {63}}

и, представленный обозначением заглавной буквы как:

∑язнак равно632я.{\ Displaystyle \ сумма _ {я = 0} ^ {63} 2 ^ {я}. \,}

Это также может быть решено намного проще, используя:

Т64знак равно264-1.{\ Displaystyle T_ {64} = 2 ^ {64} -1. \,}

Доказательством чего является:

sзнак равно2+21+22+⋯+263.{\ displaystyle s = 2 ^ {0} + 2 ^ {1} + 2 ^ {2} + \ cdots + 2 ^ {63}.}

Умножьте каждую сторону на 2:

2sзнак равно21+22+23+⋯+263+264.{\ displaystyle 2s = 2 ^ {1} + 2 ^ {2} + 2 ^ {3} + \ cdots + 2 ^ {63} + 2 ^ {64}.}

Вычтите исходную серию с каждой стороны:

2s-sзнак равно264-2{\ displaystyle 2s-s = 2 ^ {64} -2 ^ {0}}

∴sзнак равно264-1.{\ displaystyle \, следовательно, s = 2 ^ {64} -1. \,}

Вышеприведенное решение является частным случаем суммы геометрического ряда, задаваемого формулой

а+ар+ар2+ар3+⋯+арп-1знак равно∑kзнак равноп-1арkзнак равноа1-рп1-р,{\ displaystyle a + ar + ar ^ {2} + ar ^ {3} + \ cdots + ar ^ {n-1} = \ sum _ {k = 0} ^ {n-1} ar ^ {k} = а \, {\ frac {1-r ^ {n}} {1-r}},}

где — первый член ряда, — обыкновенное отношение и — количество членов.
а{\ displaystyle a}р{\ displaystyle r}п{\ displaystyle n}

В этой задаче , и .
азнак равно1{\ displaystyle a = 1}рзнак равно2{\ displaystyle r = 2}пзнак равно64{\ displaystyle n = 64}

Упражнение по работе над этой проблемой может быть использовано для объяснения и демонстрации экспонент и быстрого роста экспоненциальных и геометрических последовательностей. Его также можно использовать для иллюстрации сигма-обозначений . Выраженный в показателях, геометрический ряд выглядит следующим образом: 2  + 2 1  + 2 2
 + 2 3  + … и так далее, вплоть до 2 63 . Основание каждого возведения в степень, «2», выражает удвоение в каждом квадрате, а показатели степени представляют положение каждого квадрата (0 для первого квадрата, 1 для второго и т. Д.).

Число зерен — 64-е число Мерсенна .

Формулировка [ править | править код ]

В более «математическом» виде задача может быть сформулирована несколькими способами, например, так: «Заполнить матрицу размером 8×8 нулями и единицами таким образом, чтобы сумма всех элементов матрицы была равна 8, при этом сумма элементов ни в одном столбце, строке или диагональном ряде матрицы не превышала единицы».

Конечная цель, поставленная перед решающим задачу, может формулироваться в нескольких вариантах:

• Построить одно, любое решение задачи.
• Аналитически доказать, что решение существует.
• Определить количество решений.
• Построить все возможные решения.
• Одна из типовых задач по программированию алгоритмов перебора: создать компьютерную программу, находящую все возможные решения задачи.

Иногда постановка задачи требует нахождения способов расстановки N ферзей на доске N×N клеток (при этом при 1 Особенности решения

Общее число возможных расположений 8 ферзей на 64-клеточной доске равно 4 426 165 368 = (64!/(8!(64-8)!)). Общее число возможных расположений, удовлетворяющих условию задачи, равно 92. Интересно отметить, что эти 92 расположения разбиваются на 12 групп: 11 групп по 8 и одну из 4 расположений. Положения внутри групп получаются из одного положения путём преобразований симметрии: отражения от вертикальной и горизонтальной осей, отражения от диагоналей доски и поворотов на 90, 180 и 270 градусов. Пары расположений, симметричные относительно горизонтальной оси, имеют сумму номеров, равную 93, то есть для каждой группы эта сумма равна 93×4.

Современные компьютеры уже позволяют произвести решение задачи (нахождение любого или всех решений) путём прямого перебора всех возможных вариантов расстановки, но обычно такое решение считается некорректным, и от решающего задачу требуется найти алгоритм, который позволял бы существенно сократить объём перебора. Например, очевидно, что на одной горизонтали или вертикали доски не может находиться больше одного ферзя, поэтому алгоритм решения изначально не должен включать в перебор позиции, где два ферзя стоят на одной горизонтали или вертикали. Даже такое простое правило способно существенно уменьшить число возможных расположений: 16 777 216 (то есть 8 8 ) вместо 4 426 165 368 . Генерируя перестановки, которые являются решениями задачи о восьми ладьях и затем проверяя атаки по диагоналям, можно сократить число возможных расположений всего до 40 320 (то есть 8!). Однако, если условие нападения по диагонали учитывать при генерации позиций, скорость счёта возрастает на порядок.

Один из типовых алгоритмов решения задачи — использование поиска с возвратом: первый ферзь ставится на первую горизонталь, затем каждый следующий пытаются поставить на следующую так, чтобы его не били ранее установленные ферзи. Если на очередном этапе постановки свободных полей не оказывается, происходит возврат на шаг назад — переставляется ранее установленный ферзь.

Лучшие ответы

Алексей Мартыненко:

По-моему, к 2 начальным (чёрн. +бел. ) сколько угодно проведённых через всю доску пешек. Максимум, 18, значит…. Хотя все 16 пешек никак не перейдут. Выходит, что максимум 14. Интересный вопрос.

Vladimir Kovalkov:

скока не жалко

Неадекват:

9 но это из разряда фантастики

Alexander K.:

восемнадцать

Дмитрий Чагин:

Ты уже провёл все пешки за 8-ю линию? Зачем тебе с таким противником ещё хотя бы один ферзь?

Владислав Соколов:

С начала игры 2 (чёрный и белый) , а затем если все пешки провести в дамки, о 16! Итого 18! Но это что-то за гранью фантастики!

Фрифе:

64 ферзя, на каждую клетку.

Ефим Фёдоров:

Невозможно вычислить (стоит лишь отвлечься от «правил шахматной игры», «пропорциональности» в размерах шахматных фигур и шахматной доски, других устоявшихся в сознании стереотипов) .Согласно «правилам шахматной игры» можно ответить, напр. , на вопрос «какое максимальное количество ферзей в процессе партии может одновременно сосуществовать? «Очевидно тогда, что если игроки будут стремиться лишь максимизировать число ферзей (а, напр. не «выиграть партию»), то ферзей не может быть менее двух, ведь игроки будут стремиться сохранить уже имеющихся у них ферзей. Очевидно также, что игроки постараются сберечь все пешки, в надежде каждую из них «провести в ферзи» и увеличить тем число ферзей до максимального значения, равного восемнадцати.

Максим Сидоров:

А где их взять то больше 2-х? В комплекте всего 2 ферзя!

Ответы знатоков

Crazyuk:

Да, когда проведешь свою пешку через поле….

Gafan Radikov:

Да 1 черный 2 белый

Inkognito:

ну конечно, два и есть, один белый, другой чёрный.

Эдуард Толочьянц:

и 9 может быть. если всеми 8 пешками дойдешь до восьмой линии

sergeorul:

Конечно! Теоретически все 8 пешек могу превратиться в ферзей, что на практике ещё не случалось. Проходная пешка обычно превращается в самую сильную фигуру-ферзя, хотя может превратиться в любую из фигур: ладью, слона или коня.

Владимир Петухов:

Да, можно, кодекс шахматный не запрещает,можете заиметь хоть 9(1+8) ферзей. Запрещенопревращать белую пешку в черную фигуру инельзя превращать пешку в короля любого цвета.Ферзь конечно сильная фигура, но был интересныйслучай (играли две сильные шахматистки) , когдаодной из сторон вынуждено пришлось превращатьпешку в третьего коня (иначе была ничья) , и оказалосьчто три коня против одного, это выйгрыш.

Станислав Королёв:

Моежт быть 18 ферзей, если все пешки пройдут в ферзи

taste of Life:

смотря какой задачей заняты фигуры..) , классически для поля 8х8 их 8+1, но если условие (задача) и поле преобразованы (форма, размер), то и количество ферзей, естественно, изменится.

Госпожа СУДЬБА:

Если теоретически, то одинадцать.. . = )))

Марина:

Один

Шерлок Холмс:

Девять.

Шана:

Все пешки этого цвета + сам ферзь.

DoctoR:

Восемь пешек и один родной.

Главов:

Все пешки добежавшие до края доски.

Тимофей Щавелев:

Напрашивается такой ответ, что это девять ферзей: то есть это один ферзь от изначальной игры, и восемь пешек можно тоже превратить в ферзей! Но тут есть ещё и такой аспект: нигде в правилах не сказано, что пешка должна превращаться в фигуру своего цвета, а как говорится: «что не запрещено, то разрешено» ! Таким образом, белая пешка (если говорить чисто теоретически) , может превратиться в чёрного ферзя. И получается, что одного цвета может быть 17 ферзей, это один ферзь, данный изначально, плюс восемь, проведённых в ферзи, своих пешек, плюс восемь, проведённых пешек соперника, и превращённых в ферзи своего цвета.

Алексей Альбертович Федоров:

это вопрос не много не правильный…сколько ферзей одного цвета может быть в 1 партиинадо така иначе в шахматах если найти фигуры можно в каждую клетку поставить по ферзю то есть 64 ферзя… :]]]

Виды и названия

На шахматной доске располагаются 6 видов фигур. Это ферзь (королева), король, конь, слон (офицер), ладья (тура) и пешка. Каждому начинающему шахматисту нужно знать, как они называются.

Играть следует вдвоем, один соперник управляет черными фигурами, другой белыми. Каждый игрок имеет в своем распоряжении 16 боевых юнитов: 1 ферзь, 1 король, 2 ладьи, 2 коня, 2 офицера, 8 пешек. 

Король

На поле боя король является самой важной среди шахматных фигур, но одновременно самой слабой. Среди других юнитов, эта наиболее высокая и красивая

На вершине располагается нечто вроде короны.

Продумывая стратегию игры, важно всегда держать короля под надежной защитой, так как успешная атака в его сторону приводит к поражению и называется мат

Ферзь

Данную фигуру еще называют королевой. Она самая сильная на поле боя, сочетает в себе умения ладьи и офицера. В устаревшем арабском шатрандже королева считалась наиболее уязвимой и ходила по диагонали всего лишь на одну клетку. В европейских шахматах ферзь трансформировался в сильнейшую единицу. Внешний вид королевы аналогичен королю, но имеет более низкий рост. На вершине расположен небольшой шарик.

Ладья

Согласно правилам игры, с ладьей можно провести рокировку. Каждому игроку дается по две таких единицы, располагаются они на краях поля.

Ладья — это тяжелая фигура, внешне напоминает круглую башню. Европейское название — тура, что означает крепостная башня. В различных вариациях шахматной игры внешний вид и название ладьи сильно отличались. Например, в чатуранге ее именовали колесницей (ратх). В шатрандже ладья носила название — рух и означало птицу рух (это персонаж из фольклора арабов). На Руси данная фигура выполнялась наподобие судна (ладьи), откуда и возникло привычное нам сегодня название.

Слон

Офицер передвигается диагонально. В старых шахматах слон ходил диагонально через одну клетку и перепрыгивал через стоящие рядом юниты. Учитывая геометрию доски, он может двигаться только по клеткам одного цвета. В зависимости от того, на каком поле расставлены фигуры, они могут быть черными или белыми.

Начиная игру, шахматисты имеют в своем распоряжении по два слона, стоящих на разных по цвету клетках. Как и конь, слон считается легкой фигурой. По высоте офицер ниже ферзя, верхушка оформлена в виде капли. Такой внешний вид напоминает головной убор церковнослужителя. Европейское название слона — bishop, что переводится как епископ.

Конь

Конь — это единственный юнит, который не ходит строго по прямой или диагонали. Данная единица перемещается буквой «Г» или «L», при этом она перепрыгивает союзные или вражеские фигуры. Ход коня не изменился со времен первых шахмат. Каждый игрок начинает партию с двумя конями, размещенными между ладьей и слоном. Эту фигуру сложно перепутать с какой-либо другой, так как она имеет вид конской головы на небольшом пьедестале. Европейское название — рыцарь.

Пешка

Это единственная единица, которая по-разному ходит и атакует. Если во время партии пешка достигает последней горизонтали поля, она становится любой фигурой по усмотрению шахматиста, как правило, игроки выбирают ферзя.

Начиная партию, соперники имеют в своем распоряжении 8 пешек, они располагаются по второй горизонтали и прикрывают более ценные шахматные фигуры. Внешне пешка отличается небольшой высотой, верхушка фигуры украшена шаром.

Несмотря на то, что пешка считается одной из самых слабых фигур на доске, не стоит недооценивать ее роль. Именно эти единицы составляют основу обороны шахматиста.

Варианты шахмат

Как научиться играть в шахматы мы разобрались, теперь переходим к разным вариантам этих интеллектуальных игровых баталий.

Классика

Классическая игра имеет определенные ограничения во времени. Длительность партии составляет не менее часа. Именно столько времени выделяется игрокам на то, чтобы обдумать перемещения и выиграть противника. Чаще всего контроль выставляется на полтора часа, в течение которых игрокам нужно сделать 40 ходов. Далее возможны варианты:

• 30 минут до конца настольной битвы;
• Плюс 20 минут за каждый сделанный удачный ход и т.д.

Если мат до окончания максимального времени партии не поставлен, объявляется ничья.

Пуля

В этом варианте действуют все правила классики, но временной контроль значительно ужесточен. На обдумывание каждому игроку выделяется время от 10 до 60 секунд. За каждый выполненный ход участникам партии добавляются не минуты, а секунды.

Блиц

Блиц шахматы тоже имеют временной регламент. На обдумывание каждого хода игрокам выделяется не более 5 минут. Это самая популярная игра в шахматы на спортивных соревнованиях. Проходит она довольно быстро, требуя от игроков собранности и максимальной концентрации внимания на игровом поле.

Шахматы – 960 (Фишера)

Правила для этого варианты – стандартные. От классики они отличаются главным образом начальной позицией на крайних горизонталях. Раскладка выполняется случайным образом, выбранным из 960 возможных. Все остальные правила будут похожи на классический вариант. Это касается:

• Рокировки;
• Взятия на проходе;
• Признания ничьи;
• Шаха и мата.

Основным отличием является разнообразие вариантов начала партии. Далее партия идет по стандартным правилам с ограничением по времени.

Еще один взгляд на проблему «жизнь без последовательностей». Часть вторая (практическая) Промо

В [1 — http://infostart.ru/public/62938/] был предложен метод корректировки списаний по партиям при изменении документов задним числом. Использование данного метода позволяет контролировать остатки при неоперативном проведении и поддерживать учет по партиям всегда в актуальном состоянии, то есть обходиться без механизма последовательности документов. Собственно метод заключался в решении задачи правильного списания по партиям как задачи линейного программирования.

В доказательство работоспособности метода приводится следующая «каркасная» конфигурация «Полигон», в которой этот метод реализован.

1 стартмани

Окончание игры, шах и мат

Мы уже разобрались с тем, с чего начать, теперь пришло время узнать, как правильно закончить. Победой считается мат сопернику. Попытки загнать его в «ловушку» – в этом и состоит суть шахматной игры. Если король оказывается под ударом, ему объявляется шах, означающий, что он вправе сделать спасающий его ход или закрыться от шаха.

Мат – это капитуляция всей шахматной армии, которая не смогла защитить своего главнокомандующего, и он попал в расставленные противником сети. Чем быстрее он поставлен, тем выше считается квалификация участника. Победу в турнирах подтверждают арбитры, внимательно следящие за ходом битвы и не допускающие ни одного невозможного хода.

Расположение фигур на доске

Фигуры в шахматах, так же как и поля, имеют два основных цвета: «белый» и «черный». У каждого игрока в начале игры должны быть одинаковые наборы боевых единиц, в которые входят:

• король (царь, князь);
• ферзь (королева, министр, ученый);
• две ладьи (башни, туры);
• два коня (всадника, рыцаря);
• два слона (офицера, епископа);
• восемь пешек (пехотинцев).

В разных культурах термины могут отличаться друг от друга, общепринятые международные названия приведены здесь без скобок. Нажимайте на них, чтобы узнать то, как ходят эти фигуры.

Далее обратите внимание, как расставляются шахматные фигуры:

Доска размещается таким образом, чтобы поле a1 находилось относительно одного из игроков в левом нижнем углу. Фигурами заполняются крайние горизонтальные ряды:

• белые расставляют на 1 и 2 рядах;
• черные на 7 и 8 рядах.

В «защищенном» центре белых размещают короля (e1) и ферзя (d1), рядом с ними слонов, за ними коней, по краям (a1,р1) ладьи, второй ряд состоит из пешек. Фигуры черных должны быть расположены симметрично в рядах 7 и 8.

Никогда нельзя путать расположение горизонтальных рядов и вертикальных, проверять это легче всего по полю a1. Так же как и клетки, фигуры должны быть на своих позициях: ферзь всегда находится на поле своего цвета (белый на белом поле (d1), черный на черном (d8)), а король справа от него.

Удобнее начинать расстановку с центральных полей и главных фигур: короля и ферзя. Ценные участники битвы заслуживают большего внимания, не правда ли? Можно включать дополнительные инструменты восприятия, голосом проговаривая позиции, на которые вы расставляете фигуры.

Запоминание ценности короля, ферзя и других фигур поможет с большим пониманием отрабатывать специальные упражнения, в которых потребуется расстановка на определенные (не стартовые) позиции.

Ферзь в шахматной партии

Ферзь из Кот-д’Ивуара, 12-й век

Шахматная фигура королевы из слоновой кости, относящейся к 11 веку.

Король или ферзь из Кот-д’Ивуара, 9-й век

Шахматная королева 11 века (фото 1905)

Каждый игрок начинает партию с одним ферзём. В начале партии ферзи занимают поля d1 (у белых) и d8 (у чёрных). Поля, которые занимают ферзи в начальной расстановке фигур, того же цвета, что и сами фигуры. В связи с этим популярно выражение «ферзь любит свой цвет», используемое при обучении начинающих игроков в шахматы.

Относительно материальной ценности ферзя и сопоставления его игровой силы с другими фигурами существуют различные оценки. В большинстве случаев считается, что материальная ценность ферзя равна примерно девяти или десяти пешкам. Таким образом, ферзь по силе превосходит ладью и лёгкую фигуру, уступает двум ладьям и примерно равен трём лёгким фигурам.

Считается, что в дебюте надо проявлять осторожность с развёртыванием ферзя, поскольку он, находясь в лагере противника, становится крайне уязвим для его фигур. Гораздо лучше ферзь проявляет свои возможности в миттельшпиле и эндшпиле

Так, считается, что в эндшпиле король с ферзём при правильной игре всегда выигрывают у короля и лёгкой фигуры, почти всегда ― у короля и ладьи, в большинстве случаев — у короля и двух лёгких фигур, а также у короля, ладьи и пешки.

Кроме того, важнейшей задачей большинства эндшпилей является продвижение пешки в ферзи: удачное выполнение этой задачи, как правило, означает выигрыш партии. В правилах игры отсутствуют ограничения на количество одновременно находящихся на доске ферзей, так что дополнительно к начальному ферзю игрок теоретически может получить ещё 8 ферзей путём превращения в них пешек. В практических партиях в большинстве случаев на доске возникает только второй ферзь у одной из сторон. Хотя известны случаи даже из партий сильных игроков, когда на доске возникали одновременно 5 или даже 6 ферзей.

При атаке на ферзя часто используется термин «гарде», однако объявление не обязательно и в официальных правилах игры отсутствует.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Как ходят

После того как изучены названия и особенности расстановки юнитов на поле, необходимо рассмотреть, как фигуры ходят в шахматах:

1. Пешка — важная особенность шахматной пехоты в том, что пешки не могут ходить назад. Данная фигура идет по прямой на одно поле вперед. Первый ход является исключением, шахматист может выставить пешку сразу на два поля. Бьет данная фигура на одно поле диагонально в любую из сторон. И хоть пешка считается самой слабой на поле, она часто решает исход боя. Когда эта единица доходит до крайней линии доски, она может стать любой фигурой, за исключением короля. При этом замена статуса пешки считается ходом.
2. Конь — это единственный юнит, который не ходит ровно по прямой или диагонали. Передвижение похоже на букву «Г» или латинскую «L». Перемещаться так конь может в любую сторону, а значит игроку доступно 8 вариантов ходов. Даже закрытым другими фигурами конь несет опасность для противника, так как может перепрыгивать другие юниты. При атаке он занимает место битой фигуры.
3. Слон — перемещается только по диагонали на любое количество полей. Атакует аналогичным образом. Слон может ходить только по тому цвету клеток, на котором он был размещен перед началом игры.
4. Ладья — ходит строго по вертикали или горизонтали на сколько угодно клеток, атакует тоже по прямой. Может участвовать в рокировке, этот прием выполняется с целью переместить короля в более защищенное место. Для этого его перемещают на два поля в сторону ладьи, а она занимает место короля. Рокировка доступна только в том случае, если перечисленные фигуры еще не ходили, а на линии нет препятствий в виде других фигур. Проводить рокировку можно в любую сторону.
5. Ферзь — может ходить по горизонтали, вертикали и диагонали, количество клеток для передвижения не ограничено. Ферзь максимально важен, поэтому данный юнит нужно беречь. Разменивать его на более слабые фигуры категорически не рекомендуется.
6. Король — самая слабая фигура в шахматах, одновременное — самая важная. Может ходить в любую сторону, но всего лишь на одну клетку. Есть два вида атаки короля. Когда данная фигура находится под ударом, но игрок может организовать ее защиту — это шах. Если же король атакован и уйти уже нет возможности, игроку объявляют мат, партия считается завершенной.

Шахматы — одна из старейших игр, которая до сих пор пользуется большой популярностью. Научиться играть несложно, для этого нужно всего лишь выучить название фигур, их сильные и слабые стороны, способы атаки и передвижения по доске.

Решение классической задачи программирования на C++. Восемь ферзей.

Эта задача — одна из очень интересных шахматных головоломок.
Условие такое: можно ли поставить восемь ферзей на пустой доске таким образом, чтобы ни один из них не «атаковал» другого, т.е. так, чтобы ни какие два ферзя не стояли на одном и том же столбце, или на одной и той же строке, или на одной и той же диагонали шахматной доски.
Решение этой задачи, как вы понимаете, существует, причём не одно. На рис.1 я показал один из возможных вариантов расстановки ферзей.
Рис.1
Решение этой задачи на компьютере не представляет большой сложности. В принципе, можно тупо перебрать все возможные варианты расстановки ферзей на доске, а затем определить подходящие. Написать такую программу не сложно, но возникает вопрос: «Сколько существует вариантов и сколько времени нужно для их перебора?» Честно говоря, считать точное количество вариантов мне было лень, но, судя по всему, ждать придется долго.
Поэтому, нужно каким-то образом определить на какую клетку ставить следующего ферзя. Например, ставить несколько ферзей в одну линию бессмысленно (это противоречит условию). Если попробовать решить задача вручную, то становится понятно, что расставить 6 – 7 ферзей не сложно. Но после этого свободных клеток (которые не «бьются» ни одним из ферзей) нет. Следовательно, ферзей нужно расставлять так, чтобы они били как можно меньше клеток. Очень хорошо если несколько разных ферзей «бьют» одни и те же клетки, но при этом не «бьют» друг друга.
Дальше все очень просто. Нужно перебрать по очереди все свободные клетки доски (те, которые не «атакует» ни один ферзь) и посчитать, сколько свободных клеток «будет» бить ферзь из данной.
Для решения задачи нам понадобиться массив accessibility. В нем мы будем хранить информацию о том, свободна данная клетка или нет. Таким образом, для того чтобы определить сколько клеток будет «бить» ферзь из заданной, нам нужно перемещать ферзя по всем возможным направлениям (их восемь) и считать свободные клетки. Для перемещения ферзя удобно использовать два одномерных массива, элементы которых указывают на сколько клеток нужно сместить ферзя при движении в выбранном направлении. Я определил их таким образом:
Нулевой элемент соответствует перемещения вправо. Первый – по диагонали вправо и вверх, и т.д. Для перемещения ферзя, например, на одну клетку вниз можно записать
Далее нужно выбрать клетку, которой соответствует наименьшее количество «выбитых» свободных клеток. Если таких клеток несколько, то выбираем одну из них случайным образом и ставим на неё ферзя (при этом нужно отметить в массиве accessibility, что соответствующие клетки заняты). Процесс повторяется до тех пор, пока не будут установлены все 8 ферзей.
На этом примере очень хорошо виден главный недостаток эвристического программирования – он не всегда позволяет решить задачу. Программа, работающая по данному алгоритму, находит решение примерно один раз из десяти. Этот результат, конечно, можно улучшить, если, например, выполнять анализ на несколько ходов вперёд. Но, в любом случае, такая программа не сможет гарантировать решение, мы только увеличим вероятность его нахождения.Скачать программуСкачать исходники (Для компиляции необходим Borland C++ Builder 5)

Теги: 
Решение классической задачи

Похожие новости:

• Классические задачи программирования. Путешествие коня.
• Восемь мифов про Java
• Восемь отличий профессионального web-дизайнера
• Восемь отличий профессионального web-дизайнера
• Дорабатываем CGridView под свои задачи

Как ходит и бьет пешка?

Первый ход у пешек является особенным. Обычно, именно эта фигура начинает шахматную партию. Иногда партия начинается с хода коня, но такой вариант используется редко. Изначально пешка может перемещаться прямо на одну или на две клетки вперед.

Далее на поле пешки имеют возможность ходить вперед по вертикали лишь на одну клетку.

Часто в шахматных партиях пешки упираются друг в друга и продолжать движение дальше не могут. Ввиду особенностей взятия фигуры, побить противника таким образом они не имеют возможности, поэтому будут стоять так, пока им не откроется дорога или не возникнет возможность взять другую фигуру.

Взятие фигуры пешкой происходит по диагонали на одну клетку. Побить с помощью пешки можно любую фигуру, кроме короля. Таким образом, когда пешка упирается в другую фигуру и не может пойти дальше, она может побить расположенного по диагонали противника, чтобы изменить свое местоположение и обойти препятствие.

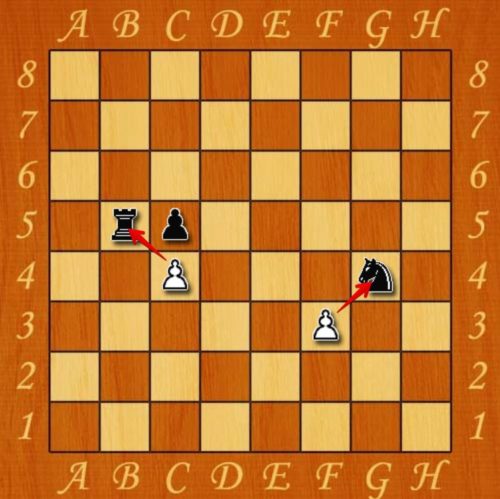
Поскольку пешка бьет по диагонали, у нее под атакой могут находиться одновременно две фигуры. Такие «вилки» существенно ослабляют противника, поскольку под ударом одновременно могут оказаться несколько значимых фигур.

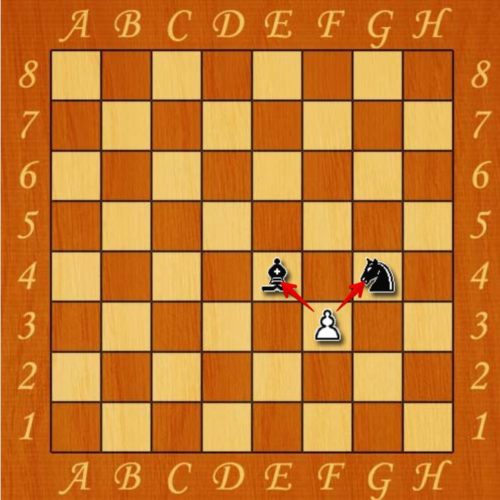
При движении пешек существует одна особенная ситуация, которая называется «взятие на проходе». При начальном положении пешки на поле, она имеет возможность делать ход сразу на два поля, проскакивая одну клетку. Если в этот момент перепрыгнутое поле находится под боем вражеской пешки, то она может побить данную фигуру.

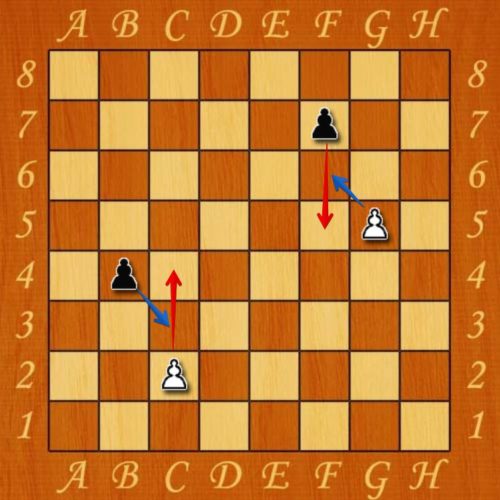
Такой прием можно применять только для взятия пешек – с остальными фигурами данное правило не работает. Также прием взятия на проходе можно применять только в ответ на движение пешки противника. Это правило известно многим, но на практике о нем часто забывают, что может привести к потере собственной фигуры.

Вот видео, где подробно рассказано, про взятие на проходе.