Искусство умножения двузначных чисел в уме

Примеры на умножение в столбик

Самостоятельное решение задачек помогает быстрее запомнить правила и натренировать скорость

Неважно, в каком классе учится ребенок — в 1, 3 или 4 — эти примеры подойдут всем

Чтобы запомнить все правила, повторите метод сложения столбиком, так как один из этапов умножения состоит из сложения промежуточных результатов. А еще лучше — приходите заниматься увлекательной математикой в детскую школу Skysmart.

Вместо скучных параграфов ученики решают интерактивные задачки и головоломки с мгновенной автоматической проверкой, а еще чертят фигуры на онлайн-доске вместе с преподавателем.

Как объяснить ребенку, что такое умножение и деление

Причина непонимания умножения и деления в большинстве случаев кроется в банальном отсутствии внимательности у школьника

В раннем возрасте деткам сложно концентрировать внимание на чем-то конкретном более 15 минут, поэтому они поддаются влиянию различных отвлекающих факторов

Обратите внимание! Ребенок может стесняться задавать учителю один и тот же вопрос несколько раз, потому что боится показаться глупым в глазах окружающих. В такой ситуации нужно провести со школьником беседу, уточнить детали, которые ему непонятны после объяснения материала, и успокоить

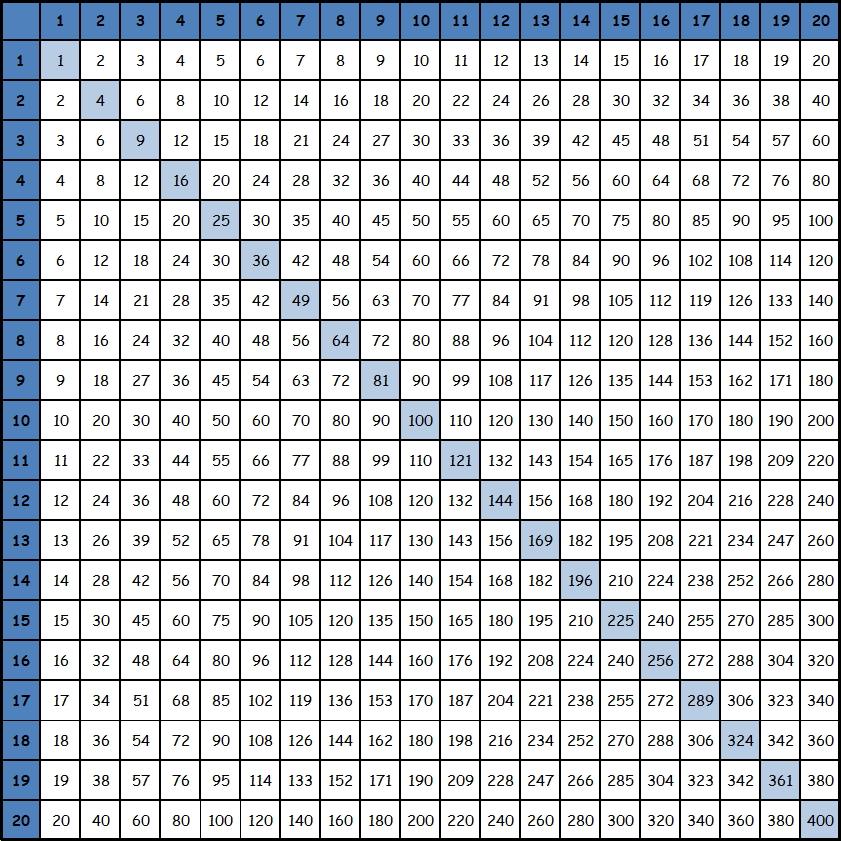
Для того чтобы объяснить ребенку понятие «умножение», для начала нужно подготовить распечатку таблицы умножения Пифагора (нарисовать ее собственноручно или распечатать на принтере). Без такой таблицы не получится разъяснить сам принцип только с помощью обычных примеров. На начальном этапе пусть ребенок сам постарается определить закономерность (желательно, чтобы это занятие стало увлекательной игрой).

Изучая данный раздел математики, детишкам должны быть известны такие простые действия, как сложение и вычитание. Разъясняя своему чаду принцип работы умножения, рекомендуется использовать самый элементарный прием. Нужно разобраться, что фраза «умножить число шесть на число два» или же «шестью два» означает то же самое, что и «шесть плюс шесть». Также следует записать пример в виде цифр для визуализации: 6*2 = 6+6.

Таблица умножения Пифагора

Объяснение принципа деления

Для того чтобы разъяснить ребенку, как нужно правильно делить, совсем необязательно использовать скучные учебники. Вместо них можно взять яблоки, конфеты и игрушки. Взрослый должен попросить карапуза разделить между тремя – четырьмя куклами пять конфеток или яблок, а далее количество фруктов следует постепенно увеличивать до 8-10.

Важно! Малыш сначала будет раскладывать предметы медленно, делая большие паузы, но кричать на него категорически запрещено, лучше запастись терпением. После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог

Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну»

После того, как сладости или фрукты были разделены между игрушками, пусть ребенок посчитает, сколько их получилось у каждой куклы и поведет итог. Если было 6 карамелек и их раздали трем куклам – каждой досталось по 2. После чего родитель должен объяснить своему ребенку, что «разделять» означает «раздать всем поровну».

Еще один игровой пример представлен делением на цифрах. Нужно сказать карапузу, что цифры – это те же фрукты или конфеты и приучать, что количество сладостей, которые следует разделить, принято называть «делимое». А люди, на которых делятся конфеты, – это «делитель».

Что еще стоит знать

Как бы стыдно мне не было, но к своим 30 годам я поняла, что очень плохо считаю в уме элементарные числа и трачу на это много времени. Этот недостаток я решила исправить и нашла на просторах интернета инструменты, которые помогли мне научиться считать в уме.

В арифметике существуют ключевые закономерности, которые необходимо довести до автоматизма.

Умножение на 9. Быстро умножить любое число на 9 можно следующим образом: сначала умножьте это число на 10 (просто добавьте 0 в конце), а затем вычтите из результата само число. Например 89*9=890-89=801. Эту операцию необходимо довести до автоматизма.

Умножение на 2

Для устного счета очень важно уметь быстро умножать любое число на 2. Для умножения на 2 не круглых чисел попробуйте округлить их до ближайших более удобных

Так 139*2 проще считать, если сначала умножить 140*2 (140*2=280). а потом вычесть 1*2=2 (именно 1 нужно прибавить к 139, чтобы получить 140) Итого: 140*2-1*2=278

Деление на 2. Для устного счета также важно уметь быстро делить любое число на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях также пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198+2) на 2 и отнять 1 (1 мы получили, разделив прибавленные 2 на 2) Итого: 198/2=200/2-2/2=100-1=99.

Деление и умножение на 4 и 8. Деление (или умножение) на 4 и 8 являются двукратным или трехкратным делением (или умножением ) на 2. Производить эти операции удобно последовательно. Например, 46*4=46*2*2=922*2=184

Умножение на 5. Умножать на 5 очень просто. Умножение на 5 и деление на 2 — это практически одно и то же. Так 88*5=440, а 88/2=44, поэтому всегда умножайте число на 5, поделив число на 2 и умножив его на 10.

Умножение на однозначные числа. Чтобы быстро считать в уме, полезно уметь умножать двузначные и трехзначные числа на однозначные. Для этого нужно умножать дву- или трехзначное чило поразрядно. Например, умножим 83*7. Для этого сначала умножим 8 на 7 (и допишем 0, так как 8 — разряд десятков) и прибавим к этому числу произведение 3 и 7. Таким образом, 83*7=80*7+3*7=560+21=581. Возьмем более сложный пример 236*3. Итак, умножаем сложное число на 3 поразрядно: 200*3+30*3+6*3=600+90+18=708.

Определение диапазонов. Чтобы не запутаться в алгоритмах и по ошибке выдать совсем неверный ответ, важно уметь строить примерный диапазон ответов. Так умножение однозначных чисел друг на друга, может дать результат не более 90 (9*9=81), двузначных — не более 10 000 (99*99 =9801), Трехзначных не более — 1 000 000 (999*999=998001)

Деление 1000 на 2,4,8,16. И наконец, полезно знать деление чисел, кратных 10 на числа, кратные двум:

100=2*500=4*250=8*125=16*62,5

Урок 4. Частные методики умножения двузначных чисел до 30

Преимуществом трех способов умножения двузначных для устного счета, описанных в прошлом уроке, состоит в том, что они универсальны для любых чисел и при хорошем навыке устного счета, они могут позволить вам достаточно быстро прийти к правильному ответу.

Однако, эффективность умножения некоторых двузначных чисел в уме может быть выше за счет меньшего количества действий при использовании специальных алгоритмов. В этом уроке вы узнаете, как можно быстро умножать любые числа до 30.

Здесь представлены специальные методики, в том числе и введение в использование опорного числа.

Умножение на 11

Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23*11, пишем 2 и 3, а между ними ставим сумму (2+3). Или короче, что 23*11= 2 (2+3) 3 = 253.

Если сумма чисел в центре дает результат больше 10, тогда добавляем единицу к первой цифре, а вместо второй цифры пишем сумму цифр умножаемого числа минус 10. Например: 29*11 = 2 (2+9) 9 = 2 (11) 9 = 319.

Умножать на 11 таким способом можно любые двузначные числа. Для наглядности приведены примеры:

81 * 11 = 8 (8+1) 1 = 891

68 * 11 = 6 (6+8) 8 = 748

Быстро умножать на 11 устно можно не только двузначные числа, но и любые другие числа — об этом читайте в данной статье, а также в книге «Система быстрого счета по Трахтенбергу».

Квадрат суммы, квадрат разности

Для того чтобы возвести в квадрат двузначное число, можно воспользоваться формулами квадрата суммы или квадрата разности. Например:

232= (20+3)2 = 202 + 2*3*20 + 32 = 400+120+9 = 529

692 = (70-1)2 = 702 – 70*2*1 + 12 = 4 900-140+1 = 4 761

Возведение в квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу дописываем 25.

152 = (1*(1+1)) 25 = 225

252 = (2*(2+1)) 25 = 625

852 = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

1552 = (15*(15+1)) 25 = (15*16)25 = 24 025

Умножение чисел до 20

1 шаг. Для примера возьмём два числа – 16 и 18. К одному из чисел прибавляем кол-во единиц второго – 16+8=24

2 шаг. Полученное число умножаем на 10 – 24*10=240

3 шаг. Далее к результату прибавляем произведение единиц 16 и 18 – 240+6*8=288

Методика умножения чисел до 20 очень проста:

Если записать короче, то:

16*18 = (16+8)*10+6*8 = 288

Доказать правильность этого метода просто: 16*18 = (10+6)*(10+8) = 10*10+10*6+10*8+6*8 = 10*(10+6+8) +6*8. Последнее выражение и является демонстрацией описанного выше метода.

По сути, этот метод является частным способом использования опорных чисел (о которых будет сказано в следующем уроке). В данном случае опорным числом является 10.

В последнем выражении доказательства видно, что именно на 10 мы умножаем скобку.

Но в качестве опорного числа можно использовать и любые другие числа, из которых наиболее удобными являются 20, 25, 50, 100… Подробнее о методе использования опорного числа читайте в следующем уроке.

Опорное число

Посмотрите на суть этого метода на примере умножения 15 и 18. Здесь удобно использовать опорное число 10. 15 больше десяти на 5, а 18 больше десяти на 8. Для того, чтобы узнать их произведение, нужно совершить следующие операции:

1. К любому из множителей прибавить число, на которое второй множитель больше опорного. То есть прибавить 8 к 15, или 5 к 18. В первом и втором случае получается одно и то же: 23.
2. Затем 23 умножаем на опорное число, то есть на 10. Ответ: 230
3. К 230 прибавляем произведение 5*8. Ответ: 270.

Подробнее о методике использования опорного числа для счета в уме читайте в следующем уроке.

Тренировка

Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время

Обратите внимание, что числа каждый раз разные

Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.

ÐгÑа загÑÑжаеÑÑÑ…

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Евгений Буянов← 3 Традиционное умножение5 Опорное число →

1PRO

Дальше — интереснее!

Не все мы выдающиеся математики. На кого-то эта наука наводит ужас при одном ее упоминании. Возможно, следующие советы помогут вам и вы сможете быстрее делать математические вычисления в уме.

Умножение на 11

Вы должны знать, что при умножении на 10 к числу прибавляется «ноль». Такой же способ существует и при умножении двузначного числа на 11.

Берем двузначное исходное число и мысленно представляем промежуток между двумя этими цифрами (для примера возьмем число 52):
5_2

Теперь складываем эти два числа, записав их еще и по середине:
5_(5+2)_2

Ответ: 572.

Если при сложении чисел в скобках получается двузначное число, то вторую цифру запомните, а вторую прибавьте к первому числу:
9_(9+9)_9
(9+1)_8_9
10_8_9
1089

Это правило работает всегда!

Быстрое возведение в квадрат

С помощью этого правила можно быстро возвести в квадрат двузначное число, оканчивающееся на 5. Просто умножьте первую цифру саму на (себя + 1), а в конце допишите 25.

Пример:
(2x(2+1)) * 25=252
2 x 3 = 6
625

Умножение на 5

Берем любое число, делим его на 2 (пополам). Если в итоге получилось целое число, приписываем 0 в конце

Если нет, то не обращайте внимание на запятую и в конце добавьте 5.

Пример:
2682 x 5 = (2682 / 2) * 5 и 0
2682 / 2 = 1341 (целое число, поэтому добавляем 0)
13410

Еще пример:
5887 x 5
2943,5 (дробное число (опускаем запятую, добавляем 5)
29435

Умножение на 9

Чтобы умножить любое число от 1 до 9 на 9, нужно посмотреть на руки. Загните палец, который соответствует умножаемому числу (например, 9х3 – загните третий палец), посчитайте пальцы до загнутого пальца (это 2), а затем после загнутого пальца (7). Ответ – 27.

Умножение на 4

Хитрость этого способа состоит в том, что нужно просто умножить число на 2, а потом снова на 2:
58 x 4 = (58 x 2) + (58 x 2) = (116) + (116) = 232

Как рассчитать чаевые

Если вы хотите оставить 15% чаевых, то можно с помощью простого способа вычислить нужную сумму. Сначала высчитайте 10% (для этого разделите число на 10). Затем добавьте получившееся число к его половине.

Пример:
15% от $25 = (10% от 25) + ((10% от 25) / 2)
$2.50 + $1.25 = $3.75

Сложное умножение

Если вам нужно перемножить большие числа, причем одно из них четное, вы можете просто перегруппировать их:
32 x 125 все равно, что:
16 x 250 все равно, что:
8 x 500 все равно, что:
4 x 1000 = 4,000

Деление на 5

Деление на 5 больших чисел — очень простое. Нужно всего лишь умножить на 2 и перенести запятую.

Пример:
195 / 5
195 * 2 = 390
Переносим запятую: 39,0 или просто 39.

Еще пример:
2978 / 5
2978 * 2 = 5956
595,6

Вычитание из 1000

Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10:
1000 — 648

• от 9 отнимите 6 = 3
• от 9 отнимите 4 = 5
• от 10 отнимите 8 = 2

Ответ: 352

Систематизированные правила умножения

• Умножение на 5: умножьте на 10 и разделите на 2.
• Умножение на 6: иногда легче умножить на 3, а потом на 2.
• Умножение на 9: умножьте на 10 и отнимите исходное число.
• Умножение на 12: умножьте на 10 и дважды прибавьте исходное число.
• Умножение на 13: умножьте на 3 и 10 раз прибавьте исходное число.
• Умножение на 14: умножьте на 7, а затем на 2.
• Умножение на 15: умножьте на 10 и 5 раз прибавьте исходное число.
• Умножение на 16: если хотите, 4 раза умножьте на 2. Или умножить на 8, а потом на 2.
• Умножение на 17: умножьте на 7 и 10 раз прибавьте исходное число.
• Умножение на 18: умножьте на 20 и дважды отнимите исходное число.
• Умножение на 19: умножьте на 20 и отнимите исходное число.
• Умножение на 24: умножьте на 8, а потом на 3.
• Умножение на 27: умножьте на 30 и 3 раза отнимите исходное число.
• Умножение на 45: умножьте на 50 и 5 раз отнимите исходное число.
• Умножение на 90: умножьте на 9 и припишите 0.
• Умножение на 98: умножьте на 100 и дважды отнимите исходное число.
• Умножение на 99: умножьте на 100 и отнимите исходное число.

Как высчитать проценты?

Пример:
необходимо вычислить 7% от 300.

Для начала необходимо понять значение слова «процент» (percent). Первая часть слова — про (per), это как 10. «PER» = «для каждого». Вторая часть — цент (cent), как 100. Например, СТОлетие = 100 лет. 100 ЦЕНТов в 1 долларе и так далее. Поэтому, ПРОЦЕНТ = ДЛЯ КАЖДОЙ СОТНИ.

Выходит, что 7% от 100 будет 7.
8% от 100 = 8.
35,73% от 100 = 35,73

Вернемся к нашему примеру (7% от 300).
7% от первой сотни = 7
7% от второй сотни — тоже 7
7% от третьей сотни — так же 7.
Итак, 7 + 7 + 7 = 21.

Если 8% от 100 = 8, то 8% от 50 = 4 (половина от 8).

Дробите каждое число, если нужно вычислить проценты из 100, если же число меньше 100, просто перенесите запятую влево.

Еще примеры:
8% от 200 = 8 + 8 = 16.
8% от 250 = 8 + 8 + 4 = 20
8% от 25 = 2,0 (передвигаем запятую влево)
15% от 300 = 15+15+15 =45
15% от 350 = 15+15+15+7,5 = 52,5

https://youtube.com/watch?v=SmKpzImyEvA

Татьяна Мельничук | Приёмы быстрого счёта

Милена Кандыбова проводит занятие на тему «Приёмы быстрого счёта» для обучающихся 11 класса

Трудно сказать, когда появились числа и как человек научился считать. Однако, наши далекие предки постоянно сталкивались с необходимостью делить продукты, добычу, делать запасы впрок. Таким образом, человек научился считать, производить вычисления. Для счёта использовали пальцы рук, ног, различные предметы.

Например, индейцы изображали числа с помощью узелков на верёвках. Первым способом  «записи» чисел были зарубки на палке. В Древнем Вавилоне записывали числа, выдавливая значки палочкой на глиняной дощечке. В конце-концов были придуманы цифры.

Люди научились складывать и вычитать, затем умножать и делить, причём способы вычислений не всегда были и остаются удобными и понятными.

Большинство обучающихся и взрослых испытывают затруднения при выполнении вычислений. Многие неоправданно часто используют калькулятор, а вот устно же считать почти никто не умеет. Приёмам рациональных вычислений в учебной литературе уделяется крайне мало внимания. При этом, например, сдача ЕГЭ и ГИА предполагает наличие у учеников умений и навыков рациональных вычислений.

Предлагаю вниманию читателя выдержки из проекта «Приёмы быстрого счёта» ученицы 5-А класса новосмолинской МАОУ СОШ №48 Милены Кандыбовой, в которых описаны удобные методы рациональных устных вычислений:

Проект «Приёмы быстрого счёта»Презентация к проектуПродукт проекта

На основе данного проекта в 5-х и 11-м классах новосмолинской МАОУ СОШ №48 были проведены занятия на соответствующую тему, фоторепортажи которых доступны в статьях «Занятие в 5 классах «Приёмы быстрого счёта»» и «Занятие в 11 классе «Приёмы быстрого счёта»».

Умножение и деление на 4

Чтобы число умножить на , его дважды удваивают.

Например:

Чтобы число разделить на , его дважды делят на два.

Например:

Умножение и деление на 5, 50, 500…

Чтобы число умножить на нужно умножить его на и разделить на .

Например:

Чтобы разделить число на нужно разделить его на и умножить на .

Например:

Умножение на 25, 250, 2500…

Чтобы число умножить на нужно умножить его на , и полученный результат разделить на (на делятся только те числа, у которых две последние цифры представляют собой число, делящееся на ).

Например:

Чтобы выполнить деление числа на и т.д. это число надо разделить на и т.д. и умножить на .

Например:

Умножение на 125, 1250, 12500,…

Чтобы число умножить на надо это число разделить на и умножить на . (На делятся только те числа, у которых три последние цифры выражают число, делящееся на ).

Например:

Чтобы число разделить на надо это число разделить на и умножить на .

Например:

Чтобы умножить число на нужно к исходному числу прибавить его половину.

Например:

Чтобы умножить число на , к нему приписывают и отнимают исходное число.

Например:

Умножение двухзначного числа на 111

Умножим на . Мысленно раздвигаем цифры первого сомножителя (), предварительно найдя сумму его цифр: , и вставляем полученную сумму, повторив эту операцию дважды.

Например:

Возведение в квадрат числа, оканчивающегося цифрой 5

Чтобы возвести в квадрат число, оканчивающегося цифрой (например, ), умножают число его десятков () на число десятков, увеличенное на (на ), и к полученному числу приписывают .

Например:

В продолжение темы приёмов быстрого счёта рекомендую прочесть книгу «Магия чисел. Моментальные вычисления в уме и другие математические фокусы», русский перевод которой увидел свет в 2015 году. В аннотации к книге сказано: «Эта книга научит вас считать в уме быстрее, чем на калькуляторе, запоминать большие числа и получать от математики удовольствие.

Любой человек может умножать, делить, возводить в степень и производить другие операции над большими числами в уме и с большой скоростью. Для этого не нужно решать десятки тысяч примеров и учиться годами — достаточно использовать простые приемы, описанные в этой книге. Они доступны для людей любого возраста и любых математических способностей.

Эта книга предназначена для всех, кто любит математику, и для тех, кто хочет научиться молниеносно производить в уме любые вычисления».

Подробные библиографические данные книги доступны в каталоге «Библиотеки Татьяны Мельничук».

Вернуться назад…

МЕТКИ >быстрый счёт, вычисления, математика

Популярные методы устного умножения

Сегодня существует сразу несколько способов умножения в уме. Они не универсальны, но позволяют достаточно успешно производить операции с двузначными числами. Чтобы подобрать для себя оптимальный, лучше ознакомиться с самыми популярными из них:

Вариант 1. Умножение в столбик

Этот вариант отлично подходит тем, кто способен хорошо запоминать и удерживать в памяти сразу несколько промежуточных результатов вычислений. Благодаря этому подходу можно легко производить операции между двузначными числами. Рассмотрим данный вид счета на примере выражения 34*63.

Сначала необходимо умножить 34 на единицы второго числа: 34*3=102. Запоминаем это значение. Затем повторяем операцию уже с десятками множителя: 34*60=2040. Теперь требуется просто сложить результаты наших вычислений: 102+2040=2142

Вариант 2. Умножение с разложением на десятки и единицы

Этот вариант также требует хорошей памяти. Рассмотрим его на примере прошлого выражения 34*63.

Сначала требуется разложить числа на десятки и единицы, у нас получится: (30+4)*(60+3). Далее мы перемножаем между собой десятки: 30*60=1800. Запоминаем этот результат. Затем необходимо умножить десятки первого значения на единицы второго и наоборот: (30*3)+(60*4)=330. Теперь наступает самая сложная часть, главное – не сбиться. Нам нужно сложить результаты наших первых двух примеров и прибавить к ним произведение единиц перемножаемых чисел. Получится следующее выражение: 1800+330+4*3=2142.

Вариант 3. Умножение с большими числами

Этот вид вычислений больше подходит для тех двузначных чисел, которые близки к 100. Рассмотрим этот способ на примере выражения 88*95.

Сначала нужно представить каждое из этих значений как разность 100 и другого числа: 100-a=88 и 100-b=95, a=12, b=5. Так у нас получится (100-12)*(100-5). Теперь нужно произвести следующие вычисления: 88-b и 95-a, 88-5 и 95-12, получится 83 в обоих случаях. Это значение нужно запомнить. Теперь нам нужно найти a*b=12*5=60. Наш итоговый ответ будет состоять из четырех цифр от полученных ранее ответов: 83 и 60, получается 8360.

Иногда в результате подсчетов получается, что второе итоговое значение имеет три знака, а не два. Допустим, у нас получились числа 12 и 345. В этом случае нужно сложить вторую и третью цифру так, чтобы получилось 1545.

Это основные методы устного умножения. Но можно ли их назвать простыми? Несмотря на то, что при усердных тренировках удастся освоить любой из этих подходов, все же они будут требовать хорошей памяти и высокой концентрации. К тому же, не всегда допустимо проводить операции с многозначными числами с помощью данных методов. Лучше постараться найти для себя другие, более простые способы счета.

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей, которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

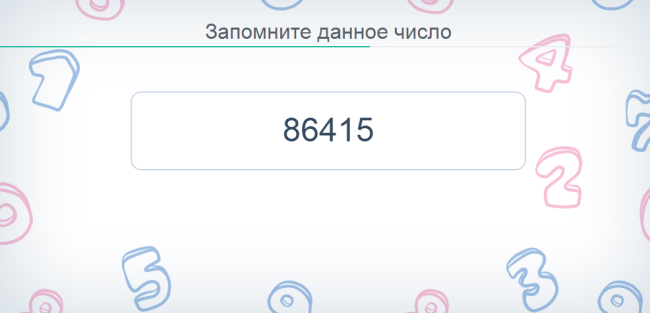
Игра «Числовой охват»

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические сравнения»

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Как умножать на 11?

Чтобы быстро умножать на 11, существует специальный метод, который позволяет выполнять вычисления даже с очень большими числами. Но нагляднее всего этот способ можно продемонстрировать при умножении на 11 двухзначного числа. Поверьте: все – очень просто!

Итак, рассмотрим методику, как умножать на 11.

Запомним правило: чтобы умножить любое двухзначное число на 11, нужно сложить первую и последнюю цифры этого числа, а результат (сумму) вписать посередине (между первой и последней цифрами).

Запомним правило: чтобы умножить любое двухзначное число на 11, нужно сложить первую и последнюю цифры этого числа, а результат (сумму) вписать посередине (между первой и последней цифрами).

Примеры:

Умножим на 11 число 15.

Порядок действий следующий:

• Цифры 1 и 5 пишем с пробелом: 1_5
• Складываем 1 и 5: 1 + 5 = 6.
• Цифру 6 вписываем между единичкой и пятеркой: получаем 165. То есть, 15 х 11 = 165.

Еще пример: умножим 23 на 11:

2_3

• 2 + 3 = 5
• ответ: 253.

Об этой статье

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 87 человек(а). Количество просмотров этой статьи: 15 033.

Категории: Математика

English:Do Long Multiplication

Français:faire une longue multiplication

Español:hacer multiplicaciones largas

Português:Fazer Multiplicações Grandes

中文:计算长乘法

Nederlands:Grote getallen vermenigvuldigen

Bahasa Indonesia:Menyelesaikan Perkalian Panjang

العربية:أداء القسمة المطولة

हिन्दी:बड़ी संख्याओं का गुणा करें

Tiếng Việt:Thực hiện Phép nhân dài

日本語:桁数の多い数字のかけ算をする

ไทย:คูณเลข

한국어:큰 숫자를 곱하는 방법

Čeština:Jak násobit velká čísla pod sebou

Türkçe:Uzun Çarpma İşlemi Nasıl Yapılır

Печать

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения.Давайте рассмотрим задачи на умножение уровня второго класса:

Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Развитие памяти и внимания у ребенка 5-10 лет

Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать. После прохождения курса ребенок сможет:

После прохождения курса ребенок сможет:

1. В 2-5 раз лучше запоминать тексты, лица, цифры, слова
2. Научится запоминать на более длительный срок
3. Увеличится скорость воспоминания нужной информации

Супер-память за 30 дней

Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Сокращенная таблица умножения до 20

1 x 1 = 11 x 2 = 21 x 3 = 31 x 4 = 41 x 5 = 51 x 6 = 61 x 7 = 71 x 8 = 81 x 9 = 91 x 10 = 10 2 x 1 = 22 x 2 = 42 x 3 = 62 x 4 = 82 x 5 = 102 x 6 = 122 x 7 = 142 x 8 = 162 x 9 = 182 x 10 = 20 3 x 1 = 33 x 2 = 63 x 3 = 93 x 4 = 123 x 5 = 153 x 6 = 183 x 7 = 213 x 8 = 243 x 9 = 273 x 10 = 30 4 x 1 = 44 x 2 = 84 x 3 = 124 x 4 = 164 x 5 = 204 x 6 = 244 x 7 = 284 x 8 = 324 x 9 = 364 x 10 = 40 5 x 1 = 55 x 2 = 105 x 3 = 155 x 4 = 205 x 5 = 255 x 6 = 305 x 7 = 355 x 8 = 405 x 9 = 455 x 10 = 50
6 x 1 = 66 x 2 = 126 x 3 = 186 x 4 = 246 x 5 = 306 x 6 = 366 x 7 = 426 x 8 = 486 x 9 = 546 x 10 = 60 7 x 1 = 77 x 2 = 147 x 3 = 217 x 4 = 287 x 5 = 357 x 6 = 427 x 7 = 497 x 8 = 567 x 9 = 637 x 10 = 70 8 x 1 = 88 x 2 = 168 x 3 = 248 x 4 = 328 x 5 = 408 x 6 = 488 x 7 = 568 x 8 = 648 x 9 = 728 x 10 = 80 9 x 1 = 99 x 2 = 189 x 3 = 279 x 4 = 369 x 5 = 459 x 6 = 549 x 7 = 639 x 8 = 729 x 9 = 819 x 10 = 90 10 x 1 = 1010 x 2 = 2010 x 3 = 3010 x 4 = 4010 x 5 = 5010 x 6 = 6010 x 7 = 7010 x 8 = 8010 x 9 = 9010 x 10 = 100
11 x 1 = 1111 x 2 = 2211 x 3 = 3311 x 4 = 4411 x 5 = 5511 x 6 = 6611 x 7 = 7711 x 8 = 8811 x 9 = 9911 x 10 = 110 12 x 1 = 1212 x 2 = 2412 x 3 = 3612 x 4 = 4812 x 5 = 6012 x 6 = 7212 x 7 = 8412 x 8 = 9612 x 9 = 10812 x 10 = 120 13 x 1 = 1313 x 2 = 2613 x 3 = 3913 x 4 = 5213 x 5 = 6513 x 6 = 7813 x 7 = 9113 x 8 = 10413 x 9 = 11713 x 10 = 130 14 x 1 = 1414 x 2 = 2814 x 3 = 4214 x 4 = 5614 x 5 = 7014 x 6 = 8414 x 7 = 9814 x 8 = 11214 x 9 = 12614 x 10 = 140 15 x 1 = 1515 x 2 = 3015 x 3 = 4515 x 4 = 6015 x 5 = 7515 x 6 = 9015 x 7 = 10515 x 8 = 12015 x 9 = 13515 x 10 = 150
16 x 1 = 1616 x 2 = 3216 x 3 = 4816 x 4 = 6416 x 5 = 8016 x 6 = 9616 x 7 = 11216 x 8 = 12816 x 9 = 14416 x 10 = 160 17 x 1 = 1717 x 2 = 3417 x 3 = 5117 x 4 = 6817 x 5 = 8517 x 6 = 10217 x 7 = 11917 x 8 = 13617 x 9 = 15317 x 10 = 170 18 x 1 = 1818 x 2 = 3618 x 3 = 5418 x 4 = 7218 x 5 = 9018 x 6 = 10818 x 7 = 12618 x 8 = 14418 x 9 = 16218 x 10 = 180 19 x 1 = 1919 x 2 = 3819 x 3 = 5719 x 4 = 7619 x 5 = 9519 x 6 = 11419 x 7 = 13319 x 8 = 15219 x 9 = 17119 x 10 = 190 20 x 1 = 2020 x 2 = 4020 x 3 = 6020 x 4 = 8020 x 5 = 10020 x 6 = 12020 x 7 = 14020 x 8 = 16020 x 9 = 18020 x 10 = 200

Первый способ — раскладка на десятки и единицы

Самым простым для понимания способом умножения двузначных чисел является тот, которому нас научили в школе. Он заключается в разбиении обоих множителей на десятки и единицы с последующим перемножением получившихся четырех чисел. Этот метод достаточно прост, но требует умения удерживать в памяти одновременно до трех чисел и при этом параллельно производить арифметические действия.

Например: 63*85 = (60+3)*(80+5) = 60*80 + 60*5 +3*80 + 3*5=4800+300+240+15=5355

Проще такие примеры решаются в 3 действия. Сначала умножаются десятки друг на друга. Потом складываются 2 произведения единиц на десятки. Затем прибавляется произведение единиц. Схематично это можно описать так:

• Первое действие: 60*80 = 4800 — запоминаем
• Второе действие: 60*5+3*80 = 540 — запоминаем
• Третье действие: (4800+540)+3*5= 5355 — ответ

Для максимально быстрого эффекта потребуется хорошее знание таблицы умножения чисел до 10, умение складывать числа (до трехзначных), а также способность быстро переключать внимание с одного действия на другое, держа предыдущий результат в уме. Последний навык удобно тренировать путем визуализации совершаемых арифметических операций, когда вы должны представлять себе картинку вашего решения, а также промежуточные результаты

Вывод.
Не трудно убедиться в том, что этот способ не является самым эффективным, то есть позволяющим при наименьших действиях получить правильный результат

Следует принять во внимание другие способы