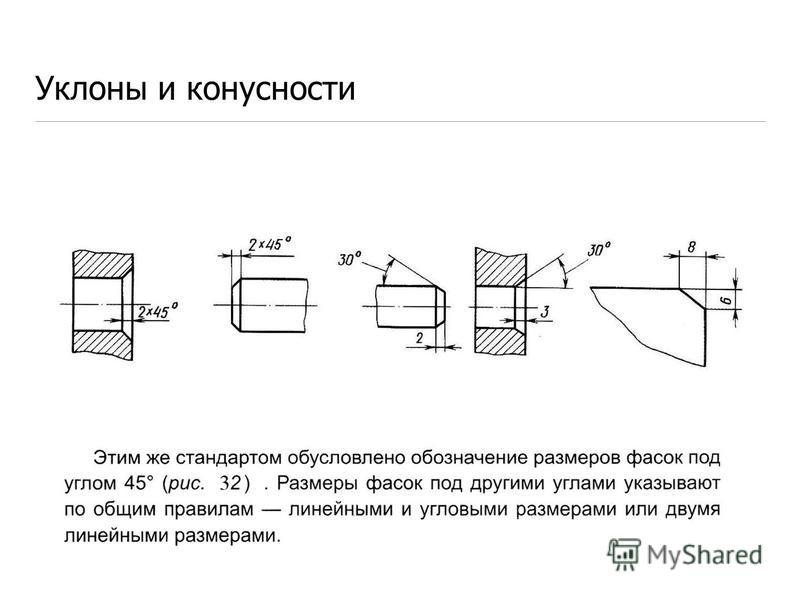
Как нарисовать цилиндр карандашом

Эллипсоид. Сфера и шар

Каноническое уравнение эллипсоида в прямоугольной системе координат имеет вид , где  – положительные числа (полуоси эллипсоида), которые в общем случае  различны. Эллипсоидом называют как поверхность, так и тело, ограниченное данной поверхностью. Тело, как многие догадались, задаётся неравенством  и координаты любой внутренней точки (а также любой точки поверхности) обязательно удовлетворяют этому неравенству. Конструкция симметрична относительно координатных осей и координатных плоскостей:
Происхождение термина «эллипсоид» тоже очевидно: если поверхность «разрезать» координатными плоскостями, то в сечениях получатся три различных (в общем случае) эллипса. В зависимости от значений  эллипсоид может быть вытянут вдоль любой оси, причём вытянут достаточно далеко.

Если две полуоси совпадают, то данную поверхность/тело называют эллипсоидом вращения. Так, например, эллипсоид  получен вращением эллипса  вокруг оси  (представьте мысленно).

Небольшая задачка для самостоятельного решения:

Пример 13

Построить эллипсоид . Записать уравнение порождающего эллипса и ось, вокруг которой осуществляется его вращение.

Чертёж и краткий комментарий в конце урока.

В случае равенства всех полуосей , эллипсоид вырождается в сферу:  – данное уравнение задаёт сферу с центром в начале координат радиуса .

Тело, ограниченное сферой, называется шаром. Неравенство  определяет шар с центром в начале координат радиуса . И, соответственно, противоположному условию  удовлетворяют координаты любой внешней точки.

Разделаемся с аппетитным Колобком:

Пример 14

Построить поверхность . Найти функции, задающие верхнюю и нижнюю полусферу, указать их области определения. Записать аналитическое выражение шара, ограниченного данной сферой и проверить, принадлежат ли ему точки

Решение: уравнение  задаёт сферу с центром в начале координат радиуса 2.  Здесь, как и в примерах с параболическими цилиндрами, выгодно уменьшить масштаб чертежа:
Выразим «зет»: – функция, задающая верхнюю полусферу; – функция, задающая нижнюю полусферу.

Областью определения каждой функции является круг  с центром в начале координат радиуса 2 (проекция полусфер на плоскость ).

Неравенство  определяет шар с центром в начале координат радиуса 2. Подставим координаты точек  в данное неравенство:

1)

Получено неверное неравенство, следовательно, точка «дэ» лежит вне шара.

2)

Получено верное неравенство, значит, точка «эф» принадлежит шару, а конкретнее – его границе (сфере).

Материал о сферах и шарах достаточно прост, и я предлагаю вам чисто символическое задание для самостоятельного решения:

Пример 15

Найти область определения функции двух переменных  и построить соответствующую поверхность.
Краткое решение и чертёж в конце урока.

Кстати, наша планета, кто не знает, чуть-чуть, но таки не шар.

Проецирование точки

Подробности

Категория: Основы начертательной геометрии

 ПРОЕЦИРОВАНИЕ ТОЧКИ НА ДВЕ ПЛОСКОСТИ ПРОЕКЦИЙ

https://vk.com/video_ext.php

Образование отрезка прямой линии АА₁   можно представить как результат перемещения точки А в какой-либо плоскости Н (рис. 84, а), а образование плоскости — как перемещение отрезка прямой линии АВ (рис. 84, б).

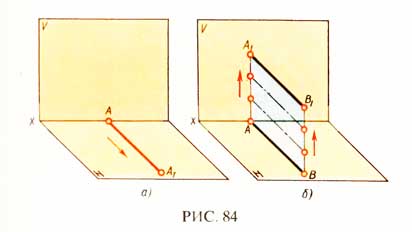Точка — основной геометрический элемент линии и поверхности, поэтому изучение прямоугольного проецирования предмета начинается с построения прямоугольных проекций точки.В пространство двугранного угла, образованного двумя перпендикулярными плоскостями — фронтальной (вертикальной) плоскостью проекций V и горизонтальной плоскостью проекций Н, поместим точку А (рис. 85, а).Линия пересечения плоскостей проекций    — прямая, которая называется осью проекций и обозначается буквой    х.Плоскость V здесь изображена в виде прямоугольника, а плоскость Н — в виде параллелограмма. Наклонную сторону этого параллелограмма обычно проводят под углом 45° к его горизонтальной стороне. Длина наклонной стороны берется равной 0,5 ее действительной длины.Из точки А опускают перпендикуляры на плоскости V и Н. Точки а’и а пересечения перпендикуляров с плоскостями проекций V и Н являются прямоугольными проекциями точки А. Фигура Ааа_ха’ в пространстве — прямоугольник. Сторона аах этого прямоугольника на наглядном изображении уменьшается в 2 раза.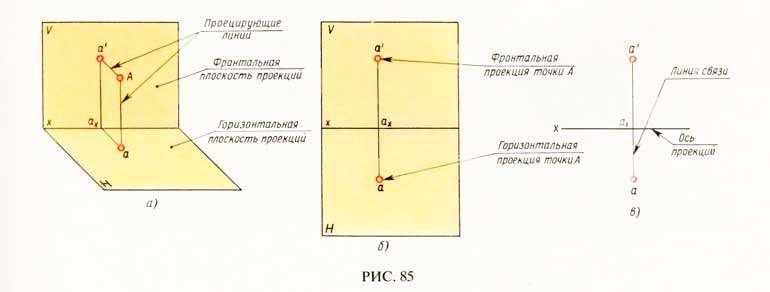

Совместим плоскости Н с плоскостью V ,вращая V вокруг линии пересечения плоскостей х. В результате получается комплексный чертеж точки А (рис. 85, б)

Для упрощения комплексного чертежа границы плоскостей проекций V и Н не указывают (рис. 85, в).Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий — точки а и а’ — называются проекциями точки А: а’ — фронтальная проекция точки А, а — горизонтальная проекция точки А.

Линия а’ а называется вертикальной линией проекционной связи.Расположение проекции точки на комплексном чертеже зависит от положения этой точки в пространстве.

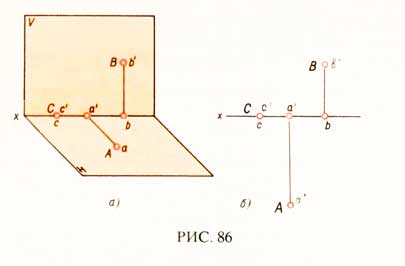Если точка А лежит на горизонтальной плоскости проекций Н (рис. 86, а), то ее горизонтальная проекция а совпадает с заданной точкой, а фронтальная проекция а’ располагается на оси При расположении точки В на фронтальной плоскости проекций V ее фронтальная проекция совпадает с этой точкой , а горизонтальная проекция лежит на оси х. Горизонтальная и фронтальная проекции заданной точки С, лежащей на оси х, совпадают с этой точкой. Комплексный чертеж точек А, В и С показан на рис. 86, б.

ПРОЕЦИРОВАНИЕ ТОЧКИ НА ТРИ ПЛОСКОСТИ ПРОЕКЦИЙ

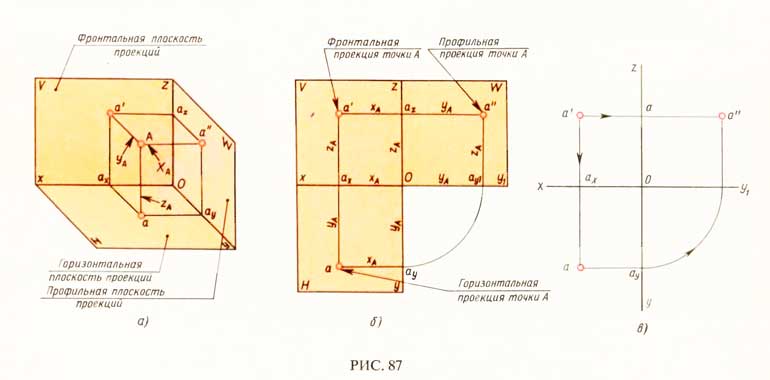
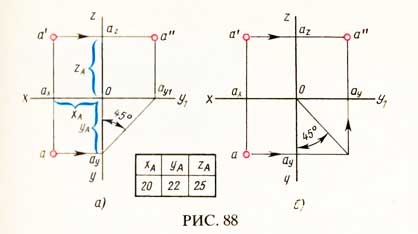
Отрезки проецирующих линий от точки А до плоскостей проекций называются координатами точки А и обозначаются: х_А,    у_А и   z_A.Например, координата z_A точки А, равная отрезку а’а_х (рис. 88, а и б), есть расстояние от точки А до горизонтальной плоскости проекций Н. Координата у точки А, равная отрезку аа_х, есть расстояние от точки А до фронтальной плоскости проекций V. Координата х_А, равная отрезку аа_у — расстояние от точки А до профильной плоскости проекций W.Таким образом, расстояние между проекцией точки и осью проекции определяют координаты точки и являются ключом к чтению ее комплексного чертежа. По двум проекциям точки можно определить все три координаты точки.Если заданы координаты точки А (например, х_А=20 мм,    у_А=22мм и z_A= 25 мм), то можно построить три проекции этой точки.

Для этого от начала координат О по направлению оси Oz откладывают вверх координату z_A и вниз координату у_А.Из концов отложенных отрезков — точек a_z и а_у (рис. 88, а) — проводят прямые, параллельные оси Ох, и на них откладывают отрезки, равные координате х_А. Полученные точки а’ и а — фронтальная и горизонтальная проекции точки    А.По двум проекциям а’ и а точки А построить ее профильную проекцию можно тремя способами:

1)    из начала координат О проводят вспомогательную дугу радиусом Оа_у, равным координате    (рис. 87, б и в), из полученной точки а_у1 проводят прямую, параллельную оси Oz, и откладывают отрезок, равный z_A;2)    из точки а_у проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, а), получают точку а_у1 и т. д.;3)    из начала координат О проводят вспомогательную прямую под углом 45° к оси Оу (рис. 88, б), получают точку а_у1 и т. д.

Поэтапный рисунок горизонтального цилиндра

Разобравшись с падающей теменью, давайте, наконец, нарисуем цилиндр. Для этого слепите его из бумаги, если не нашли подходящего цилиндра в доме. Большая банка из под кофе – прекрасный цилиндр. Чтобы не отвлекала реклама этикеток, сорвите их или покрасьте в белый цвет.

Положите ваш цилиндр на ровный стол так, чтобы он был развёрнут на 45 градусов и, стало быть, чтобы лежал горизонтально. Приступим к рисованию:

1. Начинаем с построения четырёхгранной прямоугольной призмы в перспективе. То же что и куб, только подлиннее.
2. Отлично! Вы хорошо усвоили урок построения кубиков в перспективе.
3. Теперь вспоминаем, как вписать окружность в квадрат, построенный в перспективе. Для этого дорисовываем диагонали в наших квадратах и центральные линии.
4. Итак, основания нашего цилиндра готовы. Соединяем крайние верхние точки на полученных окружностях и крайние нижние между собой. Для проверки, если эти линии продолжить до линии горизонта, то они должны сойтись в точке схода.
5. Для лучшего закрепления материала, строим линейный каркас нашего цилиндра в воздушной перспективе. Усиливаем резкость ближних частей, а дальние приглушаем.
6. Стираем линии построения.
7. Приступаем к построению падающей тени. Попробуйте с фиксированным источником. Закройте окно шторой и включите настольную лампу. Пользуясь советами из предыдущего раздела постройте тень. Для более точной тени от окружности, проводите побольше линий от источника света и от его проекции на стол.
8. Когда тень построена можно приступать к штриховке. Помните! Начинаем с самых тёмных мест, заканчиваем самыми светлыми.

Ну вот, вам покорилась ещё одна гладкая фигура, теперь вы сможете нарисовать не только нос и колпачок Буратино, но и его шею, туловище, ноги, пальцы и многое другое. В следующем уроке до головы доберёмся. Так что оставайтесь с нами!

Законы рисования в угловой перспективе

• Перспектива. Если присмотреться к башне внимательней, можно увидеть, что передний угол пьедестала находится ближе. Это возможно благодаря тому что основание представляет собой трапецию, а не квадрат.
• Расположение. Опять же, нужно посмотреть на пьедестал. Он располагается ближе, чем все остальные части конструкции.
• Размер. Срединная вертикаль – это место, где сходятся направляющие линии. Так как она находится в центре башни, он кажется больше и ближе.
• Перекрытие. Мы не видим задние углы всей башни, потому что они перекрыты передними. Этот приём тоже создаёт эффект объемности фигуры.
• Затенения. Та сторона, которая противоположна свету, рисуется более тёмной. Это создаёт глубину.
• Тени. Без них нарисованный объект парил бы в воздухе. Они делают башню более реалистичной.
• Контур. Все изображение строится на основе контурных линий. С помощью них можно дорисовать любые детали.
• Горизонт. А эта линия является образующей. Благодаря ей мы можем понять расположение глаз рисующего относительно объекта.
• Плотность. С помощью тех же опорных точек можно нарисовать ещё много башен различного размера.

Эти законы обязательно нужно запомнить, чтобы облегчить процесс рисования и сделать его правильным. Сделать это можно при помощи ассоциаций или смешного предложения на начальные буквы каждого слова. Например: “Пушистая рыжая рысь пошла за тем красным говорливым попугаем”

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

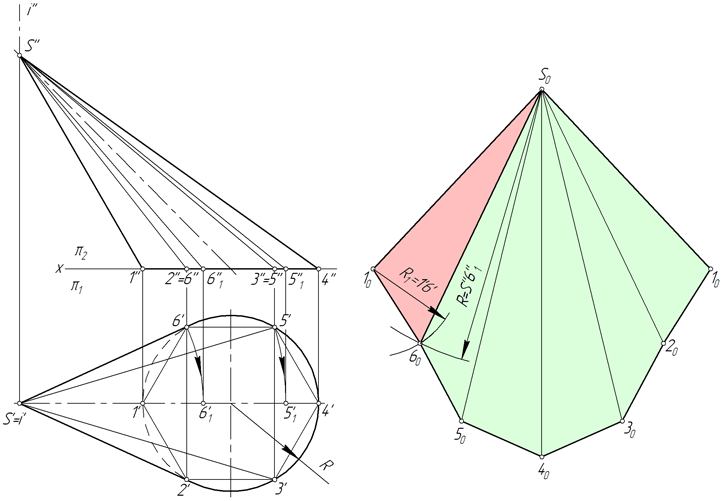
Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

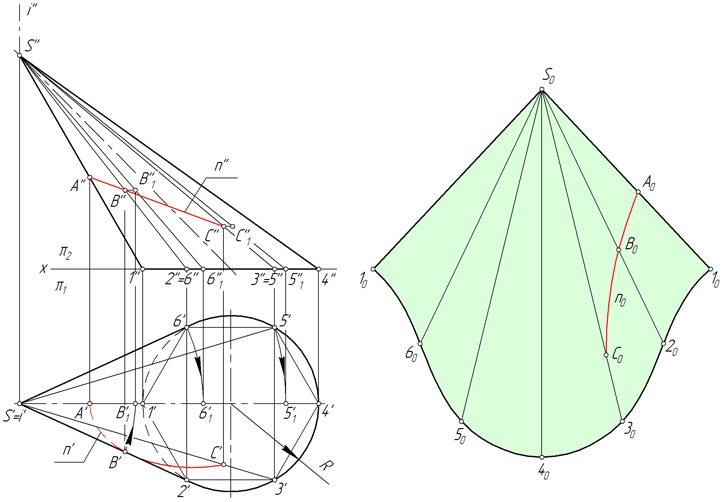
Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, Cплавной линией.

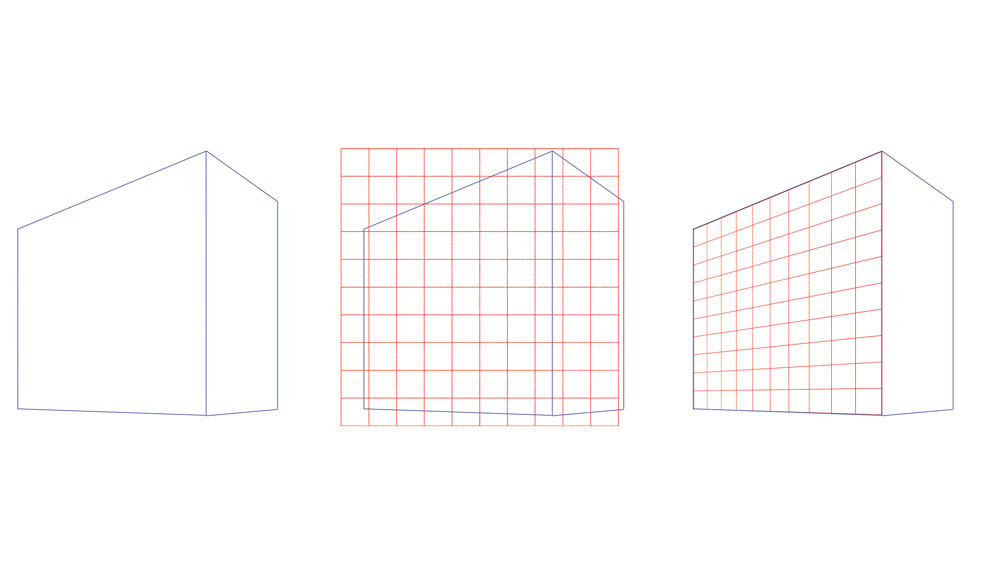
Как нарисовать объемный квадрат с одной точкой перспективы

Немного более продвинутый способ нарисовать объемный квадрат — это использовать перспективу с одной точкой схода. Получившийся объемный квадрат очень похож на тот, который мы рисовали простым способом, разница в том, что он получается чуть более сдавленным за счёт перспективы.

Не смотря на то, что рисовать такой объемный квадрат немного сложнее, результат выглядит намного более реалистично. Вот что делает перспектива, перспектива это отличный способ изобразить объемные объекты на плоской бумаге. Давайте же нарисуем наш объемный квадрат в перспективе!

Шаг 1: Нарисуйте квадрат и точку схода

Как и в первом случае, сначала нарисуйте обычный квадрат.

Затем отметьте точку, в которую будет сливаться наша перспектива. Эта точка называется точкой схода. В нашем примере мы поместили её в правом верхнем углу, таким образом, мы получим вид объемного квадрата, который похож на тот, что мы нарисовали в примере выше.

После того, как вы нарисуете объемный квадрат так, как показано здесь, поиграйте с размещением вашей точки схода. Попробуйте переместить её подальше, вниз или влево, изменение положения точки схода даст вам совершенно другой вид вашего объемного квадрата.

Шаг 2: Обозначьте линии перспективы

Нарисуйте линии перспективы, они послужат ориентирами для будущего объемного квадрата. Они начинаются в двух верхних и правом нижнем углу нашего переднего лицевого квадрата и сливаются в точку схода. (Эта точка называется точкой схода, так как по мере приближения к этой точке все объекты становятся меньше. В точке схода объекты будут настолько малы, что просто исчезнут.)

Чтобы вам было проще и линии получились ровные воспользуйтесь линейкой, это сильно упростить вам задачу.

Кроме того, не прорисовывайте эти линии слишком сильно – они нам нужны только в качестве ориентиров и позже мы их сотрем.

Шаг 3: Нарисуйте дальние грани объемного квадрата

С помощью вспомогательных направляющих линий перспективы, нарисуйте дальние грани объемного квадрата.

Обе линии обозначающие задние грани объемного квадрата должны начинаться и заканчиваться на направляющих линиях перспективы. Сначала нарисуйте верхнюю дальнюю грань параллельно (в том же направлении) горизонтальной верхней линии передней грани квадрата.

Затем аналогично нарисуйте вертикальную (сверху вниз) дальнюю грань.

Да, вот несколько причудливых слов, которые вы только что узнали:

• «Параллельные» линии — это две линии, идущие в одном направлении.
• «Вертикальная» линия — это линия, идущая сверху вниз или снизу вверх.
• «Горизонтальная» линия — это линия, идущая слева направо или справа налево, такая же как и горизонт.
• А «горизонт» — это линия, где земля встречается с небом, если смотреть вдаль – линия, которая проходит ровно слева направо.

Шаг 4: Нарисуйте боковые грани, чтобы завершить объемный квадрат

После короткого лингвистического отступления мы возвращаемся к рисованию объемного квадрата.

Следующий шаг очень простой – просто дорисуйте грани объемного квадрата проведя карандашом по вспомогательным линиям перспективы соединив его переднюю и заднюю стороны.

Шаг 5: Сотрите вспомогательные линии

Последний этап состоит в том, чтобы стереть точку схода и вспомогательные линии, которые вы нарисовали раньше.

Как вы можете заметить, полученный рисунок объемного квадрата очень похож на простой способ, который мы использовали выше, только немного более приплюснутый сзади. Но именно это делает его более реалистичным, и он выглядит как настоящий куб в трёхмерном пространстве, хотя он и нарисован на плоской бумаге.

Построение цилиндра в перспективе, вид сбоку.

Положим один кирпич поверх другого. Предположим, что их торцы образуют
квадрат. Нарисуем на торцах диагонали и тем самым найдем центр. Это центр
круга, который касается всех четырех сторон квадрата.

Рис. 13.11. Построение цилиндра в черчении без
перспективы.

Этот круг можно расценивать как торец цилиндра, который проходит через всю
толщу кирпича. На противоположном торце нарисуем еще один круг.

Линия, проведенная между центрами двух окружностей, — это центральная/осевая
линия цилиндра или в нашем случае — ось двух колес. Эта ось — продолжение
коротких осей двух эллипсов и ножка двух букв Т.

Длинная ось образует перекладину буквы Т.

Мы начали с предположения, что торцы двух кирпичей, положенных один на
другой, образуют квадрат.

Теперь попробуем рисовать цилиндр в
перспективе.

Нарисуем кирпичи с применением законов перспективы. Круг, вписанный в
квадрат, становится эллипсом, касающимся сторон квадрата (нарисованного в
перспективе) в центре каждой из сторон.

Рис. 13.12. Построение цилиндра в перспективе.

Линия, проведенная через центр круга до точки схода, должна быть центральной
линией цилиндра или осью для двух колес.

Линия, проведенная через этот же центр и пересекающая эту ось под прямым
углом, будет самой длинной линией или большой осью эллипса.

Большая ось всегда образует прямой угол с центральной осью цилиндра.

Нет никакой разницы, в каком направлении лежит цилиндр и лежит ли он на боку
или стоит на торце, большая ось эллипса всегда будет образовывать букву Т с
центральной/осевой линией цилиндра. Малая ось эллипса лежит вдоль этой
центральной/осевой линии цилиндра. Малая ось эллипса становится центральной
линией цилиндра, т.е. они должны совпадать.

Рис. 13.13. Правильное положение осей эллипса цилиндра в пространстве.

Нарисуйте/начертите цилиндр с соблюдением правил перспективы. Затем
поверните бумагу так, чтобы цилиндр оказался в вертикальном положении.

Рис. 13.14. Цилиндр в перспективе в вертикальном положении.

Первое изображение цилиндра является правильным, второе — неправильное.

Перспектива в художественных произведениях

Анализ наброска с натуры городского пейзажа

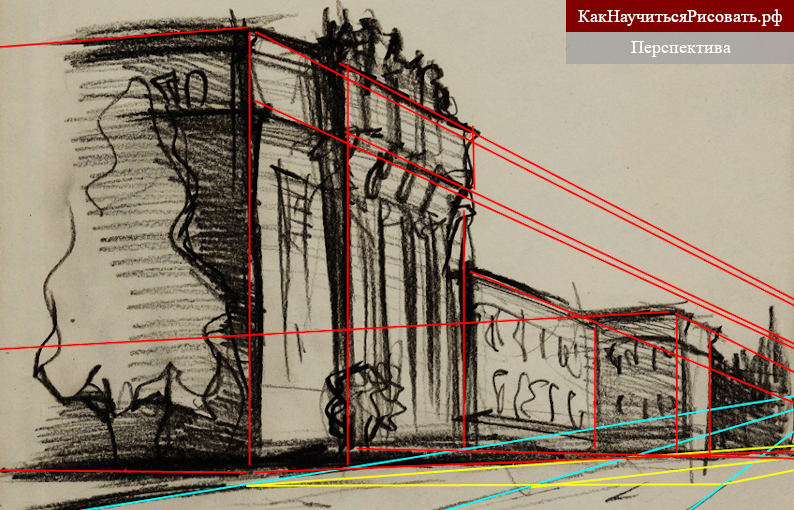
На представленном наброске городского пейзажа изображено здание Театра оперы и балета на площади. Здание достаточно большое и на нем великолепно просматриваются перспективные сокращения его размеров. Площадь, имеет возвышенность, на которой расположен театр. Поэтому линии, обозначающие дорожную разметку имеют на разных участках различные линии перспективы и точки схода этих линий.

Анализ натюрморта

Анализируемый натюрморт имеет очень сложную с точки зрения перспективы структуру. В натюрморте представлены как горизонтально расположенные объекты с прямоугольными основаниями, так и наклоненный цилиндр с увенчивающим его призматическим объектом с квадратным основанием.

Перспектива цилиндра

Построим
перспективу цилиндра, стоящего на
горизонтальной плоскости:

1.
Строим перспективу квадрата, в который
вписываем по восьми точкам эллипс —
нижнее основание цилиндра.

2.
Строим перспективу квадрата, в который
вписываем верхнее основание цилиндра.

Рис. 3.5. Перспектива
прямого цилиндра, стоящего на
горизонтальной плоскости.

Построим
перспективу горизонтально лежащего
цилиндра, расположенного под углом к
картине.

1. При
   совмещенной точке зрения откладываем
   угол в натуральном размере. Продляем
   его стороны до пересечения с линией
   горизонта, получаем точки схода
   F₁
   и F_2.

2. Строим
   перспективу вертикально расположенного
   квадрата ABCE.
   Точка схода для сторон квадрата — F_1.

3. Проводимгоризонталь
   из точки А и откладываем на ней длину
   цилиндра: на оси ОХ откладываем значение,
   равное координате Х точки А плюс длина
   цилиндра, из полученной точки откладываем
   луч в Р. В точке пересечения луча и
   горизонтали – точка 1. Из точки 1 проводим
   луч в f_1.
   

4. Из
   точек А, B, C, E проводим лучи в точку схода
   F₂.
   В пересечении А
   F₂
   и
   1f_{1
   —} точка
   G – точка квадрата, в который вписано
   верхнее основание цилиндра.

5. Проводим
   из точки G лучи в точки схода F₁
   и F_2.

6. Строим
   перспективу квадрата GJL
   К, в который вписано верхнее основание
   цилиндра.

7. Вписываем
   окружности в квадраты
   ABCE и GJLК.

Рис. 3.6. Перспектива
горизонтально лежащего цилиндра,
расположенного под углом к картине.

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

7.9. Пересечение прямой с поверхностью конуса

Пусть задан прямой круговой конус и прямая общего положения m (Рисунок 7.14). Найти точки «входа» и «выхода» прямой с поверхностью конуса.

1. Через прямую m проводим вспомогательную секущую плоскость σ, дающую в сечении наиболее простую фигуру.
2. Применение в качестве вспомогательной секущей плоскости проецирующей плоскости в данном случае нецелесообразно, так как в сечении получится кривая второго порядка, которую нужно строить по точкам.

Наиболее простая фигура – треугольник. Для этого секущая плоскость σ должна пройти через вершину S. Плоскость зададим с помощью двух пересекающихся прямых σ=SM∩MN или, что, то же самое,  (σ=SM∩m).

1. Возьмем на прямой m точку А и соединим её с вершиной. Прямая SA пересечёт плоскость основания в точке М.
2. Построим горизонтальные проекции этих объектов.
3. Продлим фронтальную проекцию прямой m до пересечения с плоскостью основания в точке N.

Рисунок 7.14 – Построение точек пересечения прямой с поверхностью конуса

1. Построим её горизонтальную проекцию.
2. Соединим точки M₁N₁, на пересечении с окружностью основания получим точки 1 и 2.
3. Строим треугольник сечения конуса плоскостью σ, соединив точки 1 и 2 с вершиной S.
4. На пересечении образующих 1-S и 2-S с прямой m получим искомые точки K и L.
5. Определим видимость прямой относительно поверхности конуса.

На анимации ниже представлена последовательность построения точек пересечения прямой с поверхностью конуса.

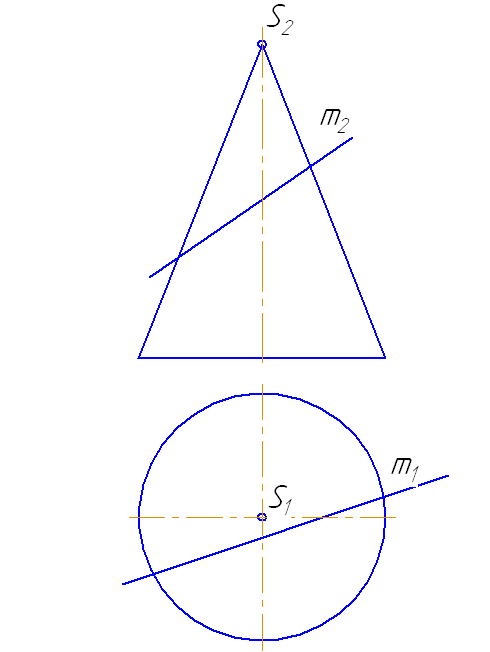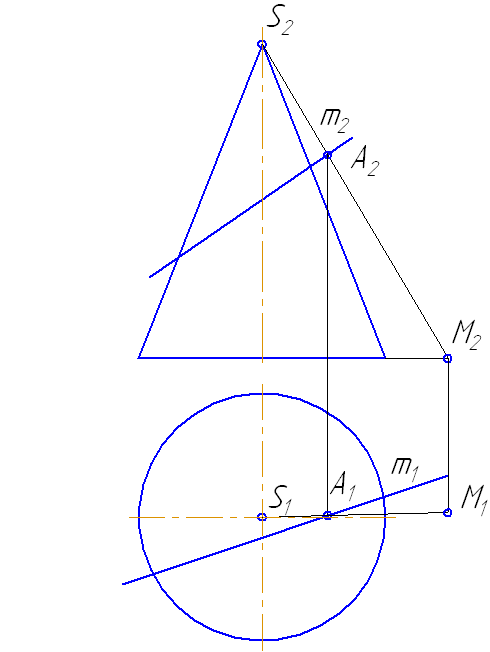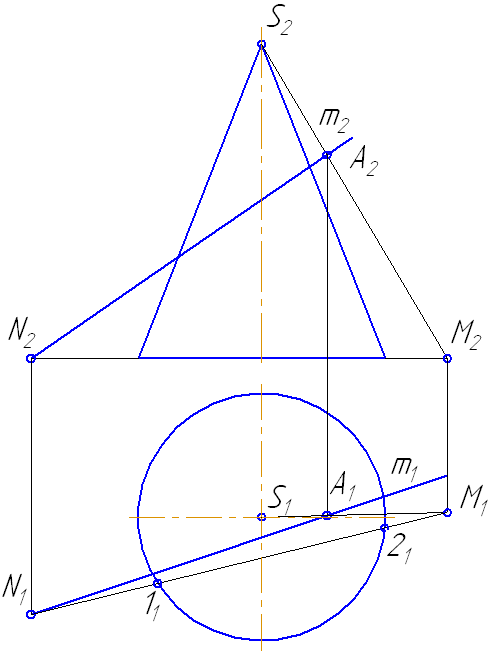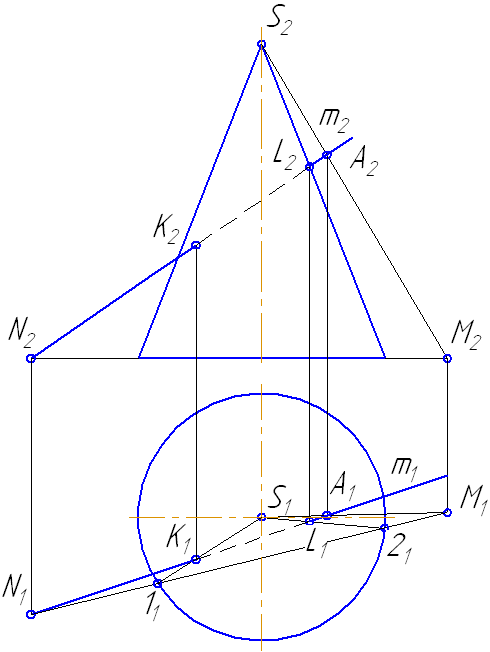
7.12. Пересечение конуса плоскостью

Рассмотрим пять возможных вариантов расположения плоскости относительно поверхности прямого кругового конуса. Пусть плоскость сечения перпендикулярна плоскости проекций π₂ (Рисунок 7.16).

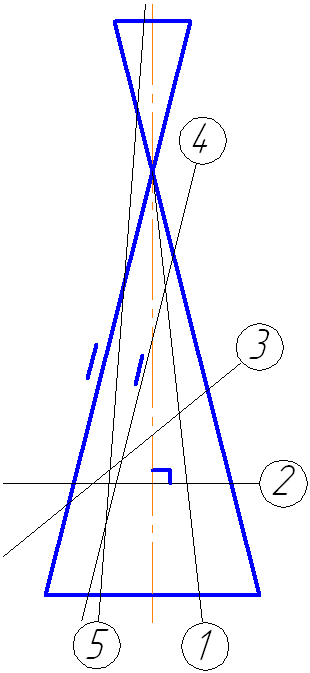
Рисунок 7.16

1. Если плоскость проходит через вершину (1) – в сечении две образующие и прямая пересечения с плоскостью основания.
2. Если плоскость перпендикулярна оси вращения конуса (2) – в сечении окружность.
3. Если плоскость не параллельна ни одной образующей (пересекает все образующие (3)) – в сечении эллипс.
4. Если плоскость параллельна одной образующей конуса – в сечении парабола (на примере – плоскость сечения (4) параллельна крайней образующей конуса).
5. Если плоскость параллельна двум образующим (пересекает обе полости конической поверхности (5)) – в сечении гипербола (рисунок 7.17).

Рисунок 7.17. Плоскость сечения параллельна двум образующим конуса

Ниже, на моделях, представлены варианты положения секущей плоскости относительно поверхности конуса, при которых получаются сечения в виде эллипса, параболы и гиперболы.

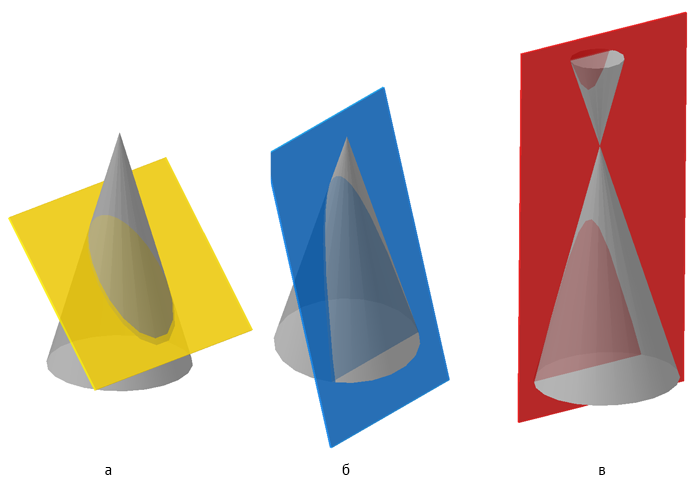
Рисунок 7.18 – Сечение конической поверхности плоскостью (а — эллипс, б — парабола, в — гипербола)

Рассмотрим пример построения сечения конической поверхности плоскостью.

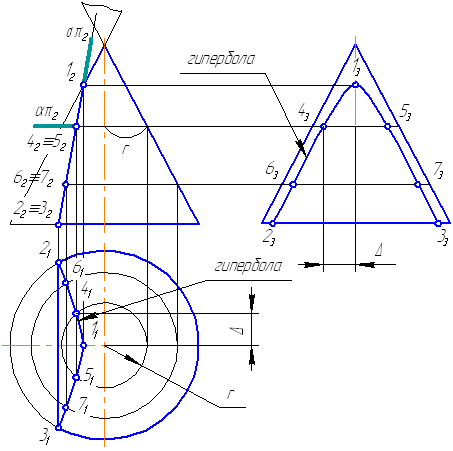
Рисунок 7.19 – Построение пересечения конической поверхности плоскостью

Пусть задана секущая проецирующая плоскость σ⊥π₂ (Рисунок 7.19). Если продлить коническую поверхность и проекцию плоскости, то видно, что плоскость пересекает вторую ветвь конической поверхности, следовательно, в сечении получится гипербола.

1. Построим характерные точки. Это точки, лежащие на крайних образующих и на окружности основания конуса (1, 2, 3). Их проекции строятся по линиям проекционной связи.
2. Для построения промежуточных точек, воспользуемся методом вспомогательных секущих плоскостей. Введём плоскость α⊥π₂ и перпендикулярно оси вращения, что даст в сечении окружность радиусом r. Строим эту окружность на π₁. Плоскость α пересекает и заданную плоскость сечения по прямой, проекции которой на π₁ и π₃ совпадают с линиями проекционной связи.
3. На пересечении этих двух сечений на плоскости проекций π₁ строим точки 4, 5. Профильные проекции этих точек строим по линии проекционной связи, откладывая расстояние от оси вращения конуса, равное Δ.
4. Аналогично строим точки 6, 7. Плавно соединим построенные точки, образуя гиперболу.
5. Обведём то, что осталось от конуса после такого среза с определением видимости. В нашем примере все проекции построенной кривой будут видимы.

На анимации ниже представлена последовательность построения пересечения конической поверхности плоскостью.

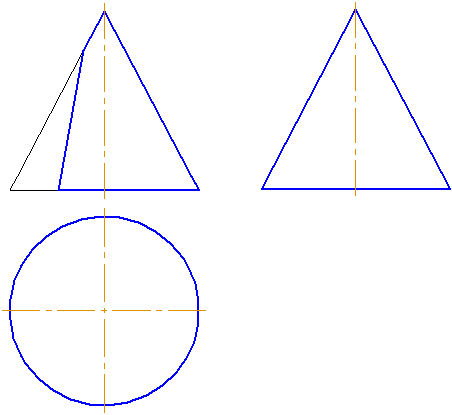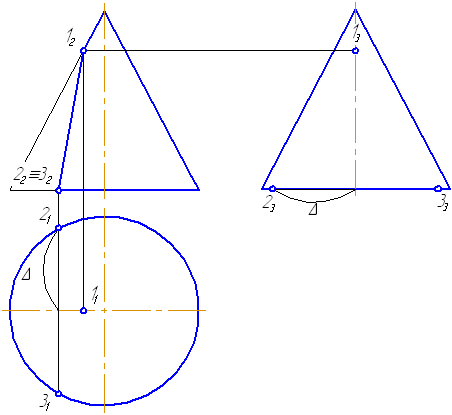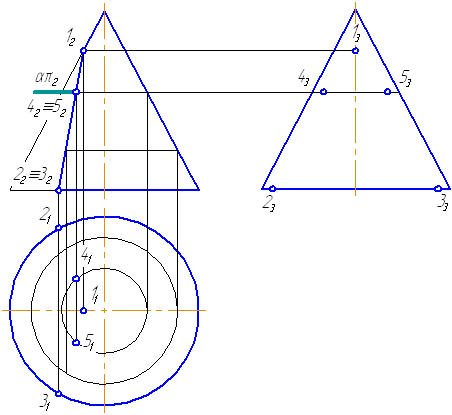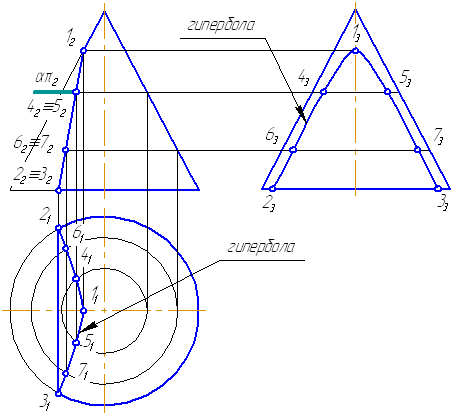
Как построить фронтальную перспективу поэтапно

Для того, чтобы сделать метод понятным и легким, давайте рассмотрим построение фигуры шаг за шагом. В качестве иллюстрации приведем готовый цветной рисунок фронтальной перспективы куба (параллелепипеда).

Фронтальная перспектива куба (параллелепипеда)

Шаг 1 — горизонт и точка схода

На первом этапе мы определяем основные элементы рисунка в перспективе: линию горизонта и точку схода. Технически, оба элемента можно нарисовать где угодно, однако на практике не каждая выбранная позиция будет удачной.

Рисование во фронтальной перспективе

Шаг 2 — линии схода

Теперь нам нужно прочертить две линии схода, которые определят ширину фигуры. Вдоль них будут проходить боковые грани параллелепипеда.

Линии схода

Шаг 3 — основание фигуры

С помощью двух линий схода можно изобразить основание фигуры. Для этого нужно просто провести две горизонтали из одной линии схода в другую. Таким образом мы задаем глубину нашего прямоугольного параллелепипеда. Боковые кромки (левая и правая) получаются простой прорисовкой линий схода между двумя горизонталями.

Основание фигуры

Шаг 4 — вертикальные ребра

Возьмем две угловые точки в ближней к нам части фигуры и нарисуем из них две вертикальные линии вверх. Эти отрезки представляют собой ребра передней грани параллелепипеда.

Вертикальные ребра

Шаг 5 — пересечение верхних линий

На пятом шаге построим еще две линии схода, которые пересекают нарисованные ранее вертикали. Таким образом задается высота параллелепипеда

При этом важно, чтобы два вертикальных ребра были на одной высоте. Проще всего выполнить шаг 5 вместе с шагом 6

Пересечение верхних линий

На этом шаге мы нарисовали все необходимые линии схода. Как вы можете видеть, все они возникают из одной и той же точки схода. Эта особенность одноточечной перспективы и делает этот вид перспективы сравнительно легким.

Шаг 6 — рисуем переднюю грань

Теперь нарисуем переднюю грань фигуры. Для этого две точки пересечения между вертикалями и верхними линиями схода соединяются горизонтальной чертой. Звучит сложнее, чем есть — просто посмотрите на картинку ниже. Горизонтальная черта автоматически приведет к точке пересечения второй линии схода. Мы уже сделали это в пункте 5. Еще можно было бы сделать так: рисуется только одна линия схода, затем горизонтальный верхний край фигуры, а затем вторая линия схода.

Передняя грань

Шаг 7 — дальние вертикальные ребра

На седьмом шаге рисуем еще две вертикальные линии в двух дальних угловых точках основания фигуры. Они представляют собой дальние ребра.

Дальние вертикальные ребра

Новые линии должны быть соединены друг с другом горизонтальным отрезком так же, как на шаге 6.

Задняя грань

Шаг 9 — верхние боковые ребра

Теперь нам осталось только нарисовать верхнюю поверхность фигуры. В одноточечной перспективе это просто прорисовывание верхних линий схода — между двумя верхними горизонтальными ребрами.

Верхние боковые ребра

Шаг 10 — готовый рисунок

Построение фронтальной перспективы параллелепипеда готово. Для того, чтобы получить окончательную фигуру, надо просто стереть ненужные элементы рисунка (линии схода и невидимые ребра). Невидимые ребра изображены светло-серым цветом на рисунке ниже.

Параллелепипед во фронтальной перспективе — финал

Как видите, рисовать в одноточечной перспективе несложно. Конечно, этот пример — очень простое упражнение на рисование фронтальной перспективы. С более замысловатыми объектами сложность возрастает, но, тем не менее, базовые принципы остаются теми же самыми.

Как нарисовать объемный квадрат с двумя точками перспективы

Третий способ нарисовать объемный квадрат — это способ с применением двухточечной перспективы. Он использует аналогичные рекомендации как и для случая с одной точкой перспективы, разница в том, что перспектива сходится в две разные точки. В результате получается очень динамичный и немного преувеличенно-вытянутый вид объемного квадрата, который как будто выскакивает из плоского чертежа в третье измерение.

Шаг 1: Нарисуйте две точки схода

Начнем с простого, отметив две точки схода перспективы.

Нарисуйте горизонтальную линию в верхней части листа бумаги. Затем отметьте две точки по краям, как можно дальше друг от друга. Вот так!

Чем ближе друг к другу вы расположите точки, тем более сплющенным и менее естественным будет выглядеть ваш куб(объемный квадрат), поэтому нарисуйте точки как можно дальше друг от друга, так кую будет выглядеть лучше.

После того как мы закончим рисовать этот вариант объемного куба, вы можете поэкспериментировать и попробовать сместить линию точек схода на листе бумаги вверх или вниз, так же совсем не обязательно чтобы эта линия была строго горизонтальной, её можно нарисовать как угодно, попробуйте, вам понравится!

Шаг 2: Нарисуйте переднюю грань

Следующий этап: нарисуйте прямую вертикальную линию – это будет передняя грань объемного квадрата. Поместите линию в середине листа бумаги, на небольшом расстоянии от горизонтальной направляющей.

Если вы сместите вертикальную линию больше влево, вы увидите больше правой стороны куба. Сместите линию вправо, чтобы увидеть больше левой стороны. Сместите линию вверх и на рисунке вы будете видеть меньше верхней части куба. А если вы проведете линию так,  что она будет пересекать горизонтальную линию, то вы не увидите ни верха, ни низа вашего объемного квадрата. Понимаете, как это работает?

Шаг 3: Нарисуйте линии перспективы

Наметьте четыре линии направления перспектив. Нарисуйте две линии из верхнего края грани нашего будущего объемного квадрата, так чтобы они соединились с точками схода.

Затем аналогично еще две линии из нижней части грани, также к точкам схода. Если у вас есть линейка, нарисуйте эти линии с помощью линейки, желательно чтобы линии получились прямые.

Шаг 4: Нарисуйте боковые грани

Нарисуйте две параллельные вертикальные линии, по одной с каждой стороны. Это левый и правый края объемного квадрата в двухточечной перспективе.

Шаг 5: Нарисуйте направляющие

Теперь, когда у нас есть вертикальные грани нашего Куба, нарисуйте еще две направляющие обозначающие перспективу.

Они начинаются с верхних концов боковых рёбер нашего объемного квадрата. Линия от правого ребра идет к левой точке перспективы. Линия от левого ребра идет к правой точке. Таким образом, линии пересекаются создавая верхнюю сторону объемного квадрата.

Это гораздо легче увидеть на картинке, чем объяснить словами.

Шаг 6: Прорисовываем грани

На этом этапе мы просто более чётко нарисуем все недостающие грани объемного квадрата.

Сначала прорисуйте нижние грани. Затем обведите контуром верхнюю сторону куба — четыре ребра, обозначенные пересекающимися направляющими перспективы.

Шаг 7: Сотрите вспомогательные линии

Это финальный этап. Сотрите все вспомогательные линии перспективы, чтобы полностью очистить ваш рисунок от всего не нужного. Мы также добавили горизонтальную проходящую линию за нашим объемным квадратом — она создаст эффект того, что куб как бы лежит на столе или какой-то другой поверхности.

Вот и все – теперь вы умеете рисовать объемный квадрат в 2-х точечной перспективе. Как видите, результат получился очень даже динамичным и выразительным.

Если вы хотите, чтобы нижний угол выступал меньше и выглядел немного более естественно, просто нарисуйте центральное ребро куба (самую первую вертикальную толстую линию) выше и ближе к горизонту. Ну а дальше все поэтапно начиная с шага №2.

Поделись советом

36 захватывающих фактов о «Титанике»

Как влияет радиация на организм человека?

Как нарисовать лошадь карандашом поэтапно для начинающих

Как запустить жиросжигание в организме?

9 мифов о женском здоровье, которые никогда не умрут

Красная нитка на запястье, что это значит?

Как нарисовать